平面群

壁紙（2次元）の繰り返し模様の対称性は，17種類の平面群に分類されます．17種類の平面群の表を掲載しておきます．それぞれの対称群の説明はこれからするのですが，先にこの表を提示するのも，役に立つことでしょう．
この表で，採用した平面群の表記法は，国際記号とロシア式記号です．(”Симметрия”, Шубников и Копцикより)
今日，国際記号が普及していますが，ロシア式記号は，群の生成元を表示しているので，群の構造が良くわかる特徴がありますから，群の理論的研究に適しています．両者の対応を表にまとめておきます．

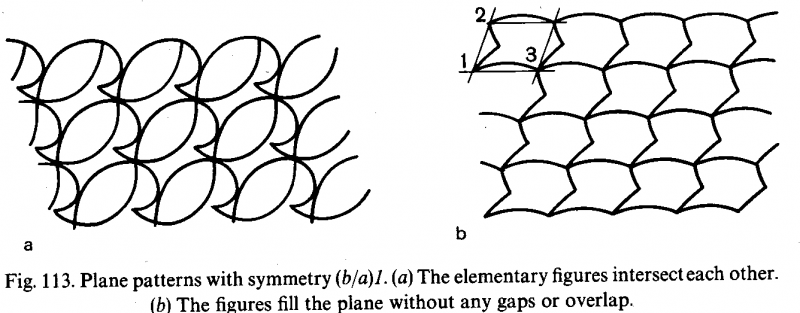
国際記号$$p1$$，ロシア式記号$$(b:a)1$$

対称性が並進（格子の周期）以外に何もないパターンの例です．

 図中に同じ部分が繰り返し出てくる様子を調べます．例えば，上図のような格子が見つかるでしょう．このように格子周期以外の対称性がない場合は，単位胞タイル（オレンジで囲んだ平行４辺形）の中身全部が非対称要素（モチーフ）です．

平面群の記号で，格子を表す部分は，国際記号で$$p$$（なんの条件もない平行４辺形），ロシア式記号で$$(b/a)$$［$$b$$軸と$$a$$軸が直角でない一般的な角度で交差］と表します．点群の対称性の記号は何もないので$$１$$と記載します．

これが，もっとも簡単な平面群（第１類）です．
以下の図のように平行４辺形を変形したものも，この対称性を持っています．

この対称性に属するエッシャーの周期的な作品もいくつかあります．
私は，ハロウイン魔女を作って見ました．

 美しい幾何学p.68

 第2回目（第2類）は，国際記号$$pg$$，ロシア式記号$$( b:a)･\tilde{a}$$の対称性です．
$$g$$はglide plane (映進面)の意味，$$\tilde{a}$$は並進成分が$$a$$軸方向に沿った映進の意味です．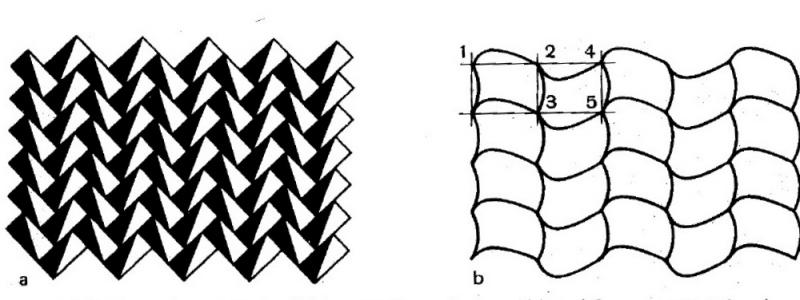  

上図の模様は，どちらも同じ対称性で，横軸方向に映進があります．縦軸（上下方向）方向には映進はありません．

上図は有名なエッシャー作品（邂合）です．この図は縦方向$$b$$軸に沿って，映進$$\tilde{b}$$がありますので$$( b:a)･\tilde{b}$$，先の例を90°回してみたものと同じ対称性に属します．
■映進操作の説明は以下で行います．

美しい幾何学p.93-95

表紙の写真はネットからお借りしたエジプトの模様です．
(今回の対称性は繰り返し模様の第３類）
この対称性は，国際記号で$$p2$$，ロシア式記号で$$(b/a):2$$　と記述されるのもです．作り方は，紙面に垂直な2回回転対称軸が，横軸（水平方向）に配列している状態が基本になります．その1次元の状態は，$$(a):2$$と表示します．周期的に（横軸$$a$$方向に）2回軸（赤で染めている）が1次元配列をしている状態なら，それらの2回軸の中心に新しい2回軸（白抜きにしている）が生じることは，図を見ているとわかるでしょう．

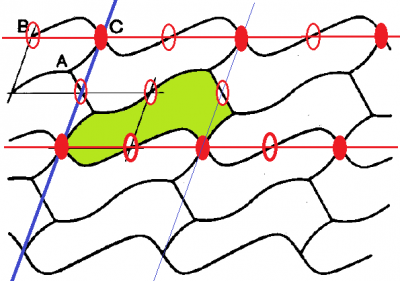
さて，この１次元の帯を，$$b$$軸(青い直線）に沿って繰り返し平行移動して2次元のパターン$$(b/a):2$$が得られます．$$b$$軸と$$a$$軸の交差する角度は，直交とは限りません（一般的な角度でOK）［注）ロシア式記号$$(b/a)$$は一般的な角度の意味．直交する場合は，$$(b:a)$$と書くのが決まりです］．この場合，非対称要素（モチーフ）は単位胞タイルの1/2(例えば黄緑色に着色した部分）です．

この対称性の繰り返し模様はエジプトの模様でよく見られます．私たちも知らず知らずのうちに，このような模様をエジプトの民芸で見ているのでしょう．この模様を見たときなんとなくエジプト風を感じませんか．

表紙の模様もそうですが，次の模様も同様です．

これらのエジプトの模様では，$$b$$軸と$$a$$軸は直交していますが，これはたまたまのことで，軸を直交させたとしても全体の対称性は変わりません（対称性が上昇するわけではないので記号を変える意味がありません）．［注）2回回転対称軸が存在できる格子は，$$a$$軸と$$b$$軸が斜交しているもの（平行4辺形）でかまいません．もちろん直交してもかまわないのですが，条件のゆるい斜交している方を選びます］　次の図は，上のエジプトの模様を私が改造して，一般的な角度で$$b，a$$の軸が交差する模様に変えてみました．対称性は同じです．

今回は，平面群の第４類の説明です．この類は，直交する２つの映進面がありますので複雑です．
映進面が１つのパターン$$pg$$の例を参照ください．

以下のペルシャのパターンが，$$pgg2$$の繰り返し模様の例です．

国際記号で$$pgg2$$，ロシア式記号で$$(b:a):\tilde{b}:\tilde{a}$$と書かれるものです．
［構成方法１］ 
①　2回対称軸が$$a$$軸方向に周期的に配列した1次元構造（図の1番上の行にあります）；　
この対称性は$$(a):2$$
②　この1次元構造を，$$b$$軸（$$a$$軸に垂直）に沿って映進$$\tilde{b}$$すると，2次元のパターンが得られます．　　対称性$$( b:a) :\tilde{b}:\tilde{a}$$
(注) 1次元構造$$( b) :2$$を映進$$\tilde{a}$$で繰り返し広げても同じ構造が得られます．
［構成方法２］
互いに直交する２つの映進面$$\tilde{a}$$，$$\tilde{b}$$が作用すると，
このパターン$$( b:a) :\tilde{b}:\tilde{a}$$が得られます．

上記の2つの構成方法を等しいと置くと，$$\tilde{b}:\tilde{a}=2 \odot \tilde{a}$$となり
これは，点群$$2m$$に同型な，拡張された点群であることがわかります．

（注）$$\odot $$
２つの直交する映進面$$\tilde{a}$$と$$\tilde{b}$$の組み合わせは，
交差する直線（不動線）がありますが，2回軸$$2$$と映進面$$\tilde{a}$$の組み合わせは，
互いに平行で交差しません．
記号$$ \odot $$は交差しない対称操作の組み合わせであるときに用いる記号です．
(注）拡張された点群 
$$\tilde{b}:\tilde{a}$$の組み合わせも，$$2 \odot \tilde{a}$$の組み合わせも，それらの対称操作を繰り返すと
並進の成分が生まれます．そのため，格子分だけ移動したものは同値としないと点群になりません．このような拡張された点群は，格子を核として写像すると点群に帰着できます．この場合は群$$2m$$と同型になります．

イスラムデザインの美しい壁紙をご覧ください．

pinterestからお借りたこのデザインは，Aziza（カタールのドーハを拠点とするアーティスト）によるものです．彼女は神聖幾何学とイスラムのパターンを研究しています．https://artofislamicpattern.com/#/6

この模様はとても魅力的で，イスラム模様の特徴がよく出ています．
色のグラデーションがとても素敵なのですが，ここでは幾何学の話をするので，色の区別ができない眼鏡をかけたと思って色は無視します．

この壁紙の成り立ちを，表紙の図に示しました．この図の平面群（全部で17種類あります）は，$$p4mm$$と記号で書かれるものです．このような繰り返しパターンは，モチーフ（非対称要素）となる図形を，$$p4mm$$の対称操作で配置し構成されます．

壁紙模様で，まず目につくのは周期（格子）で，これを平面群の記述の先頭に書きます．この例では，記号で$$p$$と書きました．2次元のブラベ格子のタイプは$$p$$（plain＝単純）と$$c$$（c-centred＝ｃ面心）の2つしかありません．そして，17種類の壁紙の対称性のうちの15種類が単純格子に分類されます．2次元の格子のタイプ分類（2次元のブラベ格子は5種類）は，前回の「ネットワーク・パターンの分類」で始めたところです（参照ください）．

この壁紙模様の例では，すぐ，黒い正方格子が目につきます．しかも，正方形の中心にも格子点のある（$$c$$面心格子）複合格子のように見えます．しかし，対角線の方向に目を配ると，一辺の長さが$$1/\sqrt{2}$$　になった，赤い正方格子（$$p$$格子）が見えてきます．

始めに気づいたc面心格子（黒い格子）は「正方形」の対称性ですし，後で気づいた$$p$$格子（赤い格子）も「正方形」の対称性です．$$c$$面心格子を作れたように見えましたが，黒い格子を$$1/\sqrt{2}$$に縮小し45°回転すると赤い格子と同じものになります．正方格子のは$$p$$格子だけで，$$c$$面心格子は存在しないことがわかります．

 この繰り返し模様のモチーフ（最小の非対称要素）は，赤い格子の1/8（黒い格子の1/16）の直角２等辺３角形です．このような3角形の模様付きタイルを作れば，そのタイル８つで赤い格子$$p$$格子の単位胞内を作ることができます．出来上がった単位胞を並べれば，無限に繰り返す壁紙模様が出来上がります．このモチーフは非対称要素と呼ばれるように対称性のない最小タイルです．

最後に，平面群の対称性の記法で，格子タイプ$$p$$に続く$$4mm$$は，格子点の対称性を記述する点群の記号です．
（注）平面群と点群の関係を正確に言うと：平面群は，格子を法とする準同型写像で点群に帰着します．

繰り返し模様の対称性の第５類は，
国際記号で$$pmg2$$，ロシア式記号で$$(b:a):m:\tilde{a}$$ 
（$$a$$の上に~を載せた記号$$\tilde{a}$$を,Texがつかえない場所では~$$a$$のように書くことにします）

 垂直な帯$$(b)･m$$を，水平方向のa軸に沿った映進面$$\tilde{a}$$で繰り返すことで得られる．
対称性の記号は$$(b:a):\tilde{a}:m$$と記述できる．上図に示したのはこの対称性のパターンの例です．このパターンの中で，つながっている２つのコイル状の曲線に注目しよう．一つは，s字の形になり，他方は逆s字の形になっている．2回回転軸は紙面に垂直で，S字曲線の中心とコイルの中心を通っています．尖った葉を束ねて尖った葉の先端が上を向いたり下を向いたりしています．
帯の対称性$$(b)･m$$は，$$(b):2$$　とも書けるし，映進面$$\tilde{a}$$は2回軸を面内に含むので，この2次元のパターンの対称性は，$$(b:a):m:\tilde{a}=(b:a):2･\tilde{a}$$　と記述できます．

束ねた葉の尖った先端を上に向けたり下に向けたりしているパターンは，蓮の花の円錐形のデザインでエジプトの伝統模様に見られます．

以下の模様も同じ対称性です．

（注）拡張された点群$$2･\tilde{a}$$は，格子分並進したものは同値と見なすことにすれば，点群$$2･m$$に同型です．映進面$$\tilde{a}$$の中に2回軸が含まれるので，記号$$ ⊙ $$を用いる必要はありません．

今回は第6類の対称性です．格子のタイプが$$p$$（単純格子）ではなく，面心格子$$c$$が現れました．国際記号で$$cm$$，ロシア式記号で$$(a/a)/m$$です．

ハート（対称性$$m$$）のモチーフが水平方向に$$a$$で繰り返され，垂直方向に$$b$$で繰り返されています．しかし，長方形（横$$a$$，縦$$b$$）の頂点にハートを配置しただけでは足りません．長方形の中心にも配置します．これは面心格子ですが，$$c=(a+b)/2$$の新しい周期ができています．このcを加えて$$(c/b:a):m=(a/a)/m$$と書かれます．古代のマウレタニアのパターンとのことです(Owen Jones)．

以下の中国のパターンも同じ対称性です(Owen Jones)．

等価なパーツで平面を隙間なく充填するこの対称性をもつパターン

 以下の例（pixtaのサイトからお借りしました）は，このような対称性です．

日本の伝統模様の青海波などはこの対称性です．以下参照

美しい幾何学p.88より

第７類の壁紙模様の対称性は，国際記号で$$pm$$，ロシア式記号で$$(b:a):m$$です．この対称性の模様は分かりやすく非常に単純なものになります．

表紙の画像（pngtreeの無料画像サイトからお借りたイスラム模様）は，この対称性に分類できます．以下の画像は，ちょっと見るとこの対称性のようですが，反S字のコイルになっているので鏡映面$$m$$はありません．

以下の模様も，$$(b:a):m$$の対称性の例です．日本の伝統模様のサイトからお借りしました．釘抜繋ぎという模様らしい．

]

一般的な，パターンは，上の図のようです．
長方形の単位胞の半分が非対称領域のタイルになります．

17種類の壁紙模様の対称性の第８類は，
国際記号で$$cmm2$$，ロシア式記号で$$(a/a):2･m$$　です．

点群$$2･m$$の図形を，並進の大きさは等しいが対称面(赤線)には斜交する軸（青線）$$(a/a)$$に沿って並進させて得られるので，$$(a/a):2･m$$と記述できる．
あるいは，面心格子$$c$$［黒いダイヤに注目すると面心格子が見えてきます］で，同じ点群$$2･m$$の図形を並進させると得られる．
菱形格子［単純格子］$$(a/a)$$の単位胞の面積は，面心格子［2格子点を含むものが単位胞］$$(c/b:a)$$の単位胞の面積の1/2です．

$$(c/b:a):2･m$$
$$(c/b:a)$$が面心格子を表し，$$m$$は赤い鏡映面を表し，鏡映面の交点には紙面に垂直に2回軸がある．

$$(a/a):2･m$$
菱形格子（単純格子）$$(a/a)$$を採用すると，このように記述できる．
これら両者の記号は同じ対称性を表現している．$$(c/b:a):2･m＝(a/a):2･m$$

このような対称性で，等価なパーツだけで平面を隙間なく（重なることもなく）充填するパターンは次のようなものです．釣鐘の形が非対称要素（モチーフ・タイル）で菱形の単位胞（単純格子）は２つの釣鐘型からなり，面心格子の単位胞は，４つの釣鐘型からなります．

次の例は，この対称性の日本の伝統文様「菱文（ひしもん）」です．この図はネットからお借りしました．

■平面群の記号，$$(c/b:a):2･m$$や$$(a/a):2･m$$の記述に使うのは，群を定義する最小の対称要素［群の生成元］だけ記載します．下図を見てください．完成した平面群の対称要素のなかには，生成元だけでなく，細い赤い線［映進面］や白抜きの赤い2回軸が生じています．

菱形格子と，面心格子のそれぞれの単位胞を下図に着色して置きました．

今回は壁紙模様の第９類で，国際記号で$$pmm2$$，ロシア式記号で$$(b:a):2･m$$です．

対称性$$2･m$$の単位胞図形を長方形の格子$$a$$軸，$$b$$軸で並進してパターンができます．
以下の図は，この対称性のパターンとはわずかに違うのですが，どこが違うかわかりますか？
間違い個所を見つけてください．

 例えば，ダイアモンドを頂点とする長方形が単位胞ですが，この単位胞の中身の対称性は，どうでしょうか．中心に2回回転軸はありますか？確かに，垂直に鏡映面はあります．よく見ると，コイルの巻き方は鏡映対称を満たしていますが，2回回転対称とは矛盾します．従って，厳密に言うと単位胞の対称性は$$2:m$$でなく$$m$$ですので，パターンの対称性は，$$(b:a):m$$，国際記号では$$pm$$の繰り返し模様になっています．
それでは，厳密にこの対称性$$(b:a):2･m$$である別の例を探してお知らせください．日本やイスラムの伝統模様で見つかると良いのですが．不思議なことになかなか見つかりません．自分で作った方が速いかもしれません．

もし，先に掲載した例を修正するなら，渦巻きコイルでなく同心円に変更します．蔓の重なり方も紙面上下の立体感を失くして平面内にある様に変更します．表紙の図のようになります．ただし，蔦の重なり方を修正していないので，2回対称を満たしますが，鏡映対称に矛盾します．両者を満たすには，蔦の重なりが，平面上にある様に修正する必要があります．しかし，あまり面白いデザインではないので，もっと良いデザインに皆様ご挑戦ください．

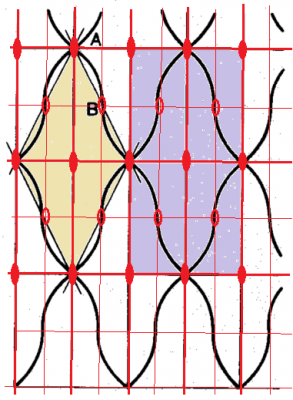
繰り返し模様の対称性の第10類は，国際記号で$$p4$$，ロシア式記号で$$(a:a):4$$．単位胞の図形の対称性$$4$$を，直交する軸（従って，正方形のメッシュが格子）に沿って並進して得られるパターンで，$$(a:a):4$$で記述される．以下の２つのエジプト模様の例は，ちょっと見るとこの対称性のようですが，厳密には，この対称性を満たしません．

問　どこがいけないのか間違い探しをしましょう．

 解答

左のパターンでは，背景にストライプがありますので，4回対称軸は2回対称軸に低下します．そして，格子は直交している必要がなくなり，対称性は$$(a:a):2=(b/a):2$$になります．
右のパターンでは，コイルの渦巻きは2回回転対称のようですし，花は花弁が10枚のようですから，単位胞の中身は全体として4回回転対称になりません．

等価なパーツが隙間なく平面を充填するパターンの例
この対称性のパターンは，正方形の格子並進，4回軸がありますが，鏡映面はありません．モチーフ（非対称要素）は単位胞の1/4(例えば薄桃色)です．パターン全体を見ると，それぞれのパターンには対掌体（風車の回り方が逆なもの：chiral，enantiomorphs）が存在します．

この対称性のエッシャー作品の例を以下に示します． 

美しい幾何学p.99より

対称性の第11類です．国際記号$$p4gm$$，ロシア式記号$$(a:a):4･\tilde{a}$$

このパターンは，4回対称の単位胞を，２つの等価な互いに直交する映進面で繰り返し広げて得られる．
縦，横の映進面$$\tilde{a}$$は，群$$4･m$$に同型な，法による点群$$4･\tilde{a}$$の4回軸を通る．

 上の図はこの対称性のエジプトのパターンと言いたいが，厳密に見ると4回軸はなく２回軸になっている．
（間違い探し：４回対称性を破っているところを探しなさい）

 縦，横の太い赤線は鏡映面．細い赤線は映進面．映進面の交点に4回回転軸がある．太い線の交点には2回回転軸が生じている．

単位胞の面積は，非対称要素（モチーフ）が8個で出来ている面積に等しい．

以下の図は，pngtreeのサイトから借用したもので，今回の対称性の図の例です．

繰り返し模様の対称性の第12類は，$$4･m$$の図形を正方形単純格子$$(a:a)$$で並進させて得られる．

この対称性は，国際記号で$$p4mm$$，ロシア式記号で$$(a:a):4･m$$と記述される．
この対称性のパターンの例は

非対称要素（モチーフ・タイル）は，単位胞の1/8です．

この対称性の日本の伝統模様はたくさんあります．
例えば，以下の七宝つなぎなどです．イスラムの模様との交流もあったと思われます．

\begin{array}{|c|c|c|c|c|c|c|c|c|c|}
\hline
\textgt{国際記号} & p1 & p2 & pm & pg & cm & pmm2 & pmg2 & pgg2 & cmm2 \\[0mm]
\hline
\textgt{ロシア式記号} & \left( b/a \right) 1 & \left( b/a \right) :2 & \left( b:a \right) :m & \left( b:a \right) \tilde{b} & \left( a/a \right) /m & \left( b:a \right) :2m & \left( b:a \right) :m:\tilde{a} & \left( b:a \right) :\tilde{b}:\tilde{a} & \left( a/a \right) :2m \\[0mm]
\hline
& & & & & \left( c/b:a \right) :m & & \left( b:a \right) :2\tilde{a} & \left( b:a \right) :2 \odot \tilde{a} & \left( c/b:a \right) :2m \\[0mm]
\hline
\textgt{対称要素} & \begin{minipage}[b][95pt]{130pt}
\includegraphics[width=130pt,height=95pt]{tex17tplaneable_001.bmp}
\end{minipage}
& \begin{minipage}[b][86pt]{121pt}
\includegraphics[width=121pt,height=86pt]{tex17tplaneable_002.bmp}
\end{minipage}
& \begin{minipage}[b][85pt]{93pt}
\includegraphics[width=93pt,height=85pt]{tex17tplaneable_003.bmp}
\end{minipage}
& \begin{minipage}[b][86pt]{97pt}
\includegraphics[width=97pt,height=86pt]{tex17tplaneable_004.bmp}
\end{minipage}
& \begin{minipage}[b][80pt]{97pt}
\includegraphics[width=97pt,height=80pt]{tex17tplaneable_005.bmp}
\end{minipage}
& \begin{minipage}[b][88pt]{103pt}
\includegraphics[width=103pt,height=88pt]{tex17tplaneable_006.bmp}
\end{minipage}
& \begin{minipage}[b][112pt]{141pt}
\includegraphics[width=141pt,height=112pt]{tex17tplaneable_007.bmp}
\end{minipage}
& \begin{minipage}[b][113pt]{132pt}
\includegraphics[width=132pt,height=113pt]{tex17tplaneable_008.bmp}
\end{minipage}
& \begin{minipage}[b][113pt]{131pt}
\includegraphics[width=131pt,height=113pt]{tex17tplaneable_009.bmp}
\end{minipage}
\\[0mm]
\hline
\end{array}
\ \\
\ \\
\begin{array}{|c|c|c|c|c|c|c|c|c|}
\hline
\textgt{国際記号} & p4 & p4mm & p4gm & p3 & p3m1 & p31m & p6 & p6mm \\[0mm]
\hline
\textgt{ロシア式記号} & \left( a:a \right) :4 & \left( a:a \right) :4m & \left( a:a \right) :4 \odot \tilde{a} & \left( a/a \right) :3 & \left( a/a \right) :m & \left( a/a \right) m & \left( a/a \right) :6 & \left( a/a \right) :m \\[0mm]
\hline
& & & & & & & & \\[0mm]
\hline
\textgt{対称要素} & \begin{minipage}[b][116pt]{121pt}
\includegraphics[width=121pt,height=116pt]{tex17tplaneable_010.bmp}
\end{minipage}
& \begin{minipage}[b][116pt]{115pt}
\includegraphics[width=115pt,height=116pt]{tex17tplaneable_011.bmp}
\end{minipage}
& \begin{minipage}[b][114pt]{119pt}
\includegraphics[width=119pt,height=114pt]{tex17tplaneable_012.bmp}
\end{minipage}
& \begin{minipage}[b][109pt]{147pt}
\includegraphics[width=147pt,height=109pt]{tex17tplaneable_013.bmp}
\end{minipage}
& \begin{minipage}[b][98pt]{145pt}
\includegraphics[width=145pt,height=98pt]{tex17tplaneable_014.bmp}
\end{minipage}
& \begin{minipage}[b][99pt]{143pt}
\includegraphics[width=143pt,height=99pt]{tex17tplaneable_015.bmp}
\end{minipage}
& \begin{minipage}[b][98pt]{145pt}
\includegraphics[width=145pt,height=98pt]{tex17tplaneable_016.bmp}
\end{minipage}
& \begin{minipage}[b][98pt]{147pt}
\includegraphics[width=147pt,height=98pt]{tex17tplaneable_017.bmp}
\end{minipage}
\\[0mm]
\hline
\end{array}

壁紙模様の対称性の第13番目の類は，対称性3の図形を，60°で交差する２つの等価な並進軸$$(a/a)$$で並進して得られる．

国際記号で$$p3$$，ロシア式記号で$$(a/a):3$$です．今回から始まる残り５つの対称性の類（第13~17）は，正3角形のメッシュに属します．

等価な図形が隙間なく平面を充填しているこの対称性のパターンを以下に示します．モチーフ（非対称要素）は，正3角形メッシュ座標を作っている頂点に集まる曲線で囲まれた形です．

非対称要素（モチーフ）３つで，単位胞の面積に等しくなります．鏡映対称はありません．

以下の例は，アルハンブラの有名なモザイクです．これは対称性$$p3$$の例です．ただし，色の区別はしていません．

（参考）以下の「千鳥」のパターンの対称性は$$p3$$ではありません．何故でしょうか？

（解答）上図の「ちどり」のパターンは，単位胞の菱形の頂点に6回軸がありますので，$$p3$$ではありません．このパターンは，後ででてくる$$p6$$の対称性です．単位胞の中を，2つの千鳥図形で埋まますが，この千鳥の形は，等価なモチーフにさらに3分割できますから，非対称要素は，千鳥を3分割したものになります．

■第14の類は，国際記号で$$p3m1$$，ロシア式記号で$$(a/a)：m･3$$と記述します．対称性$$3･m$$の図形を60°で交差する等価な２つの軸$$(a/a)$$に沿って並進させて得られますが，鏡映面（赤色）の入り方が，並進軸（青色）に直交している．

非対称要素（黄色）が6個で単位胞を埋める．

■第15の類は，国際記号で$$p31m$$，ロシア式記号で$$(a/a)･m･3$$と記述します．並進の格子$$(a/a)$$は同じですが，鏡映面の入り方が，並進軸方向に平行である．

上の図で鏡映面は格子に重なっている．非対称要素（黄色）が６つで単位胞を埋めている．

■この両者の区別は多くの書物で混乱がみられます．分かりにくいので，もう少し詳しく説明を加えましょう：

美しい幾何学，p.100，p.110より引用

■第16の類は国際記号で$$p6$$，ロシア式記号で$$(a/a):6$$です．

以下のペルシャのパターン（Owen Jones）の例では，黒い6角形の内の花は厳密には6回対称ではありませんが，これを6回対称とみなすと，周りに風車がまわっているような6回軸の配列のパターンが見えます．

6回回転軸が通る点を頂点とする平行4辺形が単位胞．非対称要素モチーフが6個で単位胞を埋めます．

 エッシャー作品の例

■第17の類は国際記号で$$p6mm$$，ロシア式記号で$$(a/a)･m･6$$，あるいは$$(a･a):m･6$$です．

$$p6$$の対称性に鏡映面が加わりますが，並進軸に平行な鏡映面も，垂直な鏡映面もあります．

非対称要素である直角3角形が12個で単位胞を埋めます．

 対称性の法則をもっと利用すると，アーティストがデザインパターンのモチーフを変形するのが容易になる．

17種類の平面群の対称要素のマップとパターンを一覧にまとめます．

■17種類の平面群の対称要素のマップ

■17種類の平面群の非対称モチーフのパターン

人間は様々な用途で無限に繰り返す平面パターンを使います：壁紙，寄せ木細工，タイルの床，瓦屋根，陶器や装飾石の壁，レンガや敷石，道路や広場の舗装，色織物，カーペットや編物，同一物の密な充填，金属やプラスチック板から標準物を大量に打ち抜く，その他の多くの分野で利用されます．

自然界の網目パターンは，魚の鱗，生体組織の細胞，ハチの巣，マツカサの鱗片，などの配列で見られます．特に興味深いのは，結晶中の，原子・イオン・分子が配列した網平面です．もちろん，これらを直接見ることはできませんが，X線や電子線の回折や，走査型顕微鏡を用いて観測できます．
網目パターンから受ける印象を分析すると，芸術家が特定の視覚効果を伝えるために，特定の対称性クラスを意識的に選択する法則を確立できるかも知れません．

例えば，斜交する並進軸を持ち，対称面を持たないパターン（図112）は，斜め方向の動きを強調したい場合に適しています．

階段，ロビー，エスカレーター，地下鉄の傾斜トンネル，アーチ橋のフェンスなどの壁を飾る際に，芸術家はこの問題に遭遇します．

図117　　　　　　　　　　　　　　　　　　図121　　　　　　　　　　　　　　　　　　図123

水方向の並進軸はあるが，垂直方向の対称面を持たないパターン（図115，117参照）は，特定方向として水平面に沿った動きを強調しているので，地下鉄や回廊の水平通路の装飾に用いると成功します．対称面があると，それらに垂直な方向への運動を止めます．例えば，図121,123などのパターンは，水平方向には静止しているように見えます．図121では，２回軸が存在することで，上下方向への運動の概念が生まれますが，図123では，それらの回転軸が存在しないので，上方向，あるいは一般的に，垂直な一方向の運動の印象を与えています．
図121は，回廊の水平な床や天井の装飾にふさわしく，図123は， 地下鉄の昇降路の床や天井の装飾に適しています．

　図128　　　　　　　　　　　図130　　　　　　　　　　　図137　　　　　　　　　　　図147

水平や垂直の対称面のシステム（図128,130,137,147）がいくつか存在することで，静止休息，記念碑性，不動性，重力などの印象を醸し出します．興味深いことですが，(b:a):2･m型の対称パターン（図128 と 130）は，長い間，壁紙に使用されてきました．そして，図137や147に示すようなさらに対称的なパターンは，寄せ木，天井，ステンドグラス窓などには使われました．
奇妙な静止のない印象は，主要部分に映進面がある対称パターン（図116と120）で生み出されます．言葉でうまく表現できないのですが，これらのパターンの中の図形が，押し合い，転がり，絡み合い，群がって動きがあります．

　　　　　　　　　　　図116　　　　　　　　　　　　　　　　　　　　図120

このタイプの対称性は，他の対称性よりも出会う頻度は少ないのですが，それは，他のものよりも構成や認識が困難であるためで，例えば，見本市会場や遊歩道などのデザインに利用されることがあります．

　　　図132　　　　　　　　　　　　図139　　　　　　　　　　　　　　図145

特に興味を惹くのは，対称面がなく，3,4,6回回転対称軸で特徴づけられるパターン（図132,139,145）です．このようなパターンは，そのダイナミックさから，ダンスホールなどの大勢の人が無秩序に動くことを想定した施設の床や天井に適しています．図116のようなパターンと合わせて，文化公園の広場やサーカスのテントのアリーナ，フローティング・パネルなどの装飾に使用されています．全体として静止休息の奇妙な印象と細部に見られる動きは，普通の対称面と映進面が交互に繰り返すパターンのせいで生じています（図12,135,142）．静止休息と運動の印象のどちらが支配的になるかは，フレーム・ワーク（垂直，水平線に）に対するパターンの方位に大きく依存します．

　　　図135　　　　　　　　　　　　図142

例えば，図12はこの本に掲載している向きでは，動きの印象が静止に打ち勝ってしまう．特別な注意を払わずにパターンを見ると，対称面を見落とすのです．
一方，図12と同じ対称性を持つ図135は，動きよりも静止の印象が打ち勝ってしまう．それは，本を普通に置いたときに，パターンの対称面は垂直・水平線に沿ったフレームに平行であるからです．
観客が網目パターンを見たとき生じる印象に対称性が演じる役割について詳しく述べてきました．明らかに，対称性が美的鑑賞の唯一の要因ではありませんが，パターン構築の基礎となる法則を明らかにすると，装飾美術で対称性の果たす役割は，デッサンで遠近法が果たす役割と同じです．

■最後に，私が気に入っている映進面のある軽快な歩道タイル張りの写真を掲載します．美しい幾何学（技術評論社）p.93より

技術的な応用●ブラッグの法則 ●干渉

10cm×10cm程度の薄い布（ナイロン，カプロン，絹）を2枚重ねて，繊維が小さな角度（5°-10°）で交差するようにする．これを2枚のガラス板の間に挟み透過光で全体を観察すると，モアレパターンと呼ばれる自然界で広く見られる現象（科学技術で頻繁に利用される）が観察できる（図151）．モアレパターンの対称性乱れは，干渉を起こすネットの不完全性に起因するものである．もし，これらが完全に規則的なネットならば，不規則なモアレではなく規則的な二次パターンが現れる．この現象は，写真印刷などで，ガラス板の上に細かい黒格子が描かれたスクリーンを通して写真を撮影するハーフトーン印刷で見られる．

Fig.151

しかし，「スクリーン効果」は必ずしも作品の邪魔をするものではなく，布地や壁紙などで優れたパターンを作るために使われることもある．
■2 つの無限平面パターンを重ね合わせたときに，どのようにして二次的なパターンが発生するのかを理解するために，最も単純な例として2 つの同一な平行縞を重ね合わせた場合の例を見よう．図152に示すように，２つの１次元縞の相互作用（干渉）の結果，一次の縞（元の縞）の繰り返し周期よりも大きな繰り返し周期の二次的な幅広の縞が生成される．実際には，これらの二次的な幅広縞は，一次の縞によって形成されたジグザグに過ぎない．一次の縞の間隔を，目で解像できない程度（0.1mm以下）まで小さくすることで，二次的な縞だけが見える画像が得られるが，これは一次の縞の一つを拡大したものになる．
一次縞周期（一本の縞の幅＋縞間の間隔）を$$λ$$，二次縞周期 を$$d$$，一次縞系が交差する角度$$2θ$$ とすると，簡単な計算で，$$λ=2dsinθ$$　が得られる．
すなわち，一次縞周期は，二次縞周期の２倍に一次縞間の交差角度の半分の$$sin$$を乗じた値に等しい．

Fig.152

結果として得られる式は，よく知られているブラッグの法則と全く同じになる．ブラッグの法則中の量λはX線の波長であり，$$d$$はX線を反射する結晶の原子網面の間隔，$$θ$$は入射X線と反射面の間の角度である．
このアナロジーで，結晶構造の幾何学のX線による研究を，モアレ現象に還元することができる． [例えば,Bollmannの本(1970)を参照]

■今度は，平行縞の2つの系を2つの同一正方形の網にしよう．交差角2θが十分小さな角度なら，2次的に生じる像は，最初の網を単純に拡大した，少しぼやけた像になる（図153）．

図153

一次の系の網目４角形の辺は，以下のように計算できます．
一次ネットと回転した一次ネットを重ねて生じる二次のネット網目の寸法に関しては，既に述べた1次元での関係がやはり成立します．

上記の２つのケースの図柄の重ね合わせで，角度$$±2θ$$の小さな角度で重ね合わせても，$$180°±2θ$$で重ね合わせても違いがなかったのは，図柄に2回回転対称性があるためである．
2回回転対称のない図形，例えば，3角形の系（図154）を重ね合わせるとすると，この二つの回転角度の効果にはかなりの差がでる．

小さな回転角$$2θ$$では，二次的な絵柄（図155）は楕円の系のようなものであるのに対し，回転角$$180±2θ$$では，二次的な絵柄（図156）は三角形で構成されて，一次的（元の）な絵柄の拡大と考えてもよい．

図154

図155

図156

図157

図158

詳細に検討してみると，角度$$2θ$$が十分に小さく，一次パターンが周期的に繰り返される小さな素図形をかなりの数持っている場合には，$$180°±2θ$$の角度で2つの同一のパターンを重ね合わせると，無限の対称平面パターンが拡大された形で得られることがわかる．
実際には，これらの条件を満たすことは非常に困難なことが多いので，この実験は最も単純な種類の素図形でしか合理的な成功はしません（図157と158）．

２つの同一な網目パターンを種々の回転角度で重ねたときの干渉で，何が起こるか考察しよう．例として，面心の長方形（面心斜方格子）の頂点に円環を配した網目パターンの系（図110d）をとり上げる．

Fig.159

Fig.160
図159と160を見ると，角度2θが小さいうちは，二次的図形は（素図形の数が不十分なために）一次図形の拡大図となることがわかる．角度２θが大きくなるにつれて，拡大の度合いは小さくなる．面心斜方ネットの対称性を保ったまま，パターンは非常に大きく形を変え始める．図示された一連のパターンは，例えば壁紙や織物に適したパターンの豊富な品揃えが，互いに相対的に異なる角度にある２つの同一の周期構造の単純な機械的重ね合わせによって得られる可能性があることを示している．この可能性を考えると，一連の疑問が湧く．例えば，同一の周期構造の負あるいは正の重畳によってどんな効果が得られるだろうか．実験を上記に記述したパターンで行うと，二次的に生じた6角形の各中心に暗い丸点が形成されることが判明した（図161）．

図161

特に興味深いのは，異なる図形を重畳したときの，対称性の相互作用に関する問題である．一般的な重畳と同一対称類の等価系の重畳，右手と左手系パターンあるいは異なる色に塗られた図形の相互作用などである（図162）．
これらの疑問は，ほとんど研究されたことがないが，我々は複合系の対称性原理を使い，これらを調査してみよう．この原理は12章で紹介する．

無限のパターンの重畳の結果として得られる二次的形の多様性にもかかわらず，等式$$λ＝2dsinθ$$は変わらずに残る．そこでは，同じネットが2つの
のパターンが選択され，かつ，角度$$2θ$$があまり大きくない場合には

図163（正の左手系パターンを負の右手系パターンの上に重畳）では，第二次パターンが一時のパターンの基底である正方格子を再現しているのがはっきりわかる．後者は黒が正，白が負の小さい3角形の行からなる．

網目の拡大率（すなわち$$d/λ$$の比）と角度$$2θ$$は互いに密接に相関している図から決定され，この式が問題のケースに適用可能であることを示している．

結論として，周期の異なる2つの縞模様の平行重ね合わせを考えてみよう（図164）．
このケースは，音響学，光学，無線技術，その他の波動物理の分野で出会うビート現象幾何学的な描像を提供するので興味深い．
この現象は，同じ方向に移動する波長がわずかに異なる２つの平面波があるとき，二次的に長い波長の波が生じる現象で，音響学的には周期的な音の強弱（ビート）として観測される．
ビートは近似的に調整された2つの音叉を同時に鳴らすことで簡単に作れる．
実際には，2つの同じピッチの音叉の一方だけに，ワックスを貼り付けてチューニングをずらす．

平行な2つのシステムの重畳で生じるビートは，図164に示すように，第1のシステムの2本の連続した縞の間の距離は，$$λ_{1} = 1.91$$ mm；第2のシステムでは，この距離は$$λ_{2}＝1.60$$mmである．

これらの2つの量は、一次干渉の波長と呼ばれることがある．
距離$$Ｌ＝9.86$$mmは，密な隣接距離で，二次的な波長あるいはビート波の波長と同じである．

これらの量の関係をより詳細に検討すると次の式が得られ，既知の$$λ_{1}$$，$$λ_{2}$$から，二次波の波長Lを計算することができる：$$L=\displaystyle \frac{\lambda _{1}\lambda _{2 } }{\lambda _{1}-\lambda _{2 } }$$

今日はモアレの実験を行います．

まず，網目パターンを用意します．今回は，面心斜方格子［長方形格子の中心にも格子点のある複格子（2格子点胞）］を使います．この格子は，単純格子（1格子点胞）で解釈すれば，菱形格子に還元できます．この関係は下図を見るとわかるでしょう．

上図では，格子点に正3角形を配しました．配置した正3角形の対称要素と格子の対称要素を比較すると，共通な対称要素としては垂直方向の鏡映面しかありません．従って，パターン全体としての対称性は，垂直方向の鏡映対称を持つだけです．格子自体にあった高い対称性も，正3角形自体にあった高い対称性も互いに打ち消し合って残りませんでした．これを対称性の重ね合わせ原理と言います．

このようなパターンを基礎にして作った網目模様を以下に示します．

この網目網を互いに2θ（小さい角度）で重畳したときに，生じる2次的網目パターン（モアレと呼ぶ）を調べましょう．

　　　　　(1)重畳角2θ（小）のとき　　　　　　　　(2)重畳角2θ（大）のとき

　　　　　　(3)重畳角180のとき　　　　　　　　　(4)重畳角180°+2θ（小）のとき

 
（５）

 結論：いずれの場合も2次的なモアレ像に生じる格子のタイプは，初めの（1次の）格子のタイプと同じであることがわかる．しかし，2次的に生じるモアレ像中に正3角形の対称性がどのように反映されるかの鮮明な結果は得られなかった．

ネットワークパターンをカットするためには、矩形，正方形，正3角形，正6角形の紙シートを使います．
初めの紙の形が矩形なら，紙のサイドに沿って半分に折るを繰り返し，折り畳んだ状態で切り込みを入れます．すると，対称面と2回対称軸のあるパターンが得られます（図 165）．［訳者注）この図形の対称性は2mmです．mは図形全域に有効な対称面ですが，この図形には局所的に有効な対称面があります．対称面は紙の折線に沿って生じるのですが，全域的な対称面と局所的な対称面を区別したいものです．］

正方形の紙から始めて，サイドの線に沿ってだけではなく対角線に沿ってもこれを半分に折ることを繰り返すと，対称面と4回対称軸のあるパターンを切り出すことができます（図166）．

最初に正３角形の紙から始めて，３角形の２等分線に沿って折ると，対称面と3回対称性のあるパターンを切り出せます．
正６角形から始めても同じ結果が得られます．正６角形の内部に正6角形と共通の頂点を持つ正３角形を内接させ，３角形の２等分線に沿って，あるいは内接された３角形の辺に平行な線に沿って折ります（図167）．

正6角形のサイドに沿って2つ折りすると6回対称軸が得られます（図168）．

これらの切断例は，（ホロヘドロン）完面像図形＝そのネットワークパターンの対称性で許される最大の対称要素を与えます．
対称面のないパターンの切込み(あるいは一太刀切)は例外で，困難があります．このような場合には，重ねた紙からたくさんのロゼットをカットして，平面パターンや層の対称性の法則（次章を参照）に従って，異なる色の背景のボード上に，それらを貼り付けて作ります．
後者の場合は，紙の表裏にも注意を払わなければなりません．
図169に，このように切断した平面パターンの例を掲載しています．

［訳者解説］折線は対称面になります．対称面を赤線で示しました．どのように折って切ったか推定してください．

ここで対称面と言っているものには局所的に通用するもの（青色）と，全域的に通用するもの（赤色）とがあります．これらは区別しましょう．

正則点系
点の多重度とその相対数の積の保存則

［訳者注）単位胞中に存在する原子の数によっては，対称性（多重度）によりその原子の存在できる場所が決まっつているという便利な性質が，構造解析のときに利用できる］

有限図形の点系（同価な点の系）に関して，対称（正則）の概念には，すでに出会っています．この概念を無限の平面図形に拡張するのは困難ではありません．何らかの無限の平面図形（下図173）が与えられたとしましょう．その中の任意の1点（図173の任意の●）を選び，選んだ点に同価なすべての点を見出しましょう．
［訳者注）同価な点というのは，対称操作で互いに変換できる点のことで，図173の場合には，実線が鏡映面，および，各鏡映面に沿った並進が定義されています］

その結果得たすべての点の集合は，同価点の１つの単純正則点系を作ります．これに，2番目，3番目，等々の同価点系（○，◎）を加えると，複雑，あるいは，複合点系を得ます．もし，単純点系の初めの点が対称面上や対称軸上や，対称中心になければ，得られた集合は一般点の同価点系（●）と呼ばれ，他の場合は，特殊点の同価点系（○，◎）と呼ばれます．
［訳者注）●だけ集めると一般点の系，〇だけ集めたものは鏡映面上の特殊点の系，◎だけ集めると鏡映面の3重点（あるいは，3回軸）上の特殊点の系］

無限パターンの各タイプ点系の点の数は無限ですが，単位胞の中の点の数は有限です．（これらは対称演算により互いに移り合う）

図173を調べると，◎の点１つに〇の点3つ，●の点6が対応し存在することがわかります．これを，●の多重度は１，○の多重度は２，◎の多重度は６であるといいます．黒点●の位置を徐々に対称面方向に動かすと，それが対称面上を通過するとき，両側から近づいた2つの黒点●は1つに合体します．もし，黒点●が３回転軸の位置に近づき，ちょうど軸上（に3つの対称面の交差点）を通過するときには，6つの黒点が1つに合体します．
したがって，各単位胞の中にある，さまざまなタイプの点の相対数$$n_{i}$$は，対応する多重度$$s_{i}$$の逆数に比例することになります．

$$n_{1}:n_{2}:n_{3}: \cdot \cdot \cdot \cdot \cdot =\displaystyle \frac{1}{s_{1 } }:\displaystyle \frac{1}{s_{2 } }:\displaystyle \frac{1}{s_{3 } }: \cdot \cdot \cdot \cdot \cdot \cdot $$
$$n:n_{1}:n_{2}: \cdot \cdot \cdot \cdot \cdot =1:\displaystyle \frac{1}{s_{1 } }:\displaystyle \frac{1}{s_{2 } }: \cdot \cdot \cdot \cdot \cdot \cdot ,$$ あるいは，$$n=n_{i} \cdot s_{i}$$

どんなパターンにも多重度s=1の点が存在するので，そのような点の相対数をnと記すと2番目の式のように書き換えられます．

言い換えると，特定の種類の点の相対数とその多重度の積は一定です． したがって，図173のパターンの例では，点の多重度と相対数の積は常に6に等しくなります． 黒点●の場合は1x 6，白点〇の場合は2 x 3，二重円◎の場合は6 x1です．
規則的な点の系（正則点系）を記述するのに，平面パターン全体を作る必要はありません． 対称要素の集合をその特定の領域（たとえば単位胞の内）で指定するだけで十分です． 対称要素の配置図が与えられれば，特定の位置に点を配置し，その対称要素を作用させて，与えられた対称クラスに対応する同価点の系を簡単に構築できます．

［訳者注）下図の２つは，対称要素の配置図（上図）に対して，一般点に非対称図形楔型を置いて得た点系（下図）の例です］

平行多辺形とプラニゴン 

寄せ木細工での利用

一つの図形を用いて，平面を隙間も重なることもなく埋め尽くす課題にしばしば出会います．図形を互いに平行配置し平面を埋め尽すことができ，その図形がポリゴン［凸多角形］であれば，その図形は平行多辺形parallelogonと呼ばれます．任意の平行４辺形と，対辺が平行で等しい6辺形だけが，平行多辺形になれ，この他に平行多辺形はありません．こうして，次の８つの典型的な平行多辺形が作れます（図171）．内訳は，4つの平行多辺形（正方形，長方形，菱形，傾いた平行4辺形）と，４つの平行6辺形（正6角形，対辺に垂直な方向に伸びた６辺形，対角を2等分する方向に伸びた６辺形，歪んだ6辺形）です．

平行多辺形からプラニゴンplanigon（すなわち，平面を隙間なく重ることもなく埋め尽くす形の平行多辺形で，平行移動だけでなく回転軸や対称面で反射した位置にも配列できる）を得るには，各平行多辺形を対称性に従い等価な部分に分割すれば十分です．例えば，正方形は８通りの方法で等価な部分に分割できます（図172，19-26）．もし，正方形を非対称図形として扱えば，分割できず(19)のままであり，この場合は平行多辺形であると同時にプラニゴンでもあります．もし，正方形を対称性2･mにするなら，等価な部分への分割には２つの方法があります（20,21）．2回回転対称性を持たせるなら２つの台形への分割になります（22）．対称性4･mにする，正方形の4つの等価部分への分割なら2通り（23,25），および，８つの等価部分への1通りの分割(26)があり，4回回転対称性にするなら，４つの等価部分への分割は１通り(24)があります．すべての平行多辺形の等価部分への分割は，これと完全に同様な方法で行います．図172には全部で48通りの平行4辺形のプラニゴンへの分割結果が掲載されています．ただし，これらの分割された平行多辺形の48個のうちのいくつかは，平面を埋めるた結果が同じになります．例えば，平行多辺形19と23は，同じ単純正方格子になります．また，平行多辺形21,25,26は直角2等辺3角形の異なる寄せ木パターンを作ります．
平面をプラニゴンで埋める問題は，確かに，もっと一般的な問題の特殊なケースで，等価な図形で平面を埋める問題は早くから考察されてきました．この特殊なケースは，床や道を張り詰める寄せ木デザインなどで実用的な重要性があります．

[訳者注]ここで扱う平面の分割は，結晶（周期的内部構造）学の基礎になるもので周期的なものであります．ペンローズタイリングのような非周期の平面分割（充填）もあります．

万華鏡でネットワークパターン
 
［訳者注］ここでは万華鏡で作るネットワークパターンについて述べているが，平面のタイル張りの対称性（5つのブラベー格子）が念頭にある．万華鏡は鏡の組み合わせで作られる対称性なので，そのうちの4つのブラベ格子が実現しうる．これらは格子の対称性そのもの（その格子で許される最も高い対称性）で完面像と呼ばれる．

完面像クラスの４つのパターンだけが万華鏡で作ることができる．これらは紙の折り畳みとカットにより作れるパターンと同一である．長方形の辺に沿って鏡の表面が内部に向くようなプリズム配置からは，(b:a):2･m型のパターン（図170a）が生れる．元の物体はプリズムの内部に置かれる．直角2等辺3角形の周りに置かれた鏡配置により(a:a):4･m型のパターン（図170b）が生まれる．正3角形の辺に沿って配置された鏡の万華鏡は(a/a):m･3型のパターン（図170c）を生む．そして，鋭角が30°, 60°の直角3角形の辺に沿って3枚の鏡を配置した万華鏡は(a/a):m･6型のパターン（図170d）を生む．実際には，これらの万華鏡は，帯状の鏡を繋ぎ合わせて作る．プリズムの底を艶消しガラス，もしくは，外部あるいは内部に艶消しガラスの物体を置く．初めの２つの場合は，万華鏡を水平に持ち，光源に直接向ける．最後の場合は，垂直に持ち下から照明する．

［訳者注］ここで実現される万華鏡は，4枚鏡の長方形の他に，平面を隙間なく埋め尽くす３角形の3種類（以下の説明では整数解の3角形）に関するものだけで，分数解の3角形は考慮していないので，以下の説明を補足したい：

美しい幾何学，p109，p118より

2次元アイソゴンとアイソヘドラ．寄せ木

アイソゴンisogonとは，どの頂点にも同じ数の辺が集まっている多面体に与えられた名前です．各頂点に集まる辺の様子が合同であるか鏡映対称であるような典型的なアイソゴンに興味を絞ります．典型的なアイソゴンの例には，すべての正多面体が含まれます．一般的なアイソゴンのすべての頂点は球面に乗り，球の半径が無限に大きくなると，球の表面は平面になります．半径が無限大の球に対応する典型的なアイソゴンを，平面アイソゴンと呼びます．
一般に，平面アイソゴンは，隙間なく平面を埋めるいくつかのタイプの多角形（＝ポリゴン，平面アイソゴンの面）で構成されます．平面アイソゴンの各頂点は，幾何学的に等価（合同または鏡像）な様相でアイソゴンの辺（ポリゴンの側面）が集まっています．平面アイソゴンを構築してみましょう．ネットワークパターンの17の対称クラスのうちの1つを選び，図149を使用して，選択した対称クラスに対応する対称要素の配置を紙に書き留めます．次に， 任意の点を選び，その点に存在する対称要素の対称変換を作用させます．
結果として得られた同価点の系が，アイソゴンの構築の基礎になります．系の各点の最近接点を線分で結びます．検討中の点を除いて直線の交差が発生しない限り，このプロセスを続行します．等しい最短距離が複数ある場合，これらが交差しない限り，対応するすべてを線分で結びますが，交差する直線は描画しません．図174〜176の番号1〜35は，種々の対称クラスに対してこのようにして構築された平面アイソゴンです．
例として，アイソゴン2（図174）がどのように構築されたかを考えてみましょう．同価点の単純系を構築するには，対称クラス(a / a):m･6（図149）を選びます．6回対称軸と3回対称軸の間の対称面上に点Aを選定します［訳者注）Aは特殊点です］．この系の点Aの同価点のすべてが，3回軸と6回軸の回転により生じます．点Aを隣接する2つの点と結びます．同様の作業を系のすべての点で行います．このようにして，図に示されているすべての６角形を完成します．
次に，点Aと同価点のうちで2番目に近接する点を結びます．その結果，図中のすべての３角形が表示されます．これで，平面アイソゴンが構築されました．点Aを長方形の反対側の角にある次に近い点に結合した場合，2番目の対角線も描画する必要があり，単純なシステムにならない新しい点，つまりの交点が発生します．そのような点は仮定により許されません．アイソゴンの構築が完了したら，対称面と対称軸を表すすべての補助点と線を消します．
平面アイソゴンを構築する際に，異なる対称クラスから始めても，結果が同じになる場合があります．たとえば，図174の平面アイソゴン6は，元の点を正しく選択すれば，対称クラス(a / a)･m･6またはクラス(a / a):m･3から構築できます（図149を参照）．したがって，次の明らかな矛盾が発生します．平面アイソゴンは，その構造が基にした対称性と同じではない可能性があります．このケースは対称性の異なる5つの立方体の場合について以前に詳細に検討したときに起きた現象と同じです（図65）．アイソゴンを構築する際に，図形の物理的同価性を無視したため，明らかな矛盾が生じます．
これらの矛盾は，着色や陰影などの方法で図を処理することにより，完全に排除することができます．
この構築されたアイソゴンを「完全」と呼びます．これは，「不完全」なアイソゴンとの対比ですが，不完全なアイソゴンは，残りの線分が平面を凸多角形に分割するように特定の線分を削除して，完全なアイソゴンから導けます．図176ー178の番号36〜60は，この方法で取得された不完全な平面アイソゴンの例です．たとえば，図176の不完全な平面アイソゴン36は，平行四辺形の対角線を削除することにより，完全なアイソゴン8（図174）から得られます．アイソゴン40（図177）は，アイソゴン19（図175）から，菱形の短い対角線を削除して得られます．

典型的な平面アイソゴンから典型的な平面アイソヘドラisohedraを作るのは簡単です．平面アイソヘドラは，隙間なく平面を埋める同価なポリゴンで構成される平面無限の図形です．これらのポリゴンは，必ずしも平行ポリゴン（平行な辺を持つポリゴン）の一部である必要はないという点で，すでに検討されている平面ポリゴンとは異なります．平面アイソヘドラを構築するために，平面アイソゴンに対し，それらのエッジの中点を通る直線を描きます．直線は相互に交差した後，平面アイソヘドラの凸多角形を形成します． 例として，考えてみましょう． 図179.ここで細い線は，すでに遭遇したタイプのアイソゴンを示しています（図175の19）． 太い線は細い線の中点を通過し，細い線の辺に垂直であり，等辺６角形の系を形成します．

片面のみの平面one-sided-planeと両面のある平面two-sided-planeとはどのようなものでしょうか．
ただし，平面は離散平面でも連続平面でも良いことにします．

　　　　　　　　　   　a　　　　b　 　　　c　

図aと図bのどちらも，表面と裏面とでは性質が異なります．図aは，表面に＋電荷が帯電し，裏面にはー電荷が帯電した電気二重層の例です．表面に沿って並進を繰り返す，あるいは，連続移動しても，途中で表面の性質が裏面の性質に変わることはありません．従って，表裏の2面（両面）が存在し，その境界となる「面を一周する」縁があります．
1面（片面）しかない平面は，メビウスの帯やクラインの壺から連想できるように，表面に居ると思って表面をたどって移動していくと（並進すると），いつの間にか自然に裏面になってしまう，さらに，そのまま進むと初めに居た表面にもどります．面は表裏2面あるようですが，実は１つの同じ面なのです．従って境界は存在せず縁もありません．図ｃがその例です．
aは極性平面，　bは軸性平面，　ｃは捩性平面，と呼ばれます．

■片面帯（one-sided band）の対称性
特異点のない図形の対称性について

特異点（線，面）の概念は，有限図形の特別な変換のクラスに関して導入されます．図形は，この特別な変換クラス以外の変換では，不動点を持たないとします．特異点のない無限図形を得る最もシンプルな変換は，直線に沿った並進（有限距離の平行移動）です．この並進を無限回繰り返すと，直線のどの点も無限回繰り返されて，同価点が無限個並びます．そして，その直線（並進軸）は特異線になります．特異直線に加えて，並進により自分自身に重なる特異な片面（極性）面を持つならば，その図形は片面帯（one-sided band）と呼ばれます．「帯」や「ロゼット」などは，普通に使われる用語で概念の定義があいまいですが，ここでは完全に専門科学術語として用いていきます．

帯に必要な対称要素は並進軸
地下鉄通路や交差点の縁飾り

［要約］上に示したのはone-sided帯の例です．この例の横方向に並進がある縁飾りはone-sided面としたので裏面が存在しません．表面と裏面があり両者の間に対称操作が定義できるのはtwo-sided面です．

横１行の図形全体が，直線ABに沿ってaだけ動かすと（図形内の互いの位置関係を変えることなく），図形の１つがその隣の図形に一致するように，図形の全体は始めと違う新しい位置に動きます．直線ABを並進軸と呼びます．距離aの変位をしても，無限の図形なら如何なる変化も起きないので，望むだけ何度でも変位を繰り返せます．図形の変位はABの方向でも，逆の方向BAの方向でも同様の結果になります．すべての平行移動の集合は，この無限図形に対する並進群という新しい対称クラスを作ります．図形の行を並進した結果，初期位置と一致するような，最短の並進距離aを単位並進，あるいは，周期といいます．1次元の並進軸はaと表記します．これは無限の図形で存在できる対称要素であります．特異点がある有限や無限の図形は，並進軸を持つことができません．なぜならば，並進軸があるならば，図形の特異点は無限に繰り返され特異点ではなくなるからです．

対称要素aだけの帯（モチーフ部分図形は非対称）の例を示しました．帯を投影している紙面は，考察中の線形飾りの対称面ではない（one-sided）と仮定します．わかりやすくするため，一番上の図の帯の例で，片面が黒もう片面が白の３角形のカードボードをイメージしましよう．すべての３角形が黒側を観測者に向けています．紙面が対称面でないなら，図形は片面帯で裏面はありません．この帯のタイプは，並進軸に極性があります．つまり，（左右が対称ではない）AB方向とBA方向とでは性質が異なります．この図の帯を左から右へ追ってみると，常に，黒い3角形の先端から出現し，逆向きに追うと最も短い辺から現れます．並進軸の方向に極性があると，知らず知らずのうちに前進する印象を与えます．

 片面のみの帯面はone-sided band　といいます．
実際の面は裏表の2面あるのですが，表のみ（裏がない）という面をone-sidedといいます．
後に，two-sided bandも言及しますが，その場合の面は裏表があるので，
その間にひっくり返したり鏡映したりの対称操作が生じます．
帯とは，1次元の並進があるものを言います．

結論をいうと，片面のみの帯面の対称性は，以下の７つに分類できます．

■以下に示すいくつかの縁飾りは，上に示した７つの対称性のうちのどれに分類されるでしょうか？
実地に練習すると理解が深まります．

対称性により，パターンから受ける心理的な印象が異なります．
どのような場所で使うのが相応しいパターンでしょうか，ご想像ください．これらの図は，Shubnikov，Koptikの著書からです．

■両面帯two-sided band

帯とは無限に続く周期図形で，１つの特異平面と，その平面内の１つの特異並進があります．
片面帯one-sided bandはその特殊なケースで，特異平面に極性があり，その表面は裏面と異なります
[１つの表面しかありません]．
一般の帯では特異面は非極性であり，表裏の面を互いに重ねる変換が許されています．
許される変換のリストにこのような変換が追加されると，1次元の帯飾りに適用される対称類の数は，
片面帯の７つの対称類に加えて，非極性面をもつ両面帯の24の対称類が追加されます．
両面帯では，新しい対称要素；2回らせん軸が出現します．

■位数２のらせん軸
白と黒は3角形の表面と裏面を表します．

 ■両面帯の全部で31種類の対称類のパターンを，3角形モチーフの配列で表した一覧表を示します．
１，４，５，12，16，18，29の7種は，片面帯ですでに出現した対称類で，
残りの24種は，両面帯になって出現した対称類です．
（白面と黒面で表と裏を表しています．ドットのついた面は，表面と裏面が重なっている状態を表現しています）

帯のすべての対称類31種は，６つの対称要素６つの対称要素
$$a, 2, 2_{1}, m, \tilde{a}, \tilde{2}=\bar{1}$$　の独立な組み合わせで生成されます．
これら31個は，1次元の空間群と呼ばれます．

■両面帯に使われる以下のモチーフの対称性は？

■紙から対称帯を切りとる
以下の3つの例a,b,cの縁飾りは，紙をどのように折って切ったのでしょうか？
折り目になった線は対称面になるはずですね．

これまでは，特異平面を持つ片面の離散的（点の集合）な2次元周期図形（ネットワークパターン）のみを扱いました．これらの図形の裏側は表側とは異なると仮定しているため，対称変換によって表面と裏面を入れ替えることはできません．
今回扱う2次元の連続平面（つまり通常の平面）でも，表裏の2面が互いに同様な平面で，表裏がある場合と，表だけで裏のない片面のみ（極性）の平面の場合があります．
一見すると，これらの議論はばかげており，連続な無限平面図形（あるいは空間）では，ユークリッド平面と異なる平面を考えるのは無駄であるようにも見えます．しかし，私たちは，特性（特に，対称性）が互いに異なる平面の無限集合を考えるだけでなく，実際に作ることもできます．

この目的のために，すべての実表面は，一般に異なる物理特性を持つ2つの物体を分離する境界であるという事実を受け入れる必要があります．

■もっとも理解し易く，もっとも対称的な空間は，均一（一様）なもので，2次元空間の片面のみの面では，表面を均一な一色に塗り，裏面を黒く塗った平坦な厚紙のイメージです．このような図形の任意の点は，$$∞･m$$の対称性であることは容易に確認できます．極性対称軸$$∞$$は，表面に垂直に，至る点に通っていて，垂直な無数の対称面$$m$$があります．均一な片面の平面の対称記号は，対称性$$∞･m$$の点を連続並進$$(a_{0}:a_{0})$$したものだから，$$(a_{0}:a_{0}):∞･m$$と書けます．

■同様にして，均一な片面のみの面の他の対称類は，対称性$$∞$$の点を連続並進して得られます．
この表面の点には対称面がありません．この新しい平面空間を視覚化するには，両面の色が異なるように塗られた厚紙平面のすべての点で，一方向に均一に回転するのをイメージするだけで十分です．点の回転方向には2つの可能性があるため，このような空間には，左手型と右手型の2つのエナンショモルフ（対掌体）があります．新しい平面の良いモデルは，同じ方向に回転する円盤をランダムかつ均一に分布させたものです（以下の図）．円盤とそれらの間隔は十分小さく，個々の円盤を要素として分解できない観測者には，多くの要素の振る舞いの総和として効果を観測するしかありません．これは均質な理想平面でありその対称性を$$(a_{0}:a_{0}):∞$$　と記します．

■この片面平面の例から，対称性の低い平面に進むのは容易です．
この目的には，対称性$$n･m$$あるいは$$n$$の片面ロゼットの同価な図形の無限集合を用いるれば十分です．それらの方位を揃えて平面に配置し，図形をランダムかつ均一に分布させる．図形のサイズと間隔をゼロに漸近させると，極限で，対称性$$(a_{0}:a_{0}):ｎ･m$$，あるいは，$$(a_{0}:a_{0}):n$$をもつ均質平面を得ます．
［訳者注）$$∞$$回転軸は，対称性の極限で存在する．対称性を低下させたn回回転軸も存在する］

もし，初めのモチーフ図形に片面長方形，あるいはひし形をとれば，対応する媒質のモデルは以下の図のようになります．この構造の個々の要素を見分けられない観測者には，任意に選んだ各点Oは，長方形の対称性2･mをもちます．なぜなら，どちらの図形も，点Oの周りの180°回転，あるいは，平面$$m_1$$，$$m_2$$による鏡映は，全体として自分の上に自分を変換するからであります．

連続的な片面の例をもう一つ挙げてみましょう．両面を異なる色に塗った厚紙があるとします．平面上の直線に沿って一様な動きます．外部の観察者から見ると，厚紙は静止しているが，その対称性を調べれば，厚紙に垂直で，その運動方向に平行な，互いに平行な対称面の集合が存在することはすぐにわかる．この平面には，２次元連続体に常に存在する並進軸の他には対称性の要素は存在しない．
ここで，上記の考察が適用できる物理的に実在する平面や表面について，少し述べましょう（もちろん，自然界には理想的な平面は実在しません）．
滑らかな水の表面（例えば，光線を反射する能力を考慮した場合）は完全に等方性であり，明らかに対称性$$(a_{0}:a_{0}):∞･m$$を持っています．
光の偏光面を回転させることができる糖液の表面は，対称性$$(a_{0}:a_{0}):∞$$になります.
結晶の表面は，個々の原子（イオン、分子）の配置を考えるならば，不連続(離散的)な構造の平面パターンですが，その光学的，機械的性質を研究するならば，均質な平面として扱えます．
17種の対称性類が存在する（離散的な）平面パターンとは対照的に，片面平面連続体の対称類の数は非常に多い．これらの連続体の対称性記号を2列の無限列の形で以下に掲載します．

系列の最後の２つだけが完全に等方な平面に相当しています．他の記号は非等方の平面を記述します．記号$$(a_{0}:a_{0}):1$$はどの点も，並進軸以外にいかなる対称要素も持たない非対称平面に対応します．

ここでも，片面しかない平面を扱います．
半連続平面という概念がここで登場します．これは，例えば，横軸に沿っては連続的で，縦軸に沿っては離散的（デジタル化された）な平面のことです．最もシンプルな片面のみの半連続平面の例は，紙上に描かれた平行なストライプ（横縞）の系です．ストライプの断面の中点は明らかに片面のロゼット$$2･m$$の対称性を持っています．
半連続平面全体は，水平軸$$b_{0}$$に沿って，そのような断面を連続平行移動するのと，軸$$b_{0}$$に垂直な軸$$a$$に沿って，有限（とびとびの）平行移動することで得られます．したがって，図全体の対称性記号は$$(b_{0}:a):2･m$$と書くことができます．

１対のストライプをストライプ１つに置き換えても，図は同じ対称性を持っています．もし，等距離のすべてのストライプが同じ方向性を持っている場合，対称性$$(b_{0}:a):m$$の図形になります．
有向「2重ストライプ」の系は同じ対称性を持っています．

半連続平面の次の類は，構造要素としての幅広のストライプと幅狭のストライプで構成されたストライプです．
この断面の対称性は前の場合と同様に$$m$$ですが，対称面は垂直でストライプに平行ではないため，図全体の対称記号は，$$(b_{0}:a)･m$$になります．ただし， 記号･と：は，対称要素（特異平面に垂直）が，シンボル内の最も近い並進軸に，平行か，または垂直かをそれぞれ意味しています．

第4の対称類は，異なる幅の有向二重ストライプで構成されている場合で，その結果，縦対称面と横対称面の両方が構造からなくなります．これらのストライプの対称記号は$$(b_{0}:a):1$$，または，より一般化して，$$(b_{0}/a)1$$です．

第5の対称類は，隣接する有向2重ストライプが，2回対称軸によって相互に関連するものです．この類の対称記号は$$(b_{0}:a):2$$，または，より一般化して，$$(b_{0}/a):2$$です．

第6の対称類は，隣接する有向2重ストライプが，映進面$$~a$$によって相互に関連付けられています．対称記号は$$(b_{0}:a)･~a$$と書くことができます．

片面のみの半連続平面の第7で最後の対称類は，記号に，垂直な映進面~aを追加することによって5番目から，または水平面$$m$$を追加することによって6番目から得られます（鏡映面$$m$$は$$２$$回軸を通過することに注意しよう）．
対応する対称記号は，$$(b_{0}:a)･a:m$$，あるいは，$$(b_{0}:a):2･m=(b_{0}:a):2･a$$になります．

■まとめ：片面のみの半連続平面のすべての対称記号を以下の表の左端の列に書き出します．これらのうちで連続移動軸［記号$$b_{0}$$］を取り消し［$$b_{0}$$軸から下付き文字0を削除する］離散的移動にすると，片面のみの帯の対称性7種に帰着します．
したがって，片面のみの半連続平面は，無限の幅に引き出された通常の帯，あるいは，1つの連続した並進軸を持つ平面パターン（基本並進が無限に小さい）に他なりません．

対称性の理論は，実際にどのように発展してきたのだろうか？
この分野の歴史を見ると，純粋に幾何学的な側面に限っても，長期間かけて，対称性の概念が大きく変化してきたことがわかる．
ーーーーー
結晶点群の対称要素は：対称心；2，3，４，６回対称軸；回映軸；対称面；
結晶空間群の対称要素では，これらに加えて：並進；映進面；らせん軸
があり，これらの対称要素の集合が群（結晶点群，結晶空間群）を作る．
しかし，対称変換の要素をなぜこれらに決めたのでしょうか．その発展の歴史を振り返ります．
ーーーーー

■　始めは，反射（鏡映）のみを対称操作とみなした．

当初，研究者たちは幾何学的形態の対称性を，対称面による反射（鏡映）のみに限定していた．そのため，対称軸があっても鏡面がない図形は非対称とされました．また，単純回転軸を対称要素に加えたときも，回映軸を持つ図形は対称性のある図形の範疇に入りませんでした．これらの対称要素はすべて，有限図形の対称類を構築するために使用されました(Hessel, 1830; Gadolin; 1867)が，無限図形の対称性を記述するには不十分であることが判明しました．並進，らせん回転，映進の変換と，これらの操作に対応する新しい対称要素を導入する必要がありました．

■　第２種の対称変換を対称操作から除外する流派
ーーーーー
図形を変形せず剛体のように，回転，鏡映する対称変換は，直交行列で表現できます．その行列式は±１ですが，+1のものを第1種，-1のものを第2種といいます．第2種は，鏡映のように座標系を裏返す変換で，3次元の空間で+1の運動を-1の運動に変換するには4次元空間が必要です．例えば，右手と左手は鏡映対称で互いに一致させることができますが，実際に3次元空間内の+1の対称操作をしても，右手を左手に一致させることはできません．
ーーーーー

このように対称性の概念が大幅に拡張されたことで，対称性理論から第2種の変換（対称面での鏡映，回映，映進）を除外するという正反対の傾向が生まれました． この傾向の代表者は，Jordan（1869）とSohnckです．
また，対称性の研究において，ある種の対称面，単純回転軸，有限の平行移動を排除する妥協的な試みもありました(Bravais, 1850).

■　結晶点群と結晶空間群が完成

Fedorov (1891) と Schénflies (1891) は，最終的にすべての対称操作を統合しましたが，Jordanの無限小の運動 (並進と回転) は除外しました．このような操作は，彼らが研究対象にしている結晶の対称性と明らかに矛盾ると考えたからです．

そこで，限界対称性類にも特別な注意を払うことで，この除外されたギャップの解消をねらいます．

第１種と第２種の対称操作は，一見，非常に異なるように見えます．対称変換の概念に統合されたのだが，多くの研究者には，合同と鏡像の組み合わせがあまりにも人工的に見えるため，対称図形構築の統一原理を見出そうと注力しました．この問題に対する最も単純な解決策は Wulff（1897）とViola（1904）によって与えられました．科学の歴史ではよくあることですが，彼らは，対称面を基本的な対称要素として使うという最初のアイデアに戻ったのです．二人とも，3次元空間の有限図形のすべての対称変換は，3つ以下の平面（それらは対称面でなくても）での連続した反射（鏡映）に帰着できるということを証明しました．
WulffとViolaのアイデアを無限図形にも拡張すると，我々が認めたタイプの任意の対称変換は，最大4つの平面（それ自体は対称面である必要はない）による図形の引き続く反射に置き換えることができます(Boldyrev, 1907).

実のところ，この方法は，N.V.Belovが230の(Federov)空間群を導出したアルゴリズムに用いたものである(N.V.Belov,1951).

以下の図を参照ください：

●ある軸を中心に角度αだけ回転することは，その軸を通り，互いに角度α/2をなす2つの平面での引き続く反射（鏡映）に等価である．
●並進aは，距離a/2離れた平行な平面での引き続く2回の反射に等価である．
●回映は回転と反射からなり，3つの平面での引き続く反射に等価となる：２つの平面は回転軸で交差し，残りの平面は回転軸に垂直．

●映進面は，反射と並進からなり，３つの平面での引き続く反射に等価となる：2枚は平行で，3枚目は始めの2枚に垂直．
●らせん運動は，回転と並進の2つの動きに分解でき，4つの平面での引き続く反射に相当します：2枚は回転軸に沿って角度α/2で交差し，残りの2枚は互いに平行で，最初の2つの平面に直交する．

多数の反射を引続き繰り返しても，上に述べた操作 (対称面での1回反射も含む) と結果が変わらないことは，非常に簡単に示すことができます．また，平面での連続した反射によって，直線は直線に変換され，それらの間の角度と，直線上に記された目盛りの長さが保存されることも容易に納得できるだろう．

これは，上記のすべての変換において，図形はあたかも変形しない剛体であるかのように自分自身に変換されることを意味します．このような性質を持つ変換をアイソメトリック等長変換と呼びます．
等長変換に注目すると，次のようなシンプルで網羅的な定義を，3次元空間における幾何学的図形の対称性について与えることができます．
「対称的」とは，平面による1回または数回の連続した反射によって，それ自身と重ねることができるすべての(有限または無限)図形に適用される状態です．

特定の物体が，特定の対称性を顕わすか顕わさないかは，選択した特性によることで，内部構造にも関係があります．その意味では，対称性の定義には，外部と内部という2つの構造レベルの視点が残されます．

向きのある量の対称性

物理学や数学で使われる量には2種類あります。
大きさ（数値）だけで表現できるものと，大きさだけでなく空間における方向も示す必要があるものです．前者はスカラーと呼ばれ，後者は，ベクトル やテンソルと呼ばれます．例えば，質量，温度，密度などの量はスカラーで，（点の）変位，力，速度，電場などはベクトルです．ある物体の質量は，その物体が単位質量の何倍か，温度なら，摂氏スケールとして，温度の数値と符号（＋または-）を知る必要があります．
また，物体の変位を求めるには，その物体の移動距離cmと運動方向の両方を知る必要があるので，変位の大きさが長さで，運動方向を向いた矢印で示します．また，ベクトルは平行４辺形の法則に従って幾何学的に加算することが要請されます．
しかし，この要請にこだわり対象を制限するのは良くありません．
ベクトルの他にも，数値と方向をもつさらに広範な有向量を対象にする必要があるからです．有向量を決定する独立した（内部）パラメータの数が，その対称性と密接に関係していることを，だいぶ先になりますが取り扱うことになります．
では，有向量を表すのに使われる線分には，どのような対称性があるのでしょうか？この問いには多くの異なった答えがあり，仮定された条件の下では，そのどれもが正しい．例えば，４角柱プリズムの主軸は，周囲から切り離された状態で考えると，円柱と同じ対称性を持っています．同じ軸でも，プリズム全体と一緒に考えると，プリズム自体の対称性を持つことになります．
この例から，有向量は，図形の特異方向の存在と両立できるなら，任意の対称性を持てることがわかります．言い換えれば，有向量は，正多面体の対称類（図69の8列目）を除いて，特異点を持つ図形に許されるあらゆる対称性を持つことができます．
我々は，特に極限対称性の有向量に興味がある．というのは，物理学ではこの種の量が最も頻繁に登場するからです．

(a)
例えば、空間を移動する質点の速度は、静止している円錐の1枚のシート（∞･m）の形をしており、この量は、直線の断面で、「一方向」の矢印で表すことができます(図a)。これを完全に特徴づけるには、次のことが必要です。 (1)速度の数値(セグメントの長さ)、(2)空間におけるセグメントの向き（例えば、与えられた座標系とセグメントがなす角度を指定する）。(3) セグメントに沿った前方と後方の動きの違い、および、セグメントに垂直なすべての方向で動きに違いがないこと。このようなベクトルを極性と呼びます。電界強度は明らかに極性ベクトルです。
(b)
圧縮や引張を受ける円柱の軸方向の極性機械的応力テンソルの大きさは、圧縮や引張が常に両方向であるため、一方向きの矢印では表現できません。この種の方向量は、2つの矢じりが反対方向を向いた直線で表し（図b）、静止状態の円柱の対称性 m･∞:m を持ちます。
(c)
次に、軸性と呼ばれる方向量について説明します。例えば、軸を中心に回転する円柱の一様な角速度を表現したいとする。軸の速度と方向はこれまでと同様に直線で表すことができるが、回転方向は直線の矢印で表すことができない。そこで、回転方向を、回転の性質を示す循環矢印で表現する（図c）。このような量の対称性は ∞:m となり、円筒状の磁石の場合にはこれになります。磁石内の磁場は軸性ベクトルですが、磁石の両端の磁極は、実際には極性の極ではありません。
（d）
循環矢印がセグメントの両端で異なる方向を向いている場合は、新しい対称性∞:2の方向量（軸性テンソル）が得られます（図d）。この場合、対称面は存在せず、対称心もないので、量の右回りと左回りの形（反対の方向を持つ）を区別しなければならない（循環矢印の方向が反対になっている）。
この種の量の例としては、ワイヤーのねじれがあります。軸の方向、ねじれの角度（セグメントの長さに比例する）、ねじれの方向（循環矢印の方向で決まる）で指定される。結晶や溶液による光の偏光面の回転は、このクラスの量に属する。
極性と軸性の矢の組み合わせにより、回転する円錐の対称性∞を持つ極軸複合ベクトルが形成される（図c）。例えば、船のスクリュー、扇風機、プロペラなどの回転速度は、回転方向を示すセグメントの大きさ（速度に比例）と矢印の方向だけでなく、回転軸の「先端」の方向によっても決まります。後者の回転の質的な表示がない場合、その機械が正転で動作するのか逆転で動作するのかはわからないのである。
方向性のあるセグメントで表現可能な方向性のある物理量の対称性は、図a-eに示された5つの極限群によって網羅されている。2つのさらなる極限群（∞/∞･mと∞/∞）は、極性と軸性の（擬似）スカラー（無方向）量の対称性を記述するために使用される（図f,g）。スカラーの大きさに等しい長さの極球の任意の直径は、図bに図示されている種類の双方向矢印に対応し、軸方向のスカラー球では、図dに図示されている種類の双方向ねじり矢印に対応する。
すべての結晶学的直交群（および非結晶学的直交群）は、ピエール・キュリーによって最初に得られた上記の7つの極限群の部分群であることを思い出すべきである（図69参照）。

おわりに
我々は、特異点を持つ図形の対称性について説明することで、19世紀の第3四半期に開発された対称性理論の一部についての説明を終える。 科学の発展におけるこの段階は、ヘッセル、ガドリン Pierre Curie, Bravais, Fedorovの名前が挙げられます。後者は、特異点を持つ図形の対称性を”有限図形の対称性” と呼んでいるが、これはあまり良い言葉とは思えない。というのも、特異点をもつ図形の対称性に、無限の図形（双曲線、放物線など)もあるからです。

■3次元結晶空間群

一番有名なのが，3次元の周期的な空間（結晶空間）の対称性ですが，230種類の結晶空間群が数え上げられています．結晶（原子や分子による周期的な構造）の構造解析をしたり，その結晶構造を舞台として起こる現象の対称性を記述したりするのに使われ最も重要です．3次元の周期構造というのは，3次元の格子（3つの並進周期がある）構造を持つということです．

■2次元結晶群．層

2次元の周期のある構造を「層」と呼びます．無限に広がる平面で2つの独立な並進があります．「層」には，片面のみの「層」と両面をもつ「層」があります．私たちが壁紙模様の対称性（平面群）と言っているのは，片面のみの「層」の対称性で17種類あります．両面ある「層」の対称性は，全部で80種類あり，この中に，片面のみの「層」の17種が含まれます．
「層」の対称性など役に立たないと思うかもしれませんが，雲母などの層状の物質もありますし，半導体でも層状の構造があります．また，紙などは連続体ですが，紙の歪応力や力学定数を定義する時にも役立ち実用になるものです．

3次元の空間群の一覧を与える従来のやり方ではなく，次元を落とし，2次元の平面群17種でその構成の数学的原理をマスターすることが重要だと考えています．こうすれば，3次元や，さらに，4次元，5次元への拡張も自力で容易です．

■1次元結晶群．帯とロッド

1次元の並進しかない「層」の構造は「帯」と呼びます．帯にはやはり，片面のみの「帯」と両面ある「帯」とがあります．31種類の両面「帯」がありますが，そのうちの7種類が，片面のみの「帯」です．
もう一つの1次元の並進しかない構造に「ロッド」があります．結晶学的ロッドの対称群は全部で53種類です．［結晶学的というのは，回転やらせん軸が，2，3，4，6回に限られるという意味です］
「ロッド」の対称性も決して数学的遊びに留まりません．表紙の図に示したように，現実の物質が存在し，立派な応用があります．

31種類の両面「帯」の対称性から「ロッド」の対称性と重複するものを除いて，1次元の並進周期のある「帯」や「ロッド」の対称性は，全部で75種類です．

■結晶点群

並進のない図形［有限図形］の対称性を考えるには，変換で不動となる特異点が1点あるとして，この特異点の周りの対称操作が生成する群を数え上げます．これは全部で32種類の点群があります．

■色々な結晶空間群の関係

空間群，平面群，などは，その中に部分群として含まれる「並進群」を核として（並進で移動した点は同じと思え），点群に準同型に写像できます．

色々な空間の階層で考える群は，このように俯瞰的に見れば，たいへんすっきりするものです．

3次元空間の対称性への移行に備えて，これまでに研究されたすべてのタイプの群を一つの体系にまとめてみよう．記号$$G_{r,s,...,t}$$を使って，$$r$$次元幾何空間の（等長）対称群で，この空間の次元$$s,...,t(r>s>･･･>t)$$の（周期的，または非周期的）部分空間を同時にそれ自身に変換するものを表記する．この表記法で，片面ロゼットの点群（Ch.2）は，特異平面（2次元平面）とその法線（1次元空間）を自分自身に変換し，同時に特異点（0次元空間）を不変に保つことから，$$G_{3,2,0}$$，または$$G_{3,1,0}$$という記号を得る．
有限（または，無限）図形の点群$$G_{3,0}$$（Ch.3）は，3次元空間を自分自身に変換しつつ，単純に特異点を不変に保つ．
群$$G_{3,0}$$から群$$G_{3,2,0}$$に至るには，3次元図形の異なる平面断面を考えるか，ロッドの空間群$$G_{3,1}$$（Ch.6）の部分群として見つけることができる．両面平面によるロッドの長手方向の断面は，両面帯群$$G_{3,2,1}$$（Ch.5）の対称性を決定する．

後者からは，3次元空間を片面平面に投影し，片面帯の対称群$$G_{2,1}$$（Ch.4）に進むことができる．同様に，層の空間群$$G_{3,2}$$から，ネットワークパターンの空間群$$G_{2}$$（Ch.7）へと進む．これらの群と，そこから派生した層の対称群（$$G_{3,2,1,0}$$と$$G_{2,1,0}$$），片側ロゼットの対称群（$$G_{2,0}$$），直線の対称群（$$G_{1}$$），線分の対称群（$$G_{1,0}$$），点群（$$G_{0}$$）は，次のような方式で互いに関連しており，３次元空間群$$G_{3}$$（Ch.9）にも関連している：

この図式で，一重の矢印は部分群への移行；二重の矢印は断面や投影を表わしている．記号の前の数字は，離散的な結晶群の数に対応する．

同価点系

例として対称類$$\tilde{6} \cdot m$$を考察しよう．下図は対称類$$\tilde{6} \cdot m$$のステレオ投影図です．図aに記載されている対称要素は主軸$$\tilde{6} $$（$$6$$回回映軸），鏡映面3枚$$m$$（太い線分），紙面内にある$$2$$回軸３本（基円上に両端が現れている），対称心$$\bar{1}$$があります．ステレオ投影は地図作りでも用いられますが，地球の表面の点を平面（基円内）に投影する方法でした．地球を北極側から見ていると想像しましょう．ステレオ投影の〇印は，北半球の表面にある点，×印は南半球にある点の投影像です．

球面上の１点に対称類（点群）の対称操作を作用させ生じる点の全体（同価点系，あるいは正則点系）を考察します．元の点を球面上で動かすと，他のすべての点も動きます．生じる同価点系の点の数は，元の点が対称要素の1つに当たるまで変わりません．

図aは，一般点に対称操作を作用させて生じた同価点のステレオ投影図です．全部で12個（＝対称操作の数＝群の位数）の同価点が生じています．

図bは，特殊位置（鏡映面上にある場合）に元の点がある場合で，ステレオ投影で生じる同価点の数は6個と半減しました．

図cは，特殊位置（$$2$$回軸上ある場合）に元の点がある場合で，ステレオ投影で生じる同価点の数は6個です．やはり半減しました．

図dは，元の点が3回軸と3つの対称面上にある場合で，同価点の総数は6分の1になります．

図eのように，元の点が，すべての対称要素が交差する特異点にある場合ならば，対称操作により生じる点はすべて重なってしまうので，ステレオ投影で生じる点も1点です．この点の多重度は12．

1つの点に重なる同価点の数を，その点の多重度と呼びます．
同価点の系（正則点系）で，点の多重度とその点の同価点数の積は一定で，群の位数になります．（対称類$$\tilde{6} \cdot m$$の位数は12）

図a,b,c,d,eの正則点系を構築する際に，対称類は同じままであるという仮定がありました．しかし，図b,cの点系を比較すると，これらは異なる対称性を持っことがわかります：例えば，図bの系には3回軸があり，図cの系には6回軸があります．このように一見矛盾しているように見えるのは，まだ点自体の対称性を無視しているからです．点は〇で表現されていますが，実際には〇ではなく，図a,b,c,d,eの5つの系で，点の対称性は全く異なっています．

図aでは，点（一般点と呼ぶ）はどの対称要素にも乗っておらず，その多重度は1で，完全に非対称である．図bの系では，元の点は対称面m上に位置し，点の対称性は鏡映対称mです；図cの系の点は，２回対称を持ちます．図dでは，点の対称性は3･mを持ちます．

以上，対称類~６･mを例にして，適当に選んだ1点に対称操作を作用させて，同価点の系（正則点系）を作りました．これを，単純点系といいます．これに対して，複合点系というのは単純点系の組み合わせで作れます．

それぞれの種類の点は，独自の同価点系を形成し，異なる系に属する点は互いに同価ではありません．
複合系の記述には，点の多重度の相対比が重要です．例えば，多重度が2，6，12の3つの単純系からなる複合系があったとしましょう．この相対比は，1，3，6となる．この数は化学組成において重要な役割を果しています．すべての分子は，数学的近似において「点」と見做せる原子またはイオンよりなりますから，同価な原子（イオン）は１つの単純形をつくり，構成原子（イオン）の相対比はそれらの原子（イオン）が占める位置の対称性の制約となります．

注意が必要なのは，元の点の位置が固定されるのは，対称軸の交点，つまり球の中心にあるときのみということです．この場合にのみ，その対称類でただ1点の同価点系を得ることができます．
それ以外の場合は，元の点の位置は，その形で点の数を変えることなく，無限に存在します．言い換えれば，2点，6点，12点の正則系が無数存在します．

図72に示した正則点の系を構築する際には，すべての点の系において対称類が同じままであるという仮定から始めた．図72b,cの系を比較すると，これらは異なる対称性を持っていることがわかる：例えば，図72bの系には3回軸があり，図72cの系には6回軸があります．このように一見矛盾しているように見えるのは，まだ点自体の対称性を無視しているからであり，これらはいずれも誤って円として表現されている．実際には，4つの系では，点の対称性は全く異なっています．図72aでは，点はどの対称要素にも乗っておらず，その多重度は1に等しいので，完全に非対称である．図72bの系の点は二回対称で，対称面上に位置し，それぞれ対称性mを持つ；図72cの系の点は対称性2を持つというように異なっている．点の対称性については，後で詳しく議論する．

以上，図72の例を用いて，（適当に選んだ1つの点を繰り返すことで生じる）単純な点の系がどのように作られるかを示した．単純なシステムから，複雑な複合システムに移行することは難しくありません．後者の場合，球体上または球体内にいくつかのタイプの点があります．
それぞれの種類の点は，同価な点の独自の系を形成し，異なる系に属する点は互いに等しくない．
複合系の記述には，点の相対的な数が重要な役割を果たすが，その数がどのようにして得られるかを見てみよう．例えば，2点，6点，12点の3つの単純系からなる複合系があったとする．この相対数は，これらを2の共通因子で還元して，1，3，6となる．後述するように，この数は化学において重要な役割を果たしている．というのも，すべての分子は，数学的近似において「点」とされる同価な原子またはイオンの複雑な対称系とみなすことができるからである．
この計算により，例えば，対象とする対称性類について，2種類，3種類，4種類の非等価な点を含む複合系の相対数を表3に示す．

(Picture)

物質は分子で構成されており，分子は原子，イオン，ラジカルなどで構成されていることはよく知られている．科学的な化学が始まった当初から，同一の性質を持つ化学分子の部分は同一の（対称的な）位置を占めると考えるのが通例であった．この考え方は，少数の化学元素を扱うことが多い有機化学では特に有効であり，次のような場合には同一元素の原子を識別する必要がある．
例えば，CH3COOHという式で表される酢酸の分子では，炭素記号Cが2回現れるが，この2つの炭素原子の違いを明示するためである．
酢酸の性質を調べると，1つの分子には4つの水素原子Hが含まれており，そのうち3つの水素原子は化学的性質が等しいが，4つ目の水素原子は異なる．
酢酸の式では，記号Hが2回使われているが，そのうち1回のHには添字3がついている．
ラウエがX線回折を発見し，結晶や分子の構造解析法が開発された後，分子や結晶格子の構造単位が対称的に配置されていることが実験的に確認され，構造化学や結晶化学への対称性理論の応用は広大な分野となった．
原子（ラジカル）を点（あるいは図形）で仮に表すと，分子は点（図形）の規則的な（単純，あるいは複合的な）系である．分子の対称類と，同じ性質を持つ原子の種類の数がわかっていれば，対称類と矛盾しない化学式を事前に決めることができる．
例えば，ある化学分子が，性質の異なる2種類の原子AとBから構成されており，その対称性が$$\tilde{6} \cdot m$$であることがわかったとする（図72）．この対称性類を満たす化学式はすべて候補となる．
言い換えれば，２元系化合物$$A_{n}B_{m}$$の式に含まれる係数nとmをすべて計算しなければならない．同一の原子が分子内の単純系の点を占めると仮定すると，係数nとmは，複合系を形成する単純系の点の相対比となる．相対比の表（表3）を見ると，この場合のすべての公式を簡単に書き出すことができる．

$$A_{1}B_{1} ; A_{1}B_{2} ; A_{1}B_{3} ; A_{1}B_{6} ; A_{1}B_{12}$$
これらの式は，化学的に等価な原子が構造的に等価でない場合，すなわち，A型とB型の原子がそれぞれ構造的に区別される場合に；$$A_{n1}, A_{n2}, \cdots , A_{ni} , B_{m1}, B_{m2} , \cdots , B_{mj}$$に分かれていると，より複雑な状況になる．この場合の2元化合物$$A_{n1}A_{n2} \cdots A_{ni} B_{m1}B_{m2} \cdots B_{mj}$$は，再分割された原子のそれぞれが単純系を占めている．

平面群

平面群から層の空間群へ

2次元平面には，裏表があると思いますか／ないと思いますか？
2次元とは厚み方向の次元のない世界ですから，その世界には，表面や裏面の区別はありません．しいて言えば，片面だけ（1面だけ）の平面です．この2次元平面を私たちの住む3次元世界に置いたとすると，表側面と裏側面の区別が生じます．

周期的な2次元平面とは，面内に２つの独立な並進ベクトル$$a，b$$があり，この２つのベクトルで挟まれる平行4辺形を単位胞（単位タイル）として，平面を敷き詰めた構造です．周期的な2次元平面の対称性（平面群）は17種類ありました．いわゆる17種類の壁紙模様のことです．2次元平面（壁紙模様）は片面のみの世界で考えたものです．

我々の3次元の世界の中で，2次元の平面を見たときに，表面と裏面の区別が生じますが，このように表裏のある2次元平面を「層」と呼びます．

層というのは，3次元の世界に置かれた2次元平面ですので，層には表面と裏面があります．

層（表側と裏側のある面）の2次元周期的模様の対称性（空間群）は,80種類あります．もちろん，80種類のうちに片側のみの面の対称群17種類は含まれます．

片側のみの面の対称群17種類から，どのようにして80種類の空間群が導けるのでしょうか．

第１の方法は，層の内部（層に含まれるような）に，対称心，鏡映面（あるいは，映進面），2回軸（あるいは，2回らせん軸），などの，位数２の対称操作を導入し，片面の世界を他の面の世界に写像することです．つまり，
片面のみの壁紙模様の17種類の平面群と，層の内部に置いた位数2の対称群との直積で「層の空間群」を生成する方法です．

第2の方法は，2次元（片面）平面群の生成元を，表面と裏面との間の変換が起こるものに置き換える方法です：回軸対称軸を位数２のらせん軸に，あるいは鏡映面を映進面に置き換えることです．

こうして，17種類の平面群から，80種類の層の空間群を導くことができます．

層の（空間群）対称性をすべて導くことは，30年代にドイツの科学者；Hermann，Weber，Alexanderらによって完了しています．
層に対する空間群など，何に応用できるのかと思う方もおられることでしょう．層の対称性（空間群）は，表面や界面の記述に用いることができます．結晶学では液晶構造，ドメイン界面，双晶，エピタキシャル接合の研究に，物理化学では単分子層や薄膜の研究に，生物学では膜構造やその他の生体組織の研究に応用できます．また，建築芸術においても， 透かし彫りの格子構造，覆い，フェンス，看板などのデザインに応用できます．

それにもましてこの概念が重要なのは，層に対する空間群の内部構造を理解することが，群の拡大理論に直結し，反対称群などの概念の構築の基礎になることです．

3次元空間の対称性への移行準備のめに，これまでに研究されたすべてのタイプの群を統一的なスキームに統合しましょう．記号$$G_{r,s, \cdots ,t}$$は，$$r$$次元の幾何学空間の（等長）対称群であり，かつ，この群が，$$s, \ldots ,t\left( r>s> \cdots >t \right) $$次元の（周期的，または，非周期的）部分空間を，それぞれの中に変換するとします．この表記法で，片面ロゼット（第2章）の点群は，記号$$G_{3,2,0}$$（または，$$G_{3,1,0}$$）となります．なぜならば，この変換は，特異平面（2次元空間）と，それに垂直な（1次元空間）を，それぞれの中に変換し，同時に，特異点（0次元空間）を不変に保つからです．
有限（あるいは，無限）図形の点群$$G_{3,0}$$（第3章）は，3次元空間を自分自身の中に変換する一方，特異点だけを不変に保ちます．
群$$G_{3,0}$$から，3次元図形の異なる断面を考慮するか，棒の空間群$$G_{3,1}$$（第6章）の部分群を使って，群$$G_{3,2,0}$$に到着しました．両面平面による棒の（縦）断面は，両面帯群$$G_{3,2,1}$$（第5章）の対称性を決定します；後者からは，3次元空間を片面平面に投影して，片面帯$$G_{2,1}$$（第4章）の対称群へ進みます．
同様に，層群$$G_{3,2}$$から，網目パターンの空間群$$G_{2}$$（第7章）に移行します．
これらの群と，タイル（$$G_{3,2,1,0}$$と$$G_{2,1,0}$$），片面ロゼット（$$G_{2,0}$$)，直線（$$G_{1}$$)，線分（$$G_{1,0}$$），点（$$G_{0}$$）対称群は，以下のスキームによって，互いに，かつ，3次元空間の対称群$$G_{3}$$（第9章）と関係づけられます：

図中，一重矢印は部分群への移行；二重矢印は断面，または，射影を示します．記号の前の数字は，離散的な結晶群の数．

両面連続面（連続面）の対称類の求め方は，片面連続面で行ったのと同様です．すなわち，両面ロゼット対称下の任意の点を選び，この点にロゼットの特異対称軸に垂直な軸$$a_{0}$$に沿って連続移動を行い；得られた直線を，やはりロゼットの特異軸に垂直，あるいは，任意の角度をなす並進軸$$b_{0}$$沿って連続移動します．$$b_{0}$$軸はロゼットの特異軸に垂直で，並進軸$$a_{0}$$とは任意の角度（例えば，直交）をなしている．
初期点の対称性が$$n:2$$の場合，連続体の記号は$$\left( a_{0}/b_{0} \right) :n:2$$，あるいは，$$\left( a_{0}:b_{0} \right) :n:2$$となります．両面ロゼットの対称類の数は無限なので，両面平面の連続体の対称類の数も無限です． 
対称性$$\left( a_{0}/b_{0} \right) \cdot m: \infty \cdot m$$を持つ両面平面の例は，全方向に一様に引き伸ばされた薄いゴム製フィルムです．このようなフィルムの各点は，個別に見ると，$$m \cdot \infty :m$$［$$ \infty $$軸，垂直と水平な対称面，水平な2回軸］を持っています．同じフィルムを一方向に引き伸ばした場合，対称性$$\left( a_{0}:b_{0} \right) \cdot m:2 \cdot m$$を持ち，このようなフィルムでは，各点の対称性$$m \cdot 2:m$$，すなわち，直方体の対称性を持っています．
両面平面の半連続体は，帯の軸に対して垂直または斜交する平面内の方向に，両面帯の対称性を持つ直線を連続移動して得ることができます．帯の対称類の数が31であることから（図92参照），両面半連続平面の対称類の数も同じです．
対称性$$pmmm$$（図92,19）の帯から作られた半連続体の例として，互いに等間隔で平面内に張られた平行な線を挙げられます．
線の軸上の各点は，$$mmm=m \cdot 2:m$$の対称性，すなわち，両面帯19の個別図形の対称性を持っています．
線の間隔は，帯の図形間の距離に対応しています．線に沿って一方向に電流を流すと，半連続体の対称性は，帯の対称性$$pm2m$$（図92の5）になります．
図92（$$p12/m1$$）で考察した線の系の磁場は，両面帯28の対称に対応する半連続体の対称性を持っています．

「層」と壁紙模様の関係は，「帯」と縁飾の関係と似ています．壁紙［2次元］模様から層［3次元中の2次元］に移行するには，特異平面が極性であるという要請を緩和する必要があります．「層」を特徴づける2つの条件は：特異平面（片面および両面）の存在［簡単のために，層の特異平面は常に水平とします］と，２つの並進軸です．この定義を受け入れるならば，壁紙模様の概念は層の概念に含まれることになり，層に特異点がないという要請もこの定義から導かれます．あらゆる種類の層の対称性をすべて導くことは，30年代にドイツの科学者；Hermannヘルマン，Weberウェーバー，Alexanderアレクサンダーらによって行われました．層の対称性は，結晶学では液晶構造，ドメイン界面，双晶，エピタキシャル接合の研究に，物理化学では単分子層や薄膜の研究に，生物学では膜構造やその他の生体組織の研究に応用されています．建築芸術においても， 透かし彫り格子構造，覆い，フェンス，看板などのデザインに応用できます． 

層の対称要素 

壁紙模様は片面だけなので，模様のある表側面から裏側面に模様を移す「反転」という対称要素は存在しません．これらの対称要素は，層の内部に存在し，対称心，水平面内にある位数２の対称軸（単純回転，らせん回転），水平な対称面や映進面などです．古典的な対称原理に留まる限り，未発見の新しい対称要素を層に見出すことはありません．しかし，層の対称性を研究することは，対称性の概念自体を拡張し，層の反対称群や3次元（有限および無限）図形の対称群の導出に繋がります．

層の対称類の導出．表現と表記法

既に導いた2次元平面群の17種類に加えて，層のすべての対称類の導出は，これら17種類の中から同一の壁紙模様をペアにするか，あるいは，生成元に「反転」の対称要素を追加することです．まず，各類に水平な対称面を追加すると，層の17個の両面対称類ができます．新しい対称要素を導入した結果，特異平面の単位面積当たりの基本図形の数は，もし，複数の古い図形から作られた新しい図形同士の融合や絡み合いがなければ，明らかに2倍になります． 
層の対称類の表現は，帯で先に使用した方法と同じで，図184－187にその単位胞を示します．図に表示されているのは，観察者方向に向いた面で，黒い3角形が見えれば，その裏側は白い3角形，白い3角形が見えれば，その裏側は白い3角形です．点のある３角形は，「表側面」と「裏側面」が同じ両面3角形です． 
両面層の空間群の非座標記号は，片面層の空間群の場合と同様です（図149参照）．シンモルフィック群の対称記号を得るには，2次元並進群$$( a/b)$$ ,$$(a:b)$$ ,あるいは，$$\left( \displaystyle \frac{a+b}{2}/a:b \right) $$を，有限図形に対応する対称群に「乗じる」必要があります（図69参照）．点群の対称要素に層平面内の並進を「乗じる」ことになり，いくつかの派生対称要素が生じます．並進群と点群の記号の間には，これらの群の対称要素の相対方位を表示する記号（$$･$$あるいは$$:$$）が置かれます． 
どの場合（図187の70-72, 74の層を除く）でも，点群の記号で，最初に左に書かれてい対称要素は，層$$( a,b) $$の平面と並進群の記号で括弧内の最後に書かれている並進軸に，平行（$$ ･ $$），または，垂直（$$:$$）です．
このような状況下で，点群の記号は必ずしも標準形ではないが，図69と同じ分離記号（$$･$$あるいは$$:$$）が用いられます：
$$m:2=2:m, m･2=2･m, m:2･m=m･2:m, m:4･m=m･4:m, m･3=3･m, m:3･m=m･3:m$$, $$2:3=3:2, m･6=6･m, m:6=6:m, m:6･m=m ･6:m$$.
非シンモルフィックの層群の対称記号中で，$$2$$回回転軸の一部または全部が2回らせん軸$$2_{1}$$に置き換えられ，対称面$$m$$が映進面$$\tilde{a}, \tilde{b}, \tilde{ab}=\tilde{n}$$［最後の平面では，並進$$\left( a+b \right) /2$$は単位格子の対角方向］に置き換えられています．層の空間群は全部80で，そのうち45はシンモルフィック，35は非シンモルフィックです．

80種類の層の対称類

層の個々の対称類について詳細を記述することはしません．なぜならば，図形の正則系の投影図（図184～187）から，基本的事項は直接見てとれるからです．これらの投影図には，対称要素は全く表示されず，図形（３角形）の相互配置のみが示されています．図184-186の細い線は，層の単位胞を区分しています．図187では，辺を挟んで隣接する２つの3角形で単位胞は構成されます．層を作るには，隙間も重なりもなく単位胞を並進させて平面を埋めます．
さらに，表11には，図149と同様な軸方位で，層の空間群の非座標表示と座標表示（国際表示）を比較掲載しました．読者は，図149と図69の群の表示を参考にして，両面層の対称要素の配置を投影して描いてみるとよいでしょう．

結晶空間（＝3次元の離散体）のブラベー格子は，14種類ある．ブラベー格子とは，結晶の内部構造の並進性とその対称性により，結晶構造を分類する概念である．
結晶空間は，無限に広がる3次元周期をもつ離散体（デジタル化された空間）なので，
①並進性（並進群で記述）：並進で移動できる点（格子点）はすべて同価．
②格子点自体には，点群で記述される対称性がある．

結晶空間の全域に作用し，これを不変に保つ対称操作の集合が，その結晶空間の結晶空間群であり，結晶空間群の対称操作は，結晶点群と並進群の対称操作の組み合わせである．もちろん，並進群だけで結晶空間群の部分群を作る．結晶空間全域に作用し，結晶空間を不変に保つ結晶点群の対称操作は，当然，局所の格子点自体が従う対称操作でもある．

注）
並進群：3次元結晶空間には，互いに独立な基本並進ベクトル$$a, b, c$$があり，$$n,m,l$$を任意の整数として，1次結合$$n･a+m･b+l･c$$を格子点といい，すべての格子点の集合（無限集合）を格子という．格子は並進群の図的表現でもある．
結晶点群：結晶空間の対称操作（変換の前後で空間を不変に保つ操作）で，かつ，空間の1点を不動（特異点）にする対称操作の全体が作る群．

無限に広がる結晶空間で，並進で移動した位置はすべて同値（格子点はすべて同値）と考えると，無限個ある格子点を1点に還元でき，結晶空間群を結晶点群に還元することができる．

■石英，岩塩，ダイヤモンドの結晶構造の例．

石英
低温水晶α-quartzの構造を観察すると，図面に垂直な３回らせん軸（風車のような記号）が，正3角形の格子点に分布しているのがわかる．これらの3回らせん軸は，1つの空間群のなかでは，すべて右まわりか左まわりに統一されている：空間群の記号で$$P3_{1}21$$（右），$$P3_{2}21$$（左）．
石英の組成はSiO₂だが，この図に描かれているのはSiだけで，Si位置の紙面レベルからの高さを，黒丸，白丸，半黒丸で区別している．紙面に垂直方向の周期をc=1とすると，黒丸（+1/3レベル），白丸（-1/3レベル），半黒丸（0レベル）である．
紙面の矢印は，水平面内にある2回軸で，その高さレベルの数字が記されている．
ーーーーーーーーーーーーーーーーーーーーーーー　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

岩塩
上図はNaCl結晶の単位胞を示す．Naイオン（黒丸）とClイオン（白丸）が，立方体の辺に沿って，あるいは，面の対角線や体対角線に沿って，交互に並んでいる．黒丸と白丸は，イオンの種類が異なるので互いに同価点ではないが，両者のペアは同価点になれる．例えば，白丸だけをペアの代表（格子点）と考えると面心格子Fになっていることが理解できる．
NaCl結晶構造の対称性は，並進（格子）だけではない．黒丸，および，白丸位置の対称性（点群）は，ともに$$ m\bar{3}m $$（非座標記法では$$\tilde{6}/4$$）である．この点群のステレオ投影図を，格子点である白丸の位置に配置したものを上図に示した．NaCl結晶構造の空間群は$$Fm\bar{3}m$$である．
－－－－－－－－－－－－－－－－－－－－－－－

ダイヤモンド
上図に示すのは，ダイヤモンドの結晶構造である．これは，2つの面心立方格子$$F$$を，立方体の体対角線の方向に1/4だけ相対的にずらし重ねたものを考え，両方の面心立方格子の格子点に炭素原子を置いたものである．両方の面心格子の格子点をペアで代表点とすると考えれば，ダイヤモンド構造の格子は，やはり，面心立方格子$$F$$であることがわかる．

2つの面心格子の複合
ダイヤモンド構造の場合，２つの面心格子の格子点には同価な原子があり，２つの面心格子（黒と赤）は，例えば，映進面dにより互いに変換し合う．黒の面心格子を，$$d$$で鏡映し，かつ，$$(1/4)a＋(1/4)c$$だけ平行移動すると，赤の面心格子に変換され，この逆も成立する．ここで現れた$$d$$をダイヤモンド映進面と呼ぶ．
面心格子の格子点の点群は$$\bar{4}3m=3/\tilde{4}$$で空間群は$$F\bar{4}3m$$であるが，ダイヤモンド構造では，2種類の炭素原子がこれらの２つの副格子の格子点を占めていて，ダイヤモンド構造の空間群は$$Fd\bar{3}m$$である．

空間群$$Fm\bar{3}m$$と$$Fd\bar{3}m$$には，共通な部分群$$F\bar{4}3m$$を含み，点群$$m\bar{3}m$$と$$d\bar{3}m$$（格子を法とする点群）は，互いに同型な点群である．結局，空間群$$Fd\bar{3}m$$は空間群$$Fm\bar{3}m$$から，鏡映面$$m$$を映進面$$d$$に置き換えて得られる．

■非座標式標記法（ロシア式）と座標式標記法（国際式）

結晶空間群$$\mit\Phi $$は，並進群$$T$$と結晶点群$$G$$（あるいは，並進群$$T$$を法として拡張された結晶点群$$G^{T}$$）の積で作られます．
結晶点群$$G$$を用いた場合に生じる空間群をシンモルフィック，拡張された結晶点群$$G^{T}$$を用いた場合に生じる空間群を非シンモルフィックといいます．
空間群の標記法は，基本的には，群の生成元を列挙することです．まず，格子のタイプを表す記号を冒頭に置き，続いて結晶点群の生成元を並べます．国際的な標記法では，点群の生成元を，座標系の$$x, y, z$$に対応する順番で配列しますので，これを座標式標記法と言います．ロシア式標記法では，前の対称要素の方位とそれに続く対称要素の方位の関係を標記します．直前の対称要素の方向に対して，続く対称要素の方向が，直角な場合は（$$:$$），平行あるいは同一面内にある場合は（$$･$$），直角以外の角度で斜交する場合は（$$/$$）を，間に置きます．国際記号はInternational Tableで用いられているもので，この標記法れが標準ですが，群の構造情報が詳細明瞭に表現できるロシア式は，空間群の理論を扱うのに欠くことはできません．
230種類ある結晶空間群を分類する7つの晶系の内から，Orthorhombic晶系（慣用的に”斜方晶系”と呼ばれる）をとり上げ，説明します．

■Orthorhombic晶系の部
単純格子のタイプは，互いに直角な$$a, b, c$$軸よりなる．単位胞の形は，直方体（レンガのような形）です．

「帯」（バンドやリボン）とは，1次元に周期のある2次元面の呼び名とすることにします．
帯には表面と裏面の2面がありますが，それは，我々が３次元空間にいて，帯の2次元面を見るからです．
帯自体が厚みの次元のない2次元世界ですので，２次元世界にいれば表面も裏面もありません．

帯の模様の対称性を考察するにあたり，1面(片面)帯と2面(両面)帯に分けて，それぞれの空間で空間群を調べます．

■1面(片面)帯の７種の空間群
1面帯(周期は1次元)を記述する空間群は，以下の7種類あります．

  1面(片面)帯の７つの空間群
赤記号は対称要素．緑のモチーフは非対称単位．
1面帯の模様を，モチーフの分布で表現している．

片面帯の対称操作には，周期$$a$$の他に，映進面$$\tilde{a}$$，鏡映$$m$$，2回軸$$2$$が可能です．
周期$$ a $$は除き，他は皆，位数２の対称操作です．このほかに対称心（反転）$$\bar{1}$$があるように思うかもしれませんが，反転操作は，裏表のある3次元以上の世界で可能な操作で，片面だけの2次元平面には存在しません．
これらの組み合わせで生成される群は，上記の7種類になることがわかるでしょう．
もし，位数２の対称操作以外（例えば，4回軸など）の対称操作が加わった集合を考えると，帯（1次元だけ周期がある）の世界では，群を生成できません．

■下図のイスラム模様は，
Ahmed Saad　Analysis of the arabian geometric patterns　より引用

Ahmed Saad作品より引用

このイスラームの模様の作品には，９本の片面帯からできています．

各帯には，局所的な，4回軸，6回軸，8回軸が見られます．しかしながら，このような位数が２より高い対称操作が，1次元周期の世界の全域に作用することはできないので，群の生成に寄与することはできません．結局，これらのイスラームの模様の空間群は，以下のようになります．

イスラームの模様の特徴は，局所的に，対称性の高いロゼットが嵌め込まれていることです．空間群で記述すると，これらの局所的な対称性は反映できないので残念ですが，これらの1面帯から受ける印象は，高次元の影を見るような不思議な魅力があります．

■演習
説教壇の階段手摺模様に見られる片面帯の空間群は，7種類のうちのどれでしょうか．

Analysis of the arabian geometric patterns 　より引用

球の密な充填（積層）．結晶学と構造工学における重要性

球の3次元充填でこれがが最密であるというKepler予想は肯定的に証明されました．この予想の証明は難問で400年もかかりました．しかし，ここでは，その構造が最密であるという断定はあえて避け，密な充填というレベルにとどめます．さらに，ここで考察するのは，厳密に言うと，球のランダムな充填は検討外で，球の最密配列層の積層（規則的）の範疇に留めていますです．そのため，充填ではなく積層という言葉を使うようにしています．

（注）ケプラーはまた、球を敷き詰めたときに、面心立方格子が最密になると予想した。 この予想はケプラー予想と呼ばれ、規則正しく敷き詰める場合に関してはカール・フリードリヒ・ガウスによって早々に証明されたが、 不規則な敷き詰め方に関しては、400年もの間未解決の問題であった。ケプラー予想は1998年に、トーマス・C・ヘイルズによって、コンピュータを駆使して解決された。wikiより引用－－－－
現在，離散体（＝結晶空間）の対称性は，結晶学や固体物理学で関心を持たれていますが，その理由は，すべての結晶は離散体であるからです．しかし，この問題は，他の学問分野や工学分野からも少なからず関心を集めています．特に，建築美術では，空間的な構造を計算する方法がなく，「平面的な問題」にとどまっていましたが，今日では，離散体の対称性理論は，建設工学に応用されるようになりました．ここでは，レンガ積みやトラス構造などや，物体を最も密に詰めるという問題に係わります．隙間や重なりなく平面を充填したり分割する様式や球の密な充填様式は，N.V. Belov（1947年）とToth（1953年）の問題提起が参考になります．

一見すると，球を高密度に充填する方法は1つしかないように見えますが，実際には無限にあります．これを理解するために，同一の球を，それぞれの球が6つの球に接するようにして1層並べてみましょう（図195のa）［パチンコ珠をトレィに並べた様子です］．この配置は平面では，最も密度の高いものになることがわかっています．これを，第１層として層の積み重ねを考えます．第2層の球を，第1の層の上に，最も密な配置となるような唯一の方法で配置することができます：第2層の球の 1 つは，2の位置または 3の位置の窪みを占めることができますが，これらは，どちらも同じ結果になります．次に，第3層を，出来上がった2層系の上に積み重ねるわけですが，2つの方法があります：第3層の球は，第1層の球と同じ位置を占めるか，第2層の球が2の位置にある場合は3の位置（第２層の球が3の位置にある場合は２の位置）を占めるかです．このようにして得られた2種類の3層系の違いは，第3層の層の球を投影した時，第1層の球と一致するかしないかにあります．
球の中心を平面に投影すると3種類の位置ができますが（図195のb），どのような積み重ねであろうとも，この3つの位置以外に球は存在しないことがわかります．したがって，球の最も密な充填は，数字の1,2,3からなる記号で表すことができ，これらの数字の有限または無限の列のなかで，同じ数字が2つ続かないようにします．明らかに，この条件を満たす3つの数字の配列様式は無限です．したがって，球の最密充填は無限にあります．無限に続く数字の列が，ある同一の有限の組み合わせを周期的に繰り返すならば，その構造は対称的（周期的）です．そうでなければ，同じように球を高密度に積み重ねても，少なくとも層に垂直な方向には，非対称（非周期的）な構造になります．例えば，12312 12312 12312....は，12312という組み合わせが周期的に繰り返されていることから，対称的（周期的）な5層構造と定義されます．この列の2つの数字の間に，1つの余分な数字を挿入すると，構造の並進対称性が一気に崩れます．
対称的（周期的）な積層において，すべての球（半径は等しい）の構造中で占める位置は，互いに同価ではないことに注意しましょう（同価性は3層構造の場合にのみ当てはまります）．多層構造のすべての球には，構造のすべての層ではないが，異なる層にある並進同価な球の無限集合があります．非対称な積層では，同じ球は同じ層の同じ位置にしか入りません．
球の最密充填は，どのような対称群になるでしょうか．ある対称的な積層に対応する数字の配列を見ましょう．数の列が，左から右に読んでも、右から左に読んでも同じなら，構造には対称面となる層平面が存在します．例えば，列1213121312.....では，対称面は層2と層3にあります．もし，順方向と逆方向の読み取りで，数の並びが違っているなら，構造に層（水平方向）に沿った対称面はありません．水平方向の対称面を持つすべての構造は，同じ６方対称（$$P6_{3}mmc$$）を持っています． 例えば，6方対称の２層積層12（図196のa）は，このような対称性です．

対称要素と球の積層構造の投影図を重ね合わせ，第1層の球を実線で，第２層の球を破線で示します．第1層から第2層への変換は，紙面に垂直な螺旋軸$$6_{3}$$と$$2_{1}$$の回転（単位胞への投影はこれらの軸のよぎる点で，それぞれ羽付きの黒い6角形とレンズで表示），反転（紙面から$$c/4$$上にある白丸），並進$$c/2$$を伴う回映（破線）の垂直な映進面（破線で表示）が担う．これらの要素に加えて，この投影図には，垂直方向と水平方向の対称面が描かれています（後者は1番目の層の球の中心と一致しています）．水平な対称面間を通過する水平な2回軸は，投影図には表示しません．
水平な対称面を持たない球配列（立方体の3層配列を除く）は，すべて3方対称性を持つ．例えば，12132の3方対称の5層積層は，空間対称群が$$P\bar{3}m1$$である（図196, b）．与えられた投影図は，各層1,2,3の球をそれぞれ長短の点線と実線で表しています．
4番目の層の球は1番目の層の球と，5番目の層の球は2番目の層の球と，投影が一致しています．紙面上にある対称心（小さな白い円）は，3番目の層の球の中心と接点に一致しています．同じ中心で，4番目の層の球（紙面上）は2番目の層の球（紙面より下）に，5番目の層の球は1番目の層の球に映されます．
この投影図には，対称心のほかに，垂直方向の対称面（実線），映進面，垂直方向の単純軸と回反軸$$3, \bar{3}$$が示されています．水平方向の対称軸$$2, \bar{2}$$は，投影されていません．

図196のcは，立方面心格子の対称性を持つ3層構造の投影図です$$Fm\bar{3}m$$．図193のcとは対照的に，このグループの対称要素は，垂直軸$$3$$に沿って図面上に投影されており，点群$$m\bar{3}m$$のステレオ投影の中心は，球の中心と一致しています．1番目の層の球の中心は紙面の中心にあります．1番目の層の球から2番目の層および3番目の層の球（図中に数字で示されている）への移行は，垂直な螺旋軸$$3_{1}, 3_{2}$$で回転させることによって行うことができます（それらの投影は，羽付きの小さな黒い3角形で示されています）．また，対称心（レベル$$c/6$$および$$c/3$$の小さな白い円）で反射させることもできます．2番目の層と3番目の層の球の中心は，投影図に対応する数字で示されているように，レベル$$c/3$$と$$2c/3$$にあります．さらに，この投影図では，レベル$$c/2$$にある対称心が，2番目の層と3番目の層3の球と映進の垂直面を結んでいます．群$$Fm\bar{3}m$$の対称要素の一部は，投影図には表示されていません．

立方および6方の高密度充填の3次元モデルを図197のa,bに示します．2層積層では、位置3（図195のa参照）が球で占められておらず，層に垂直に走る構造的なチャネルが，6次の$$6_{3}$$の3方向のらせん軸とその方向で一致している．立方積層には，構造上のチャンネルがありません．この2つの積層は，ほとんどの化学元素の結晶構造や，多くの無機化合物や鉱物の構造における陰イオンの積層に対応しています． 

フェドロフの平行多面体（Parallelohedron）と非対称要素立体（Stereohedron）

Параллелоэдры(Parallelohedra)и стероэдры(Stereohedra) Федорова

一つの平行多辺形で，平面を隙間なく埋めるという問題は，3次元空間に対しても提起できます．空間では，平行多辺形の役割は，平行多面体が担っています．代表的な平行多面体には，立方体，2つの底面を持つ６角柱，菱形12面体，細長い菱形12面体，立方8面体（切頂８面体）の5種類があります（図198）．隣接する平行多面体の面が完全に一致するように，同一の平行多面体を充填し，すべての平行多面体が平行になるようにすると，重なりや隙間のない空間充填ができます．5つの典型的な平行多面体から，それを伸ばしたりずらしたりすることで，無限の派生平行多面体を得ることができます．
立方体から変形させると，直方，および，斜方の平行多面体，６角柱から変形させると，斜方の6角柱などになります．平行多面体にある種の対称性を持たせれば，一般的には非平行に配向した等価な部分に分割できます．分割された部分をStereohedron非対称要素立体と呼びます．３次元空間における非対称要素立体は，2次元平面におけるプラニゴン（非対称要素）Planigonに相当し，非対称要素立体は，3次元離散体の最小不可分な部分を表しています．それは，さらに小さい等価部分に分割することはできませんが，それらの部分は直交変換によって互いに変換し合います．ここでは，すべての非対称要素立体のカタログを作ることはせず，いくつかの例を挙げるにとどめます．
平行多面体が対称心を持たない斜方の平行六面体（対向面は異なる色とする）である場合，その図形を等価部分に分割できず，それ自体が非対称要素立体です．平行六面体の中心に対称心がある場合は，その図形は2つの非対称要素立体に分割することができます．立方体は，対称面によって48個の非対称要素立体に分割できます（図189のa参照）．E.S.Fedorovが離散体（結晶空間）の230種類の対称類を導出した際に，Stereohedron非対称要素立体は大きな役割を果たしました．球などの最密充填の問題は，非対称要素立体や平行多面体による空間充填の問題に還元できる部分もあります（B.N.Delaunay, 1934参照）．

図198

2次元結晶空間の中の対称操作で，1点を不動の特異点にする対称操作の作る群は10種類．
$$1, m, 2, 2mm, 3, 3m, 4, 4mm, 6, 6mm$$

-------------------------------------

$$2mm=2⊗m$$
$$3m=3⊙m$$
$$4mm=4⊙m$$
$$6mm=6⊙m$$

$$6=3⊗2$$
$$4=2○4(mod2)$$

 --------------------------------
$$6mm\left\{ \begin{array}{@{\,} c @{\, } }
\left\{ \begin{array}{@{\,} c @{\, } }
\vartriangleright 6\left\{ \begin{array}{@{\,} c @{\, } }
\vartriangleright 3 \\[0mm]
\vartriangleright 2
\end{array} \right. \\[0mm]
\supset m
\end{array} \right. \\[0mm]
\left\{ \begin{array}{@{\,} c @{\, } }
\vartriangleright 3m\left\{ \begin{array}{@{\,} c @{\, } }
\vartriangleright 3 \\[0mm]
\supset m
\end{array} \right. \\[0mm]
\supset 2
\end{array} \right. \\[0mm]
\left\{ \begin{array}{@{\,} c @{\, } }
\vartriangleright 2mm\left\{ \begin{array}{@{\,} c @{\, } }
\vartriangleright 2 \\[0mm]
\vartriangleright m
\end{array} \right. \\[0mm]
\supset 3
\end{array} \right.
\end{array} \right. $$

$$4mm\left\{ \begin{array}{@{\,} c @{\, } }
\left\{ \begin{array}{@{\,} c @{\, } }
\vartriangleright 4\left\{ \begin{array}{@{\,} c @{\, } }
\vartriangleright 2 \\[0mm]
○4(mod2)
\end{array} \right. \\[0mm]
\supset m
\end{array} \right. \\[0mm]
\left\{ \begin{array}{@{\,} c @{\, } }
\vartriangleright 2mm\left\{ \begin{array}{@{\,} c @{\, } }
\vartriangleright 2 \\[0mm]
\vartriangleright m
\end{array} \right. \\[0mm]
\supset 2
\end{array} \right.
\end{array} \right. $$


$$3m\left\{ \begin{array}{@{\,} c @{\, } }
\vartriangleright 3 \\[0mm]
\supset m
\end{array} \right. $$


■対称群を系統的に見る
$$\begin{array}{|c|c|c|c|c|}
\hline
\begin{array}{@{\,} c @{\, } }
次元数 \to \\[0mm]
周期軸数 \downarrow
\end{array} & 0 & 1 & 2 & 3 \\[0mm]
\hline
0 & G_{0,0}=1 & G_{1,0}=2 & G_{2,0}=10 & G_{3,0}=32 \\[0mm]
\hline
1 & \times & G_{1,1}=2 & G_{2,1}=7 & G_{3,1}=75 \\[0mm]
\hline
2 & \times & \times & G_{2,2}=17 & G_{3,2}=80 \\[0mm]
\hline
3 & \times & \times & \times & G_{3,3}=230 \\[0mm]
\hline
\end{array}$$


■2次元のブラベー格子
２次元のバラベー格子は5種類

２次元のバラベー格子は5種類

\documentclass[a4paper,10pt]{jarticle}

\usepackage[dviout]{graphicx}

\begin{document}

$$\begin{array}{|c|c|c|c|c|}
\hline
単位胞の形 & 晶系 & 非座標式表示 & 座標式表示 & 格子 \\[0mm]
\hline
正方形 & 正方格子 & \left( a:a \right) & p & \begin{minipage}[b][79pt]{77pt}
\includegraphics[width=77pt,height=79pt]{2次元結晶学_001.bmp}
\end{minipage}
\\[0mm]
\hline
正3角形 & 6方格子 & \left( a/a \right) & p & \begin{minipage}[b][86pt]{89pt}
\includegraphics[width=89pt,height=86pt]{2次元結晶学_002.bmp}
\end{minipage}
\\[0mm]
\hline
面心長方形（菱形） & 直方面心格子 & \left( c/b:a \right) & c & \begin{minipage}[b][78pt]{80pt}
\includegraphics[width=80pt,height=78pt]{2次元結晶学_003.bmp}
\end{minipage}
\\[0mm]
\hline
長方形 & 直方格子 & \left( b:a \right) & p & \begin{minipage}[b][84pt]{81pt}
\includegraphics[width=81pt,height=84pt]{2次元結晶学_004.bmp}
\end{minipage}
\\[0mm]
\hline
斜交4辺形 & 一般格子 & \left( b/a \right) & p & \begin{minipage}[b][73pt]{88pt}
\includegraphics[width=88pt,height=73pt]{2次元結晶学_005.bmp}
\end{minipage}
\\[0mm]
\hline
\end{array}$$

\end{document}