平面群

壁紙（2次元）の繰り返し模様の対称性は，17種類の平面群に分類されます．17種類の平面群の表を掲載しておきます．それぞれの対称群の説明はこれからするのですが，先にこの表を提示するのも，役に立つことでしょう．
この表で，採用した平面群の表記法は，国際記号とロシア式記号です．(”Симметрия”, Шубников и Копцикより)
今日，国際記号が普及していますが，ロシア式記号は，群の生成元を表示しているので，群の構造が良くわかる特徴がありますから，群の理論的研究に適しています．両者の対応を表にまとめておきます．

国際記号$$p1$$，ロシア式記号$$(b:a)1$$

対称性が並進（格子の周期）以外に何もないパターンの例です．

 図中に同じ部分が繰り返し出てくる様子を調べます．例えば，上図のような格子が見つかるでしょう．このように格子周期以外の対称性がない場合は，単位胞タイル（オレンジで囲んだ平行４辺形）の中身全部が非対称要素（モチーフ）です．

平面群の記号で，格子を表す部分は，国際記号で$$p$$（なんの条件もない平行４辺形），ロシア式記号で$$(b/a)$$［$$b$$軸と$$a$$軸が直角でない一般的な角度で交差］と表します．点群の対称性の記号は何もないので$$１$$と記載します．

これが，もっとも簡単な平面群（第１類）です．
以下の図のように平行４辺形を変形したものも，この対称性を持っています．

この対称性に属するエッシャーの周期的な作品もいくつかあります．
私は，ハロウイン魔女を作って見ました．

 美しい幾何学p.68

 第2回目（第2類）は，国際記号$$pg$$，ロシア式記号$$( b:a)･\tilde{a}$$の対称性です．
$$g$$はglide plane (映進面)の意味，$$\tilde{a}$$は並進成分が$$a$$軸方向に沿った映進の意味です．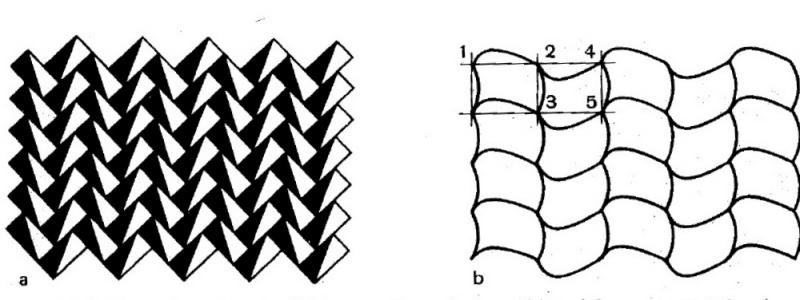  

上図の模様は，どちらも同じ対称性で，横軸方向に映進があります．縦軸（上下方向）方向には映進はありません．

上図は有名なエッシャー作品（邂合）です．この図は縦方向$$b$$軸に沿って，映進$$\tilde{b}$$がありますので$$( b:a)･\tilde{b}$$，先の例を90°回してみたものと同じ対称性に属します．
■映進操作の説明は以下で行います．

美しい幾何学p.93-95

表紙の写真はネットからお借りしたエジプトの模様です．
(今回の対称性は繰り返し模様の第３類）
この対称性は，国際記号で$$p2$$，ロシア式記号で$$(b/a):2$$　と記述されるのもです．作り方は，紙面に垂直な2回回転対称軸が，横軸（水平方向）に配列している状態が基本になります．その1次元の状態は，$$(a):2$$と表示します．周期的に（横軸$$a$$方向に）2回軸（赤で染めている）が1次元配列をしている状態なら，それらの2回軸の中心に新しい2回軸（白抜きにしている）が生じることは，図を見ているとわかるでしょう．

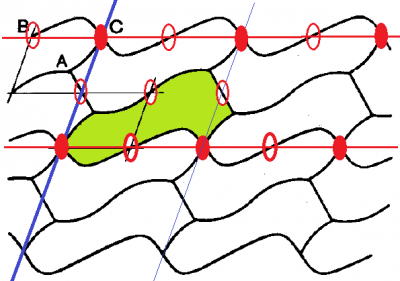
さて，この１次元の帯を，$$b$$軸(青い直線）に沿って繰り返し平行移動して2次元のパターン$$(b/a):2$$が得られます．$$b$$軸と$$a$$軸の交差する角度は，直交とは限りません（一般的な角度でOK）［注）ロシア式記号$$(b/a)$$は一般的な角度の意味．直交する場合は，$$(b:a)$$と書くのが決まりです］．この場合，非対称要素（モチーフ）は単位胞タイルの1/2(例えば黄緑色に着色した部分）です．

この対称性の繰り返し模様はエジプトの模様でよく見られます．私たちも知らず知らずのうちに，このような模様をエジプトの民芸で見ているのでしょう．この模様を見たときなんとなくエジプト風を感じませんか．

表紙の模様もそうですが，次の模様も同様です．

これらのエジプトの模様では，$$b$$軸と$$a$$軸は直交していますが，これはたまたまのことで，軸を直交させたとしても全体の対称性は変わりません（対称性が上昇するわけではないので記号を変える意味がありません）．［注）2回回転対称軸が存在できる格子は，$$a$$軸と$$b$$軸が斜交しているもの（平行4辺形）でかまいません．もちろん直交してもかまわないのですが，条件のゆるい斜交している方を選びます］　次の図は，上のエジプトの模様を私が改造して，一般的な角度で$$b，a$$の軸が交差する模様に変えてみました．対称性は同じです．

今回は，平面群の第４類の説明です．この類は，直交する２つの映進面がありますので複雑です．
映進面が１つのパターン$$pg$$の例を参照ください．

以下のペルシャのパターンが，$$pgg2$$の繰り返し模様の例です．

国際記号で$$pgg2$$，ロシア式記号で$$(b:a):\tilde{b}:\tilde{a}$$と書かれるものです．
［構成方法１］ 
①　2回対称軸が$$a$$軸方向に周期的に配列した1次元構造（図の1番上の行にあります）；　
この対称性は$$(a):2$$
②　この1次元構造を，$$b$$軸（$$a$$軸に垂直）に沿って映進$$\tilde{b}$$すると，2次元のパターンが得られます．　　対称性$$( b:a) :\tilde{b}:\tilde{a}$$
(注) 1次元構造$$( b) :2$$を映進$$\tilde{a}$$で繰り返し広げても同じ構造が得られます．
［構成方法２］
互いに直交する２つの映進面$$\tilde{a}$$，$$\tilde{b}$$が作用すると，
このパターン$$( b:a) :\tilde{b}:\tilde{a}$$が得られます．

上記の2つの構成方法を等しいと置くと，$$\tilde{b}:\tilde{a}=2 \odot \tilde{a}$$となり
これは，点群$$2m$$に同型な，拡張された点群であることがわかります．

（注）$$\odot $$
２つの直交する映進面$$\tilde{a}$$と$$\tilde{b}$$の組み合わせは，
交差する直線（不動線）がありますが，2回軸$$2$$と映進面$$\tilde{a}$$の組み合わせは，
互いに平行で交差しません．
記号$$ \odot $$は交差しない対称操作の組み合わせであるときに用いる記号です．
(注）拡張された点群 
$$\tilde{b}:\tilde{a}$$の組み合わせも，$$2 \odot \tilde{a}$$の組み合わせも，それらの対称操作を繰り返すと
並進の成分が生まれます．そのため，格子分だけ移動したものは同値としないと点群になりません．このような拡張された点群は，格子を核として写像すると点群に帰着できます．この場合は群$$2m$$と同型になります．

イスラムデザインの美しい壁紙をご覧ください．

pinterestからお借りたこのデザインは，Aziza（カタールのドーハを拠点とするアーティスト）によるものです．彼女は神聖幾何学とイスラムのパターンを研究しています．https://artofislamicpattern.com/#/6

この模様はとても魅力的で，イスラム模様の特徴がよく出ています．
色のグラデーションがとても素敵なのですが，ここでは幾何学の話をするので，色の区別ができない眼鏡をかけたと思って色は無視します．

この壁紙の成り立ちを，表紙の図に示しました．この図の平面群（全部で17種類あります）は，$$p4mm$$と記号で書かれるものです．このような繰り返しパターンは，モチーフ（非対称要素）となる図形を，$$p4mm$$の対称操作で配置し構成されます．

壁紙模様で，まず目につくのは周期（格子）で，これを平面群の記述の先頭に書きます．この例では，記号で$$p$$と書きました．2次元のブラベ格子のタイプは$$p$$（plain＝単純）と$$c$$（c-centred＝ｃ面心）の2つしかありません．そして，17種類の壁紙の対称性のうちの15種類が単純格子に分類されます．2次元の格子のタイプ分類（2次元のブラベ格子は5種類）は，前回の「ネットワーク・パターンの分類」で始めたところです（参照ください）．

この壁紙模様の例では，すぐ，黒い正方格子が目につきます．しかも，正方形の中心にも格子点のある（$$c$$面心格子）複合格子のように見えます．しかし，対角線の方向に目を配ると，一辺の長さが$$1/\sqrt{2}$$　になった，赤い正方格子（$$p$$格子）が見えてきます．

始めに気づいたc面心格子（黒い格子）は「正方形」の対称性ですし，後で気づいた$$p$$格子（赤い格子）も「正方形」の対称性です．$$c$$面心格子を作れたように見えましたが，黒い格子を$$1/\sqrt{2}$$に縮小し45°回転すると赤い格子と同じものになります．正方格子のは$$p$$格子だけで，$$c$$面心格子は存在しないことがわかります．

 この繰り返し模様のモチーフ（最小の非対称要素）は，赤い格子の1/8（黒い格子の1/16）の直角２等辺３角形です．このような3角形の模様付きタイルを作れば，そのタイル８つで赤い格子$$p$$格子の単位胞内を作ることができます．出来上がった単位胞を並べれば，無限に繰り返す壁紙模様が出来上がります．このモチーフは非対称要素と呼ばれるように対称性のない最小タイルです．

最後に，平面群の対称性の記法で，格子タイプ$$p$$に続く$$4mm$$は，格子点の対称性を記述する点群の記号です．
（注）平面群と点群の関係を正確に言うと：平面群は，格子を法とする準同型写像で点群に帰着します．

繰り返し模様の対称性の第５類は，
国際記号で$$pmg2$$，ロシア式記号で$$(b:a):m:\tilde{a}$$ 
（$$a$$の上に~を載せた記号$$\tilde{a}$$を,Texがつかえない場所では~$$a$$のように書くことにします）

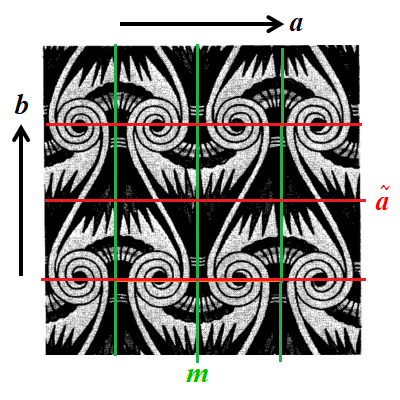
 垂直な帯$$(b)･m$$を，水平方向のa軸に沿った映進面$$\tilde{a}$$で繰り返すことで得られる．
対称性の記号は$$(b:a):\tilde{a}:m$$と記述できる．上図に示したのはこの対称性のパターンの例です．このパターンの中で，つながっている２つのコイル状の曲線に注目しよう．一つは，s字の形になり，他方は逆s字の形になっている．2回回転軸は紙面に垂直で，S字曲線の中心とコイルの中心を通っています．尖った葉を束ねて尖った葉の先端が上を向いたり下を向いたりしています．
帯の対称性$$(b)･m$$は，$$(b):2$$　とも書けるし，映進面$$\tilde{a}$$は2回軸を面内に含むので，この2次元のパターンの対称性は，$$(b:a):m:\tilde{a}=(b:a):2･\tilde{a}$$　と記述できます．

束ねた葉の尖った先端を上に向けたり下に向けたりしているパターンは，蓮の花の円錐形のデザインでエジプトの伝統模様に見られます．

以下の模様も同じ対称性です．

（注）拡張された点群$$2･\tilde{a}$$は，格子分並進したものは同値と見なすことにすれば，点群$$2･m$$に同型です．映進面$$\tilde{a}$$の中に2回軸が含まれるので，記号$$ ⊙ $$を用いる必要はありません．

今回は第6類の対称性です．格子のタイプが$$p$$（単純格子）ではなく，面心格子$$c$$が現れました．国際記号で$$cm$$，ロシア式記号で$$(a/a)/m$$です．

ハート（対称性$$m$$）のモチーフが水平方向に$$a$$で繰り返され，垂直方向に$$b$$で繰り返されています．しかし，長方形（横$$a$$，縦$$b$$）の頂点にハートを配置しただけでは足りません．長方形の中心にも配置します．これは面心格子ですが，$$c=(a+b)/2$$の新しい周期ができています．このcを加えて$$(c/b:a):m=(a/a)/m$$と書かれます．古代のマウレタニアのパターンとのことです(Owen Jones)．

以下の中国のパターンも同じ対称性です(Owen Jones)．

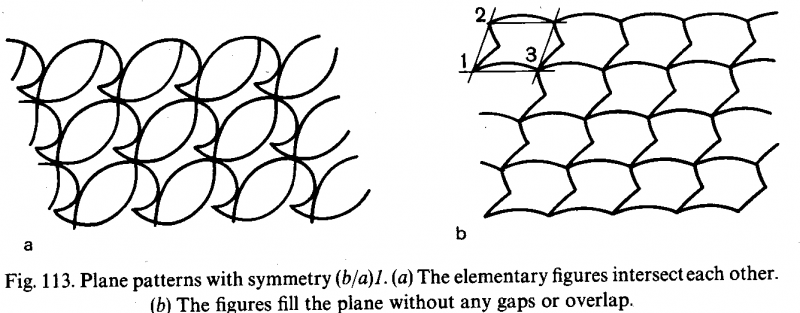
等価なパーツで平面を隙間なく充填するこの対称性をもつパターン

 以下の例（pixtaのサイトからお借りしました）は，このような対称性です．

日本の伝統模様の青海波などはこの対称性です．以下参照

美しい幾何学p.88より

第７類の壁紙模様の対称性は，国際記号で$$pm$$，ロシア式記号で$$(b:a):m$$です．この対称性の模様は分かりやすく非常に単純なものになります．

表紙の画像（pngtreeの無料画像サイトからお借りたイスラム模様）は，この対称性に分類できます．以下の画像は，ちょっと見るとこの対称性のようですが，反S字のコイルになっているので鏡映面$$m$$はありません．

以下の模様も，$$(b:a):m$$の対称性の例です．日本の伝統模様のサイトからお借りしました．釘抜繋ぎという模様らしい．

]

一般的な，パターンは，上の図のようです．
長方形の単位胞の半分が非対称領域のタイルになります．

17種類の壁紙模様の対称性の第８類は，
国際記号で$$cmm2$$，ロシア式記号で$$(a/a):2･m$$　です．

点群$$2･m$$の図形を，並進の大きさは等しいが対称面(赤線)には斜交する軸（青線）$$(a/a)$$に沿って並進させて得られるので，$$(a/a):2･m$$と記述できる．
あるいは，面心格子$$c$$［黒いダイヤに注目すると面心格子が見えてきます］で，同じ点群$$2･m$$の図形を並進させると得られる．
菱形格子［単純格子］$$(a/a)$$の単位胞の面積は，面心格子［2格子点を含むものが単位胞］$$(c/b:a)$$の単位胞の面積の1/2です．

$$(c/b:a):2･m$$
$$(c/b:a)$$が面心格子を表し，$$m$$は赤い鏡映面を表し，鏡映面の交点には紙面に垂直に2回軸がある．

$$(a/a):2･m$$
菱形格子（単純格子）$$(a/a)$$を採用すると，このように記述できる．
これら両者の記号は同じ対称性を表現している．$$(c/b:a):2･m＝(a/a):2･m$$

このような対称性で，等価なパーツだけで平面を隙間なく（重なることもなく）充填するパターンは次のようなものです．釣鐘の形が非対称要素（モチーフ・タイル）で菱形の単位胞（単純格子）は２つの釣鐘型からなり，面心格子の単位胞は，４つの釣鐘型からなります．

次の例は，この対称性の日本の伝統文様「菱文（ひしもん）」です．この図はネットからお借りしました．

■平面群の記号，$$(c/b:a):2･m$$や$$(a/a):2･m$$の記述に使うのは，群を定義する最小の対称要素［群の生成元］だけ記載します．下図を見てください．完成した平面群の対称要素のなかには，生成元だけでなく，細い赤い線［映進面］や白抜きの赤い2回軸が生じています．

菱形格子と，面心格子のそれぞれの単位胞を下図に着色して置きました．

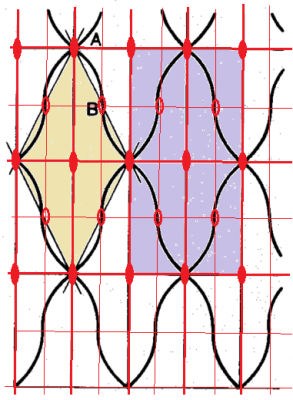
今回は壁紙模様の第９類で，国際記号で$$pmm2$$，ロシア式記号で$$(b:a):2･m$$です．

対称性$$2･m$$の単位胞図形を長方形の格子$$a$$軸，$$b$$軸で並進してパターンができます．
以下の図は，この対称性のパターンとはわずかに違うのですが，どこが違うかわかりますか？
間違い個所を見つけてください．

 例えば，ダイアモンドを頂点とする長方形が単位胞ですが，この単位胞の中身の対称性は，どうでしょうか．中心に2回回転軸はありますか？確かに，垂直に鏡映面はあります．よく見ると，コイルの巻き方は鏡映対称を満たしていますが，2回回転対称とは矛盾します．従って，厳密に言うと単位胞の対称性は$$2:m$$でなく$$m$$ですので，パターンの対称性は，$$(b:a):m$$，国際記号では$$pm$$の繰り返し模様になっています．
それでは，厳密にこの対称性$$(b:a):2･m$$である別の例を探してお知らせください．日本やイスラムの伝統模様で見つかると良いのですが．不思議なことになかなか見つかりません．自分で作った方が速いかもしれません．

もし，先に掲載した例を修正するなら，渦巻きコイルでなく同心円に変更します．蔓の重なり方も紙面上下の立体感を失くして平面内にある様に変更します．表紙の図のようになります．ただし，蔦の重なり方を修正していないので，2回対称を満たしますが，鏡映対称に矛盾します．両者を満たすには，蔦の重なりが，平面上にある様に修正する必要があります．しかし，あまり面白いデザインではないので，もっと良いデザインに皆様ご挑戦ください．

繰り返し模様の対称性の第10類は，国際記号で$$p4$$，ロシア式記号で$$(a:a):4$$．単位胞の図形の対称性$$4$$を，直交する軸（従って，正方形のメッシュが格子）に沿って並進して得られるパターンで，$$(a:a):4$$で記述される．以下の２つのエジプト模様の例は，ちょっと見るとこの対称性のようですが，厳密には，この対称性を満たしません．

問　どこがいけないのか間違い探しをしましょう．

 解答

左のパターンでは，背景にストライプがありますので，4回対称軸は2回対称軸に低下します．そして，格子は直交している必要がなくなり，対称性は$$(a:a):2=(b/a):2$$になります．
右のパターンでは，コイルの渦巻きは2回回転対称のようですし，花は花弁が10枚のようですから，単位胞の中身は全体として4回回転対称になりません．

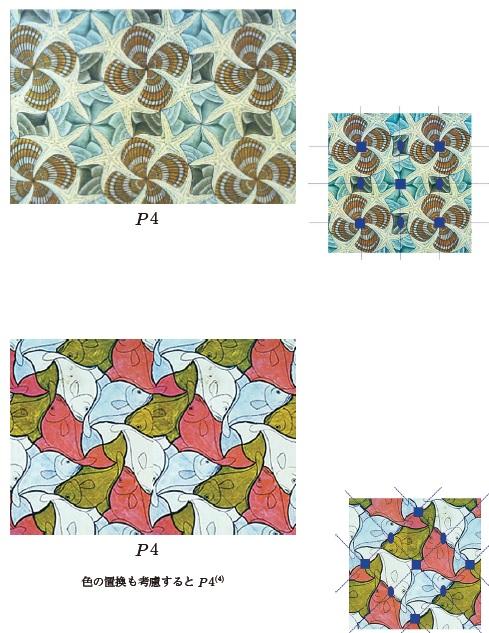
等価なパーツが隙間なく平面を充填するパターンの例
この対称性のパターンは，正方形の格子並進，4回軸がありますが，鏡映面はありません．モチーフ（非対称要素）は単位胞の1/4(例えば薄桃色)です．パターン全体を見ると，それぞれのパターンには対掌体（風車の回り方が逆なもの：chiral，enantiomorphs）が存在します．

この対称性のエッシャー作品の例を以下に示します． 

美しい幾何学p.99より

対称性の第11類です．国際記号$$p4gm$$，ロシア式記号$$(a:a):4･\tilde{a}$$

このパターンは，4回対称の単位胞を，２つの等価な互いに直交する映進面で繰り返し広げて得られる．
縦，横の映進面$$\tilde{a}$$は，群$$4･m$$に同型な，法による点群$$4･\tilde{a}$$の4回軸を通る．

 上の図はこの対称性のエジプトのパターンと言いたいが，厳密に見ると4回軸はなく２回軸になっている．
（間違い探し：４回対称性を破っているところを探しなさい）

 縦，横の太い赤線は鏡映面．細い赤線は映進面．映進面の交点に4回回転軸がある．太い線の交点には2回回転軸が生じている．

単位胞の面積は，非対称要素（モチーフ）が8個で出来ている面積に等しい．

以下の図は，pngtreeのサイトから借用したもので，今回の対称性の図の例です．

繰り返し模様の対称性の第12類は，$$4･m$$の図形を正方形単純格子$$(a:a)$$で並進させて得られる．

この対称性は，国際記号で$$p4mm$$，ロシア式記号で$$(a:a):4･m$$と記述される．
この対称性のパターンの例は

非対称要素（モチーフ・タイル）は，単位胞の1/8です．

この対称性の日本の伝統模様はたくさんあります．
例えば，以下の七宝つなぎなどです．イスラムの模様との交流もあったと思われます．

\begin{array}{|c|c|c|c|c|c|c|c|c|c|}
\hline
\textgt{国際記号} & p1 & p2 & pm & pg & cm & pmm2 & pmg2 & pgg2 & cmm2 \\[0mm]
\hline
\textgt{ロシア式記号} & \left( b/a \right) 1 & \left( b/a \right) :2 & \left( b:a \right) :m & \left( b:a \right) \tilde{b} & \left( a/a \right) /m & \left( b:a \right) :2m & \left( b:a \right) :m:\tilde{a} & \left( b:a \right) :\tilde{b}:\tilde{a} & \left( a/a \right) :2m \\[0mm]
\hline
& & & & & \left( c/b:a \right) :m & & \left( b:a \right) :2\tilde{a} & \left( b:a \right) :2 \odot \tilde{a} & \left( c/b:a \right) :2m \\[0mm]
\hline
\textgt{対称要素} & \begin{minipage}[b][95pt]{130pt}
\includegraphics[width=130pt,height=95pt]{tex17tplaneable_001.bmp}
\end{minipage}
& \begin{minipage}[b][86pt]{121pt}
\includegraphics[width=121pt,height=86pt]{tex17tplaneable_002.bmp}
\end{minipage}
& \begin{minipage}[b][85pt]{93pt}
\includegraphics[width=93pt,height=85pt]{tex17tplaneable_003.bmp}
\end{minipage}
& \begin{minipage}[b][86pt]{97pt}
\includegraphics[width=97pt,height=86pt]{tex17tplaneable_004.bmp}
\end{minipage}
& \begin{minipage}[b][80pt]{97pt}
\includegraphics[width=97pt,height=80pt]{tex17tplaneable_005.bmp}
\end{minipage}
& \begin{minipage}[b][88pt]{103pt}
\includegraphics[width=103pt,height=88pt]{tex17tplaneable_006.bmp}
\end{minipage}
& \begin{minipage}[b][112pt]{141pt}
\includegraphics[width=141pt,height=112pt]{tex17tplaneable_007.bmp}
\end{minipage}
& \begin{minipage}[b][113pt]{132pt}
\includegraphics[width=132pt,height=113pt]{tex17tplaneable_008.bmp}
\end{minipage}
& \begin{minipage}[b][113pt]{131pt}
\includegraphics[width=131pt,height=113pt]{tex17tplaneable_009.bmp}
\end{minipage}
\\[0mm]
\hline
\end{array}
\ \\
\ \\
\begin{array}{|c|c|c|c|c|c|c|c|c|}
\hline
\textgt{国際記号} & p4 & p4mm & p4gm & p3 & p3m1 & p31m & p6 & p6mm \\[0mm]
\hline
\textgt{ロシア式記号} & \left( a:a \right) :4 & \left( a:a \right) :4m & \left( a:a \right) :4 \odot \tilde{a} & \left( a/a \right) :3 & \left( a/a \right) :m & \left( a/a \right) m & \left( a/a \right) :6 & \left( a/a \right) :m \\[0mm]
\hline
& & & & & & & & \\[0mm]
\hline
\textgt{対称要素} & \begin{minipage}[b][116pt]{121pt}
\includegraphics[width=121pt,height=116pt]{tex17tplaneable_010.bmp}
\end{minipage}
& \begin{minipage}[b][116pt]{115pt}
\includegraphics[width=115pt,height=116pt]{tex17tplaneable_011.bmp}
\end{minipage}
& \begin{minipage}[b][114pt]{119pt}
\includegraphics[width=119pt,height=114pt]{tex17tplaneable_012.bmp}
\end{minipage}
& \begin{minipage}[b][109pt]{147pt}
\includegraphics[width=147pt,height=109pt]{tex17tplaneable_013.bmp}
\end{minipage}
& \begin{minipage}[b][98pt]{145pt}
\includegraphics[width=145pt,height=98pt]{tex17tplaneable_014.bmp}
\end{minipage}
& \begin{minipage}[b][99pt]{143pt}
\includegraphics[width=143pt,height=99pt]{tex17tplaneable_015.bmp}
\end{minipage}
& \begin{minipage}[b][98pt]{145pt}
\includegraphics[width=145pt,height=98pt]{tex17tplaneable_016.bmp}
\end{minipage}
& \begin{minipage}[b][98pt]{147pt}
\includegraphics[width=147pt,height=98pt]{tex17tplaneable_017.bmp}
\end{minipage}
\\[0mm]
\hline
\end{array}

壁紙模様の対称性の第13番目の類は，対称性3の図形を，60°で交差する２つの等価な並進軸$$(a/a)$$で並進して得られる．

国際記号で$$p3$$，ロシア式記号で$$(a/a):3$$です．今回から始まる残り５つの対称性の類（第13~17）は，正3角形のメッシュに属します．

等価な図形が隙間なく平面を充填しているこの対称性のパターンを以下に示します．モチーフ（非対称要素）は，正3角形メッシュ座標を作っている頂点に集まる曲線で囲まれた形です．

非対称要素（モチーフ）３つで，単位胞の面積に等しくなります．鏡映対称はありません．

以下の例は，アルハンブラの有名なモザイクです．これは対称性$$p3$$の例です．ただし，色の区別はしていません．

（参考）以下の「千鳥」のパターンの対称性は$$p3$$ではありません．何故でしょうか？

（解答）上図の「ちどり」のパターンは，単位胞の菱形の頂点に6回軸がありますので，$$p3$$ではありません．このパターンは，後ででてくる$$p6$$の対称性です．単位胞の中を，2つの千鳥図形で埋まますが，この千鳥の形は，等価なモチーフにさらに3分割できますから，非対称要素は，千鳥を3分割したものになります．

■第14の類は，国際記号で$$p3m1$$，ロシア式記号で$$(a/a)：m･3$$と記述します．対称性$$3･m$$の図形を60°で交差する等価な２つの軸$$(a/a)$$に沿って並進させて得られますが，鏡映面（赤色）の入り方が，並進軸（青色）に直交している．

非対称要素（黄色）が6個で単位胞を埋める．

■第15の類は，国際記号で$$p31m$$，ロシア式記号で$$(a/a)･m･3$$と記述します．並進の格子$$(a/a)$$は同じですが，鏡映面の入り方が，並進軸方向に平行である．

上の図で鏡映面は格子に重なっている．非対称要素（黄色）が６つで単位胞を埋めている．

■この両者の区別は多くの書物で混乱がみられます．分かりにくいので，もう少し詳しく説明を加えましょう：

美しい幾何学，p.100，p.110より引用

■第16の類は国際記号で$$p6$$，ロシア式記号で$$(a/a):6$$です．

以下のペルシャのパターン（Owen Jones）の例では，黒い6角形の内の花は厳密には6回対称ではありませんが，これを6回対称とみなすと，周りに風車がまわっているような6回軸の配列のパターンが見えます．

6回回転軸が通る点を頂点とする平行4辺形が単位胞．非対称要素モチーフが6個で単位胞を埋めます．

 エッシャー作品の例

■第17の類は国際記号で$$p6mm$$，ロシア式記号で$$(a/a)･m･6$$，あるいは$$(a･a):m･6$$です．

$$p6$$の対称性に鏡映面が加わりますが，並進軸に平行な鏡映面も，垂直な鏡映面もあります．

非対称要素である直角3角形が12個で単位胞を埋めます．

 対称性の法則をもっと利用すると，アーティストがデザインパターンのモチーフを変形するのが容易になる．

17種類の平面群の対称要素のマップとパターンを一覧にまとめます．

■17種類の平面群の対称要素のマップ

■17種類の平面群の非対称モチーフのパターン

人間は様々な用途で無限に繰り返す平面パターンを使います：壁紙，寄せ木細工，タイルの床，瓦屋根，陶器や装飾石の壁，レンガや敷石，道路や広場の舗装，色織物，カーペットや編物，同一物の密な充填，金属やプラスチック板から標準物を大量に打ち抜く，その他の多くの分野で利用されます．

自然界の網目パターンは，魚の鱗，生体組織の細胞，ハチの巣，マツカサの鱗片，などの配列で見られます．特に興味深いのは，結晶中の，原子・イオン・分子が配列した網平面です．もちろん，これらを直接見ることはできませんが，X線や電子線の回折や，走査型顕微鏡を用いて観測できます．
網目パターンから受ける印象を分析すると，芸術家が特定の視覚効果を伝えるために，特定の対称性クラスを意識的に選択する法則を確立できるかも知れません．

例えば，斜交する並進軸を持ち，対称面を持たないパターン（図112）は，斜め方向の動きを強調したい場合に適しています．

階段，ロビー，エスカレーター，地下鉄の傾斜トンネル，アーチ橋のフェンスなどの壁を飾る際に，芸術家はこの問題に遭遇します．

図117　　　　　　　　　　　　　　　　　　図121　　　　　　　　　　　　　　　　　　図123

水方向の並進軸はあるが，垂直方向の対称面を持たないパターン（図115，117参照）は，特定方向として水平面に沿った動きを強調しているので，地下鉄や回廊の水平通路の装飾に用いると成功します．対称面があると，それらに垂直な方向への運動を止めます．例えば，図121,123などのパターンは，水平方向には静止しているように見えます．図121では，２回軸が存在することで，上下方向への運動の概念が生まれますが，図123では，それらの回転軸が存在しないので，上方向，あるいは一般的に，垂直な一方向の運動の印象を与えています．
図121は，回廊の水平な床や天井の装飾にふさわしく，図123は， 地下鉄の昇降路の床や天井の装飾に適しています．

　図128　　　　　　　　　　　図130　　　　　　　　　　　図137　　　　　　　　　　　図147

水平や垂直の対称面のシステム（図128,130,137,147）がいくつか存在することで，静止休息，記念碑性，不動性，重力などの印象を醸し出します．興味深いことですが，(b:a):2･m型の対称パターン（図128 と 130）は，長い間，壁紙に使用されてきました．そして，図137や147に示すようなさらに対称的なパターンは，寄せ木，天井，ステンドグラス窓などには使われました．
奇妙な静止のない印象は，主要部分に映進面がある対称パターン（図116と120）で生み出されます．言葉でうまく表現できないのですが，これらのパターンの中の図形が，押し合い，転がり，絡み合い，群がって動きがあります．

　　　　　　　　　　　図116　　　　　　　　　　　　　　　　　　　　図120

このタイプの対称性は，他の対称性よりも出会う頻度は少ないのですが，それは，他のものよりも構成や認識が困難であるためで，例えば，見本市会場や遊歩道などのデザインに利用されることがあります．

　　　図132　　　　　　　　　　　　図139　　　　　　　　　　　　　　図145

特に興味を惹くのは，対称面がなく，3,4,6回回転対称軸で特徴づけられるパターン（図132,139,145）です．このようなパターンは，そのダイナミックさから，ダンスホールなどの大勢の人が無秩序に動くことを想定した施設の床や天井に適しています．図116のようなパターンと合わせて，文化公園の広場やサーカスのテントのアリーナ，フローティング・パネルなどの装飾に使用されています．全体として静止休息の奇妙な印象と細部に見られる動きは，普通の対称面と映進面が交互に繰り返すパターンのせいで生じています（図12,135,142）．静止休息と運動の印象のどちらが支配的になるかは，フレーム・ワーク（垂直，水平線に）に対するパターンの方位に大きく依存します．

　　　図135　　　　　　　　　　　　図142

例えば，図12はこの本に掲載している向きでは，動きの印象が静止に打ち勝ってしまう．特別な注意を払わずにパターンを見ると，対称面を見落とすのです．
一方，図12と同じ対称性を持つ図135は，動きよりも静止の印象が打ち勝ってしまう．それは，本を普通に置いたときに，パターンの対称面は垂直・水平線に沿ったフレームに平行であるからです．
観客が網目パターンを見たとき生じる印象に対称性が演じる役割について詳しく述べてきました．明らかに，対称性が美的鑑賞の唯一の要因ではありませんが，パターン構築の基礎となる法則を明らかにすると，装飾美術で対称性の果たす役割は，デッサンで遠近法が果たす役割と同じです．

■最後に，私が気に入っている映進面のある軽快な歩道タイル張りの写真を掲載します．美しい幾何学（技術評論社）p.93より