日本の数学月間

大変暑い夏でした．皆様お疲れのことと思います．どうぞご自愛ください．
2020年の数学月間（第16回）は，新型コロナウイルス感染拡大のため，
例年のような集会は困難と思われたので，ZOOMによるリモート実施の方針を固め，
準備の一環としてyoutubeチャンネル「NPO法人数学月間の会」を3月末に開設しました．
4月初めには，昨年度実施の講演ビデオはすべてこのチャンネルにアップロードを終えました．
今年度の講演ビデオもこのチャンネルにアップし，会員外にもすべて無料で公開しています．
今後このyoutubeチャンネルの充実をはかって参りますので，皆様，育成のご協力お願いいたします．

■さて，2020年の数学月間は7/22～8/22の間にZOOMのメリットを活かして分散型で実施しました．
ZOOMのメリットとは，時間と場所の制約がないことです．講演者も参加者も遠方からでも参加でき
日時も自由がきくので，４件の講演を数学月間の期間内に分散して行いました．
講演時間それぞれ2時間に延び十分にとることができました．
欠点は，参加者がインターネットとZOOMをやる方に限られることですが，これはや無負えないことです．
これを補うために，すべての講演ビデオをyoutubeブランドチャンネルに公開しました．
数学月間の1月間に実施した講演は以下の通りです：
7/22，宇宙エレベータ，八坂哲雄，
7/23，同志社中学校の数学博物館，園田毅，
7/29，感染症の数理モデル，稲葉寿，
8/22，X線・中性子で見る表面・界面，桜井健次
種々の話題があり，なじみのない分野の方々にも伝わるように
平易な解説記事をホームページに掲載しますのでご覧ください．

■月間最終日の8月22日,17:00～17:20に，
学術会議，数学教育分科会委員長の真島秀行先生より，追加プレゼンがありました．

この緊急提言の趣旨は，統計の教育カリキュラムの実効性を高めることにあります．
高校カリキュラムには，数列，ベクトル，統計が含まれており，
統計学はセンター試験に出題されるのだが，選択者は少ない．
たまたま，新型コロナのニュースで統計データが国民の目に入る昨今の状況を見ると
統計教育への関心を高める良い時期である．
令和4年から始まる新学習要領で統計学をきちんと教育するには，
教える側の先生への講習等の準備を始める必要がある．

■数学を体験，数学祭り

多くの人々が数学に関心をもつようになるイベントを数学月間では応援しています．講演会，講習会，ワークショップ，様々な活動形態がありますが，子供たちが楽しめて数学感覚が身に着く”数学まつり（フェスティバル）”は，英国のMMPでも米国のMAMでも，とっとりサイエンスワールドでも大変人気があります．学校カリキュラムの補完ではなく，数学力を伸ばす地域の数学サークル活動，学校の昼休にみんなが参加できる数学ゲームなどが，米国の学校で効果を上げています．

国立数学博物館MoMath(National Museum of Maths)は，米国唯一の数学博物館で，ニューヨークのマディソン・スクエアに，2012年12月15日オープンしました．ここには30以上の対話型の展示があります．東京でもMoMathのような常設の数学展示のあるものは，科学技術館，リスーピア，東京理科大「数学体験館」(2013年オープン）などあります．

 ■同志社中学校数学博物館Do★Mathは，2016年6月にオープンしました．キャンバス移転の2010年に，全教科が専門教室をもつ方式が採用され，数学科も6つの教室（数学１，2，3それぞれ専用の教室がある），メディアスペース（博物館として展示）があります．博物館には，「見る読むゾーン」，「触れる体験ゾーン」などがあり，特に，触れる体験というのは，この時期最も貴重だと思います．ピタゴラスの定理，$$Σn^2，Σn^3$$，正4面体の2分割，ソーマキューブ［体積$$3×3×3$$のキューブを7つのパーツ（体積4のパーツ6個と体積3のパーツ１個)で組み立てる］などの手で触れ体験できるパズル，誕生日当てゲーム［2進数の利用］，ハノイの塔などさまざまあります．展示物は，教職員が製作したものや，生徒が自由研究で製作したものもあります．写真のシェルピンスキーのフラクタル模型は，授業で生徒たちが牛乳パックを用いて１辺14cmの正4面体を１つづつ製作したものを合体させて作りました．

米国のMoMathや，数学サークル活動を思わせるこのような意欲的な活動が，単独の学校の教育の場で実現しました．ここは，授業で使用しますが，生徒が昼休みなどに親しむこともできます．さらに一般市民の見学も受け付けています．手で触り自分で体験することは数学や科学への出発点になります．

数学月間懇話会（2020.7.24）はzoomで実施され，Do★Mathを園田毅先生（同志社中）にご案内いただきました．

皆様，新年おめでとうございます．今年もよろしくお願いいたします．
covid19の感染拡大が続いています．お気をつけてお過ごしください．
数学月間のイベントもしばらくの間ZOOMでのリモートになります．
今日は，12月26日に実施した数学月間企画講演（第3回）
3Dジグソーパズルのデザインと数理，手嶋吉法（千葉工大）
の講演日ビデオのご紹介です．
https://youtu.be/j30dSZVAC1U
他の数学月間youtubeビデオへのリンクは，数学月間の会のホームページ
http://sgk2005.saloon.jpにありますので，こちらもご利用ください．

２Dジグソーパズルは，皆様やったことがおありでしょう．4角形のピースの形は，やはり２Dのジグソーパズルです．
３Dジグソーパズルは，内部も詰まっていますから，6面体の形のピースからできています．
表面やコーナーに収まるピースは周囲との連結数が少ないですが，一般の内部に収まるピースは6面体のそれぞれの面に連結の接手があります．そして，出来上がった3次元立体は，レイヤーごとにとり外せる構造なので，いくつかのタイプの同じ形のピースから構成されるようです．
ビデオを見てどのようなタイプのピースに分類できるか考えましょう．３Dジグソーパズルは，大工や指物で使う接手と同じ考え方です．箱根細工と似たところもあります．

数学月間企画講演の第3回は，12月26日(土)，15:00-17:00に，27名の参加で実施しました．
この1年間は直接の会合ができず，物足りなさの残る年度でした．とくに，インターネットをやらない会員各位にはご不便をおかけします．ここに年度後半の概要を報告いたしますのでご利用ください．なお，内容詳細は，NPO数学月間の会HPの記事，および，そこにあるリンクからyoutubeに公開した講演動画をご覧ください．
■企画講演（第3回）3Dジグソーパズルのデザインと数学，手嶋吉法（千葉工大）
３D ジグソーパズルとは立体ジグソーパズルのことですが，市販されている地球儀ジグソーなどは，球表面の地図ですので，２Dジグソーになり，３Dジグソーではありません．3Dジグソーパズルの起源は，2000年の池上裕司氏（理研，機械設計）の発明だそうです．講演者もこの直後に理研に在籍し池上氏とともに研究しました．現在も大学で研究テーマの一つとしておられるとのことです．今回の講演内容は，町屋佑季氏（修士論文）の研究に関わります．3Dジグソーパズルは，ピースが全部ばらばらに分解できるものでなければなりません．例えば，3×3×3 のジグソーパズルは，ばらならになる27個のピースよりなります．

３D ジグソーパズルのヒントは，日本の伝統的な継手（柱を繋ぐ技術）「四方継」にあります．池上式３D ジグソーパズルは「四方繋」を応用して作られました．ジグソーの仕組みをみると，「溝」と「ほぞ」は，常にかみ合っているわけですから，このかみ合わせ部分を1本のパイプで表現すると，ジグソーパズルの構造は空間のパイプの組み合わせとしてモデル化できます．

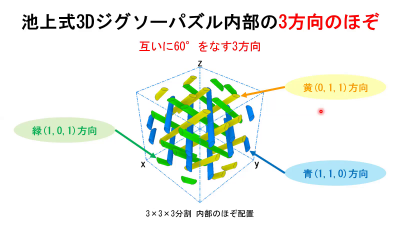
上図のような，無限に伸びたパイプの組み合わせで作られた周期的な構造は，その対称性を空間群で記述できます．この構造例では，空間群は$$Im\bar{3}m$$ で，ジグソー立方体の点群は $$m\bar{3}m$$であろうと推察されます．

町屋佑季氏は，作った3×3×3，4×4×4，5×5×5などの各３Dジグソーパズルを分解し，それぞれを構成するピースの形の種類と個数を分類し報告しています．これらの結果を，立方体内のサイト・シンメトリーとその同価ピースの個数という視点で再検討すると，非常に興味深い知見が得られると思います．

■企画講演（第４回）「虹の数学」を高校・大学で講義して，真島秀行（お茶の水女子大名誉教授）

講演者は，2002年から，高大連携プロジェクト，教養基礎の一環として，「虹の数学」を，附属高校１，２年生に開設しました．これは物理と数学の授業と連携して実施され，種々の現象の理解に数学が関わっていることを体験させることが狙いです．虹シート（ビーズ）などの教材があり虹の実験も行えるとのことです．

講演内容の詳細は，数学月間HPにリンクがありますので，youtube動画や資料pdfをご覧ください．ここに掲載する短い記事が，物理の視点から現象の理解を深め，数学へのガイドとなれば幸いです．

■幾何光学の視点

虹の現象は，幾何光学による理解と，波動光学による理解とがあります．まず，幾何光学による基礎的な知識から理解できることは，主虹の外側に副虹（主虹より遥かに暗い）が見えることの説明です．筆者が作成した模式図をご覧ください．これで，主虹と副虹が生じる原理がわかるでしょう．

太陽からの光は散乱角$$180°-φ$$の方向に散乱されて目に届きます（$$φ$$ は散乱角の補角）．

雨滴内部で１回反射して見える主虹の場合は，$$180°-φ=160°-6β+2α$$，2回反射して見える副虹の場合は，$$180°-φ=360°-6β+2α$$ で，屈折の法則，$$sinα/sinβ＝n$$（水の屈折率は，可視光域で，$$n=4/3$$に近い）を用いて計算すると，主虹と副虹の場合，それぞれ，角度$$φ=42°，φ=51°$$  が得られます．しかし，目に届く光線はキッチリ角度$$φ$$ だけに来るわけではありません．太陽からは平行光線が雨滴に入射しますが，雨滴の球表面の曲率のため入射点で入射角 $$α$$は変化します．そのため光線の屈折経路は図示した1本ではなくそのまわりに拡がります．光線の集まる「焦点」は非点収差のために「火面」と呼ばれる拡張された概念になり，火面の形は光線束の包絡面になります．幾何光学での説明はここまでです．幾何光学だけでは，主虹と副虹で色の配列順番が逆転することは言えても，波長による屈折率の変化（光の分散）を語るには，波動論の概念が必要です．

■波動光学の視点

波長と分散，位相と干渉などの現象は，本来，光の波動論で導入できる概念です．可視光の波長は，雨滴直径の1/1000程度になります．

雨滴球内を進む波面の形状は，ホイヘンスの原理から説明でき，火面の各点を波源とし生ずる球面波を，位相のずれを考慮し重畳して得られる同位相の波面フロントです．この波面フロントを位相面内の変位 （光線方向に垂直）の3次関数で記述したのがエアリーの功績です．雨滴から観測者までの距離は非常に大きいため，雨滴の波面フロント各点を波源とする球面波は観測位置ではほとんど平面波の重畳となります．この電場を表す式が次に示すエアリー積分です：$$A(\theta )=\displaystyle \int_{0}^{ \infty }\textrm{cos}\displaystyle \frac{\pi }{2}\left( x^{3}-\theta x \right) dx$$

．ここで， $$θ$$は光線に沿った視角の外れ量に比例した変数です．エアリー積分$$A(θ)$$ は光線電場の振幅ですので，$$θ$$ 方向に観測される虹の強度は $$|A(θ)|^2$$になります．小さい雨滴サイズが均一で，空気が奇麗で空気による吸収や散乱がないと，主虹のすぐ内側にかすかに色づいた過剰虹が観察できることがあります．過剰虹は，このような光の干渉の効果で生じるものです．

エアリー積分の数値計算は，被積分関数を級数に展開したもので行なわれましたが，収束が悪いためになかなか困難でした．

後に，ストークスはエアリー積分が解となる微分方程式の解の漸近挙動を研究しました．この近似手法は，量子力学のWKB解でも用いられています．