ロシアの数学月間

約4000年前のバビロニア時代に三角形の幾何学の研究が始まりました．その後のエジプトでは，ナイルの氾濫後の測量に必要な幾何学が発展しました．3,4,5の長さのエジプト紐で直角を作り，ピタゴラスの定理も知られました．ギリシャでユークリッドが原論を完成したのがB.C.300年頃です． 普通の学校の幾何学の教科書にあるほとんどすべての事実が，17世紀の半ばまでにすでに知られていました．ユークリッド幾何学の分野で，単純な定理は出尽くしたように見えますが，まだ発見が残されていたとは驚くべきことです．先に掲載した　ナポレオンの定理https://note.com/sgk2005/n/n9593e9c0cae6
は，1800年頃の発見です．
2000年に，オランダ人のvanLamunは次の驚くべき性質の円を発見しました．

上の図をご覧ください．緑の３角形の辺の中点を対向する頂点と結ぶ（青線分）．３つの青線分の交点は重心と言われます．始めの緑の３角形が，６つの３角形に分割されました．この６つ3角形の外接円（点線の円）の中心（６つあります）は，ある一つの円周上に乗ります．この円（赤い円）は，ヴァンラムン円と呼ばれます．手ごわそうです．皆様，証明をお考え下さい．

（グリゴリイ･フェリドマンの記事：Kvantik（2012）６，p.9を参考にした）

ユーリ・マルケロフ「kvantik」＃ 3、2019の図を引用しますが、設問は変更しました。

図：1

ポリオミノとは、何個かの正方形セルを側面に接合した形状です。たとえば、テトラミノは4つのセルのポリオミノであり、形状は5種類あります（図1）。5つのセルからなるポリオミノはペンタミノと呼ばれ、12種類の異なる形状があります（図2）。

Q1．図２には１つのペンタミノが抜け落ちていますが、どんな形が抜けているかわかりますか．

図：2

テトラミノのある１種類を選び、選択した種類のテトラミノのみを使用して、以下の図形を作成してください？（テトラミノは裏返すことができます。）
答えを図3に示します。

図：3
ペンタミノについても同じ質問をしましょう。ここでは状況が異なることがわかります。
ペンタミノのタイプを選択して、選択したタイプのペンタミノのみを使用して、作成できるような有限の図形はありません。
何故でしょう？

問題がわかりにくいので、この問題を私は次のような設問に変更します：
Q2．ある有限図形があって，１2種類あるペンタミノの任意の1種類を選択して，そのペンタミノのみでその形を分割できるとする．
そのような有限図形はありますが？

Q3．十字架（図4）だけ，あるいは，アーチ（図5）だけに「分割」できる有限の図形が存在しないことを証明してください。

図：4、　　　　　　図：5、　　　　　図：6

図：7
図7の例は、ある図形の4種類の分割例です。残りの8種類のペンタミノのうちの1種類を使ってこの有限図形の２分割はできません．

GeorgeSichermanが発明した図は、8種類のペンタミノに分けることができます。

ポリオミノや他の図に関する多くの興味深い問題や写真は、recmath.orgで見つけることができます。
アーティストArtyomKostyukevich

 
2019/20年度の数学コンクールの年間ツアーの問題から、幾何の問題をいくつか選びました。2019/2020年度の年間ツアーの応募は終了しました。受賞者は12月号で発表されます。この数学コンクールは5年生～8年生が対象です。なかなか難しい問題です。試しにご挑戦ください。

ラウンドXー問題50（ジョン・コンウェイ）
図に示すように、任意の三角形の各辺が両方向に延長して得られた6つの点は1つの円上にあることを証明しなさい。

ラウンドIXー問題43 （Mikhail Evdokimov）
図に示すように、 正三角形 AMB と ANCは、一辺の長さ１の正方形ABCDの対角線と側面に作成 されます。距離MNを求めなさい。

ラウンドVIIー問題32 （Mikhail Evdokimov）
正方形ABCDのBC側には、外側に正三角形BMCを描きます。線分ACとMDは点Oで交差します。OA = OMであることを証明しなさい。

ラウンドIVー問題18
図示されているように、点Kは、二等辺三角形BACの底辺BCを長さxとyに分割します。角度AKCが60°の場合のAKの長さを求めなさい。

ラウンドIー問題4 （Mikhail Evdokimov）
図に示すように、2つの正方形が平面上にあります。一方の正方形の中心がもう一方の正方形の対角線上にあることを証明しなさい。

 https://elementy.ru/nauchno-populyarnaya_biblioteka/435720/Pryamoe_na_krivom_ili_Progulki_po_iskrivlyonnoy_poverkhnosti

 ヴァレリア・シロタ「Kvantik」No.8，2020

まっすぐで平らな道なら、どこでも曲がらずにまっすぐ進むのは容易です。または、広い平原で、遠くにゴールやランドマークが見えればまっすぐ進めます。もし、途中に丘や渓谷があり、さらに、霧や、真っ暗だったりした場合はどうでしょう？どこにまっすぐ行くのか、どうすればわかるでしょう？曲がりくねった山道を歩いているときに「直線に沿って歩く」とは何でしょうか？そして、この坂道を振り向かずに進んでいくと、どこにたどり着くのでしょうか？

そのような疑問にも対応できるようにしていきたいと思います。まずは直線（普通の平面上）とは何かということから始めましょう。次の定義が一番良さそうです。

平面上の直線とは、その2つの点を結ぶ最短経路です。

（図１）直線上の任意の2点を取ります。 ある点から別の点に可能なすべての線を描きましょう。 直線上の線分は、これらすべての線の中で最も短いものになります．

この定義は、「まっすぐ進む」という指示に合います。ゴールが直線上にある場合は常に、これがその直線で最短経路です。確かに、ゴールがあなたの直線上にない場合、あなたはそれに到達することは決してありません...

（図２）破線

演習1.（図2）が直線ではないことを証明しなさい。

この演習から、私たちの定義では「どこでも曲がれない」ことがわかります。急に曲がると破線になり、これは最短経路ではありません。

演習2.科学者のシギムントは特定の線を研究し、それが直線であることを証明したいと考えています。彼はすでに、この線に沿った点Aから点Dへの 経路が最短であることを証明することができました 。点BとCがAとDの間のこの線上にある場合、この線に沿ったBからCへのパスも最短であることを証明しなさい。

演習3.科学者マクシミリアンは、点A、B、Cが乗っている別の線を調べ ます。彼は、この線に沿ったAからBへの経路が最短であり、BからCへの線に沿った経路も最短であることをすでに証明しています。これは、この線に沿ったAからCへのパスも最短であることを意味しますか、それともまだ証明すべきことがありますか？

平面上の直線はわかりました。では、この定義を曲面に当てはめてみましょう。例えば、非常に急峻で高い山があるとします（図3）。A地点からB地点までの最短経路は？　確かに山上を通るものではありません。最短の道は、図中の緑の線が示すように、明らかに山の麓のどこかを通っています。演習２で見たように、この線上のＡとＢの間にある点のペアについても、最短経路の条件が成り立つなら、これが直線でしょうか？　さらに、山が対称で、点Aと点Bが厳密に異なる辺にあるとすると、このような最短経路は2つあり、どっちも直線なのですね！？

（図 3）急峻な山。 点Aから点Bへの最短経路は何ですか？

大体そのような考えで良いのですが、しかし、1つの問題があります。ポイントAと Bを超えてこれらの「直線」の延長を正しく描画する方法は？　これらの延長は平坦な地形で実行され、すでに「実際の」直線の線分のように見えます。ただし、「直線」に切れ目があってはならないことを覚えています（演習1を参照）。切れ目付近では、「最短経路」条件に違反します。したがって、Aと Bを通過する緑色の「直線」の「端」は、空間内の点Aと Bを通過する直線の非常に先の遠方です （これは、説明した表面上にはありません！）。

そして、ここで問題が発生します：山の周りから遠ざかれば、直線が山の周りをまわる必要はありません。 図3の点Kから点Nまでの最短経路は別の直線になります。

さて、直線の定義は間違っていましたか？それとも、山岳地帯に拡張することは不可能ですか？いいえ、それほどひどい違いではありません：少し修正が必要なだけです。結局のところ、どんな曲面でも、その小さな部分を見ればすべてが小さな平面と見なせます。

「すべてをまっすぐに、まっすぐに」するには、遠くのゴールではなく、一歩先のゴールを見続けなければなりません。そうすれば、表面の曲率には気づかず、次の一歩を前の一歩と同じ方向に踏み出すことになります。そして、あなたが通った道の一つ一つの小片がまっすぐになります。結局のところ、そのすべての小さな部分の曲面は平面のように見えます。

したがって、曲面の場合の直線の定義では、2つの単語を追加します。直線に沿ったパスは、2つの十分に近い点に対して最短である必要があります。これですべてが整いました。この例の点KとNのペアは、十分に接近していないため、考慮できなくなりました。

これらの曲線を直線と呼ぶのは何か気が咎めるので、測地線という呼び方があります。これは、直線の概念を曲面の場合に一般化したものです。

曲面上の測地線は、その十分に小さい部分が、この曲面上の両端間で最短経路になるような線です。

それほど厳密ではありませんが、測地線は、すべての小さな（ほぼ平坦な）部分上で直線のように見える曲線です。

ちなみに、対称的な山の例では、描画した2つの測地線に加えて、第３の測地線が点Aと Bを通過し ます。これは、最初に最短ではないと拒否した山の頂上を通るパスです。これで、点AとBが十分に接近していないと宣言できます。

ご覧のとおり、ユークリッドの公理は、任意の2点（平面）を通る直線を1本だけ引くことができるというものですが、曲面の測地線ではまったく機能しません。たぶん、AとBを通る「直線」はもっと引けるかもしれません。山の形によりますが。

また、図３の緑と青の線のように、現実には「まっすぐ」な道（すなわち測地線）が、地図上では「曲がっている」ように見えることもあることを覚えておくと便利です。

***

これで、どような地形でも「まっすぐ進み、曲がらない」とはどういう意味かがわかりました。これは測地線に沿った動きです。今、どんな表面に対しても、次の質問をすることができます：

１．その測地線はどのように見えますか？
２．２つの与えられた点を通る測地線を描くには？
一般的な場合、この問題は難しいので、円柱と円錐という単純な「ほぼ平坦な」表面を歩くことを提案します。

シリンダー

図４： シリンダー

シリンダーを作るのは簡単です（図4）：紙を1枚取り、それを筒に巻き、端を接着します（できれば長辺に沿って）。カブトムシをその上に乗せて、それが這うように測地線を描くことができます。

最初から接着線に平行な方向を選択すると、カブトムシはこの線（および円柱の軸）に平行な直線に沿って這うようになります。このようなラインはジェネレーターと呼ばれます。軸に垂直な方向に移動を開始すると、測地線は円になります。

チャレンジ問題　斜めなど、他の方向に進むと、どのような線が表示されますか？

円錐

図5　円錐

すぐ作れます。接着も簡単です。最も簡単な方法は、大きな紙を取り、その側面の1つの点を選択し、この点で区切られた側面の2つの半分を接着することです（図5）。円錐の底面が不均一で、角が突き出ていても問題はありません。実際の円錐面は無限であり、これはほんの一部であると見なすことができます。

問題　この表面で測地線はどのように見えますか？

－－－続く

図28 左は球状の生地、右はベーグルの生地。パン屋さんは、左の生地を取り、細長い円柱になるように巻き、（トポロジーでは、充填された円柱は充填された球と区別がつかない）曲げて、この円柱の端をつなぎました。そうして球がベーグルになってしまった...。止まれ、接着は不可（許されません）!　 オブジェクトの種類が変更されます。

----------
私たちは、球の表面を取って曲げ、しわを寄せ、伸ばしてみましょう、どこも破らず、2つの点を1つに接着してはいけません。このようにして、例えば立方体を作ることができます。その方法を理解するために、ゴムでできた円から正方形を得る方法を示すなら、正方形の形を取るまで、円の境界の4つの点を外側に引っ張る。具体的には、円の境界の点が、正方形の外周の点に変わります。

縮めたサッカーボールのゴム表面を使って、いろいろなものを作ることができます。しかし、トポロジーが許す広い可能性の中でも、車の形表面を作るのは直感的に難しいと思います。球、楕円体、リンゴ、スイカ は作れますが、引き裂くか、いくつかの点を一緒に接着しないと、球からベーグルを作ることはできません。以上によれば、次の２つのタスクは区別する必要があります。1)膨らんだ風船から膨らんだベーグルを作る、2) 風船の表面からベーグルの表面を作る。第１の問題は、図28のキャプションで「解決」されています。

そしてオイラーは、この記述が証明できるかどうかに疑問を持った。直感的には全く問題ないのですが、数学は明白なことを厳密に証明された言語に翻訳するという問題を抱えています。結局のところ、例えば平面上に住む文明を発見したとしても、問題の事実はその住人には明らかではない（挿話２を参照）。そして、数学の力を借りて、定理の内容を伝えることができるようになります。
---------
（挿話２）アインシュタインのトポロジー
かつてA.アインシュタインは、彼の発見の本質は何かを誰にでもわかりやすい言葉で、非常に簡潔に説明するように求められました。彼は答えた：私たちは皆、目隠しされた小さな虫のように、大きな球の表面を這っています。私は、自分の住んでいる世界が曲がっていることに初めて気がつきました。しかし、具体的にどのように湾曲しているのか(空間のトポロジカルなタイプが何であるか)はまだよくわかっていません。
ーーーー

そして、ここからが本題です。数年前に数学者のG.ペレルマンが同様の事実を立証しましたが、大次元空間でのみです。局所的に湾曲した3次元空間に似ている多次元空間の図形についての事実。私たちは3次元空間に住んでいて、4次元を見たり感じたりすることはできません。第4次元が時間であることを推論することしかできないが、目では把握できない。だから、大次元空間の球体からトーラスを作ることは不可能だと冷静に納得することはできません。(結局のところ、4次元空間では、上述のように、トポロジーのルールを守りながら、左側に心臓のある人を右側に心臓のある人に変えることは可能である)

それを証明できる言語が必要です。そして、ペレルマンが「ポアンカレ仮説」を証明するまでに何年もかかった（証明された後は、ポアンカレ仮説やポアンカレ-ペレルマンではなく、ペレルマン定理と呼ばれるようになった）。オイラーが始めた分野は大きくなった。彼は、皆が明白だと思うことを正確で鉄壁の数学的推論に翻訳しました。球、スイカ、地球、湾曲した多面体、どんな丸いものでも表面に何かしらの地図を描いた（図２９）。

トポロジーの観点から言えば、どんな多面体も球体である。４面体は球体、立方体は球体、８面体、どんな平行６面体もすべて球体です。例えば、ゴムで作って膨らませばサッカーボール、つまり球体になる。オイラーの仕事以前には、トポロジーそのものが存在しませんでした。

オイラーは、これらの物体がすべて同じであると直感した。具体的にはどのような形でどう説明するのか？彼は、球体の表面とベーグルの表面とプレッツェルの表面が同じではないことをどうやって証明するかという問題に特に興味を持っていた。 

最初の質問に対する答えは、後にアンリ・ポアンカレによって明らかにされた（オーギュスト・コーシーが「連続関数」とは何かを明確にした後）。
オイラーはすぐに第2の問題（2つの面の非一様性の証明について）に目を向け、これを見事に解いた。

ーーーーーーーーーー

オイラー標数：（頂点の数）-（辺の数）+（面の数）

球体上に描いた地図とトーラス（ベーグル表面）に描いた地図で、オイラー標数を数えると違いがあり，この特性はトポロジー的な連続変形で変化するはずはないのだから，トポロジー的に違うものでなければなりません．
オイラー標数は：２（球表面），０（トーラス）

トーラス上の左の図形は

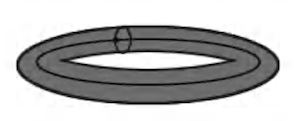
頂点の数１，辺の数２，面の数１