ロシアの数学月間

 
2019/20年度の数学コンクールの年間ツアーの問題から、幾何の問題をいくつか選びました。2019/2020年度の年間ツアーの応募は終了しました。受賞者は12月号で発表されます。この数学コンクールは5年生～8年生が対象です。なかなか難しい問題です。試しにご挑戦ください。

ラウンドXー問題50（ジョン・コンウェイ）
図に示すように、任意の三角形の各辺が両方向に延長して得られた6つの点は1つの円上にあることを証明しなさい。

ラウンドIXー問題43 （Mikhail Evdokimov）
図に示すように、 正三角形 AMB と ANCは、一辺の長さ１の正方形ABCDの対角線と側面に作成 されます。距離MNを求めなさい。

ラウンドVIIー問題32 （Mikhail Evdokimov）
正方形ABCDのBC側には、外側に正三角形BMCを描きます。線分ACとMDは点Oで交差します。OA = OMであることを証明しなさい。

ラウンドIVー問題18
図示されているように、点Kは、二等辺三角形BACの底辺BCを長さxとyに分割します。角度AKCが60°の場合のAKの長さを求めなさい。

ラウンドIー問題4 （Mikhail Evdokimov）
図に示すように、2つの正方形が平面上にあります。一方の正方形の中心がもう一方の正方形の対角線上にあることを証明しなさい。

ユーリ・マルケロフ「kvantik」＃ 3、2019の図を引用しますが、設問は変更しました。

図：1

ポリオミノとは、何個かの正方形セルを側面に接合した形状です。たとえば、テトラミノは4つのセルのポリオミノであり、形状は5種類あります（図1）。5つのセルからなるポリオミノはペンタミノと呼ばれ、12種類の異なる形状があります（図2）。

Q1．図２には１つのペンタミノが抜け落ちていますが、どんな形が抜けているかわかりますか．

図：2

テトラミノのある１種類を選び、選択した種類のテトラミノのみを使用して、以下の図形を作成してください？（テトラミノは裏返すことができます。）
答えを図3に示します。

図：3
ペンタミノについても同じ質問をしましょう。ここでは状況が異なることがわかります。
ペンタミノのタイプを選択して、選択したタイプのペンタミノのみを使用して、作成できるような有限の図形はありません。
何故でしょう？

問題がわかりにくいので、この問題を私は次のような設問に変更します：
Q2．ある有限図形があって，１2種類あるペンタミノの任意の1種類を選択して，そのペンタミノのみでその形を分割できるとする．
そのような有限図形はありますが？

Q3．十字架（図4）だけ，あるいは，アーチ（図5）だけに「分割」できる有限の図形が存在しないことを証明してください。

図：4、　　　　　　図：5、　　　　　図：6

図：7
図7の例は、ある図形の4種類の分割例です。残りの8種類のペンタミノのうちの1種類を使ってこの有限図形の２分割はできません．

GeorgeSichermanが発明した図は、8種類のペンタミノに分けることができます。

ポリオミノや他の図に関する多くの興味深い問題や写真は、recmath.orgで見つけることができます。
アーティストArtyomKostyukevich

約4000年前のバビロニア時代に三角形の幾何学の研究が始まりました．その後のエジプトでは，ナイルの氾濫後の測量に必要な幾何学が発展しました．3,4,5の長さのエジプト紐で直角を作り，ピタゴラスの定理も知られました．ギリシャでユークリッドが原論を完成したのがB.C.300年頃です． 普通の学校の幾何学の教科書にあるほとんどすべての事実が，17世紀の半ばまでにすでに知られていました．ユークリッド幾何学の分野で，単純な定理は出尽くしたように見えますが，まだ発見が残されていたとは驚くべきことです．先に掲載した　ナポレオンの定理https://note.com/sgk2005/n/n9593e9c0cae6
は，1800年頃の発見です．
2000年に，オランダ人のvanLamunは次の驚くべき性質の円を発見しました．

上の図をご覧ください．緑の３角形の辺の中点を対向する頂点と結ぶ（青線分）．３つの青線分の交点は重心と言われます．始めの緑の３角形が，６つの３角形に分割されました．この６つ3角形の外接円（点線の円）の中心（６つあります）は，ある一つの円周上に乗ります．この円（赤い円）は，ヴァンラムン円と呼ばれます．手ごわそうです．皆様，証明をお考え下さい．

（グリゴリイ･フェリドマンの記事：Kvantik（2012）６，p.9を参考にした）

18/19学年度のクバンチク数学コンテストなどの問題より
３つ選びました．挑戦してみましょう．

■雑誌エレメント2020.9より改題
平方数A_n（n=1,2,3,4,5,6････）とは；1,4,9,16,25,36，･････
（一辺nの正方形の中に直径１の円を並べたとき入る円の数）
3角数B_m（m=1,2,3,4,5,6,･･･）とは；1,3,6,10,15,21,･････
（一辺nの正3角形の中に直径１の円を並べたとき入る円の数）
平方数でもあり3角数でもある数を求めなさい．無限にありますがいくつ求められますか．
ヒント）A_n=n^2 ，B_m=m(m+1)/2　です．

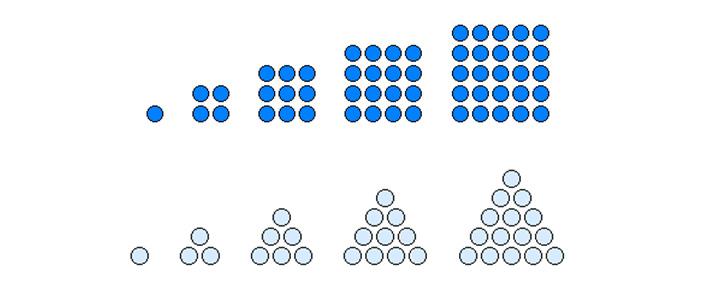
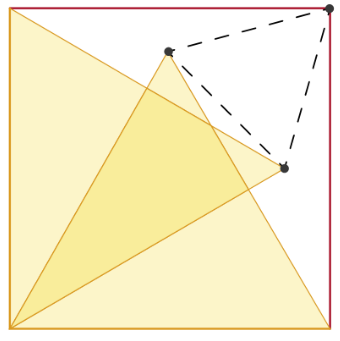
■７ラウンド問題34より
図に示すように，2つの黄色の等辺三角形が正方形に配置されています．マークされた3つのポイントが等辺の三角形を形成していることを証明しなさい．

■４ラウンド問題20（エゴールバカエフ）より
円は三角形の辺と6点で交差します（図を参照）．
a）a = bおよびc = dの場合，e = fであることを証明しなさい．
b）b = cおよびd = eの場合，f = aであることを証明しなさい．

改装後，すべてのランプを交換することにし，IQライトと呼ばれる新しいランプシェードを購入しました．重さはたったの100グラムです．30枚の薄いフレキシブル・プレートで組み立てられているので，とても軽い．各プレートは四角形の形状で，4つのフックがついています．このデザインは，デンマークのデザイナーHolgerStrömによって1973年に発明されました．名称のIQはInterlocking Quadrilateralsー連動する四辺形ーの略です．

図1を見ると，プレートが5個集まる場所と，3個集まる場所があることがわかります．
デザイン自体は一見複雑に見えますが，幸いなことに詳細な説明書が添付されており，組み立ての過程はわかります．
ランプシェードは同じ菱形面でできた多面体です（図2）．
その正確な学名はギリシャ語の数値接頭辞の表を見てください．例えば，30面体はロシア語ではТРИАКОНТАЭДРАとなります．

ヨハネス・ケプラー（1571-1630）

宇宙の調和（図3） でてくる，図の右側は30面体です．
30個の菱形面のうち10個しか表示されていませんが，菱形三十面体の名称が，テキストの2行目に認識されます．

図の左側は12面体です．

菱形の三十面体の発見におけるケプラーの優先順位を認めているようですが，菱形12面体と菱形30面体の菱形面の形についいて述べていないということです．

ヴェンツェル・ジャムニッツァー(1508 – 1585)

ドイツの有名な宝石商．1568年に、彼はPerspective Corporum Regulariumという本を出版しました。