Григорий Мерзон, «Квантик» №5, 2020 より
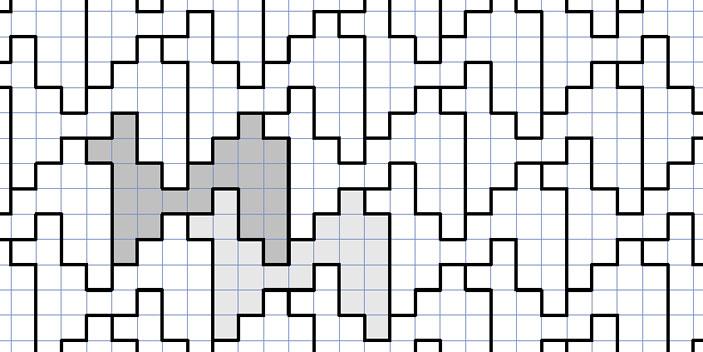
この記事の図には,不要なものもありましたので,必要なものだけ掲載します.文章は冗長ですので私が全部書き換えました.解が1つしかないような記述も私は気に入りません.要するに,この問題は,以下の図(ラクダと言っている)を3つの部分に直線で切り分けて,それらを組み合わせて正方形を作れという主旨です.パズルの問題として予備知識なしで考えるとなかなか難しいかもしれません.
この図(ラクダ)を見ると,うまく組み合わせれば,エッシャーの周期的な絵のように寄せ木細工が作れることに気づきます.それは下の図のようになります.ラクダのモチーフが周期的に繰り返されていることがわかります.
一つのラクダの頭に注目すると,右斜め上に次のラクダの頭があり,それらを結ぶ直線上に周期的に繰り返す頭が現れることがわかります.
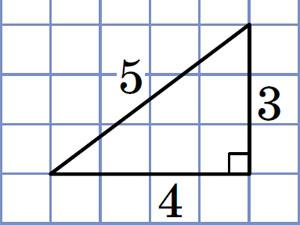
この周期はいくつかというと,3,4,5の直角3角形(この記事ではエジプト3角形と呼んでいる)にあてはめると,周期が5であることがわかります.
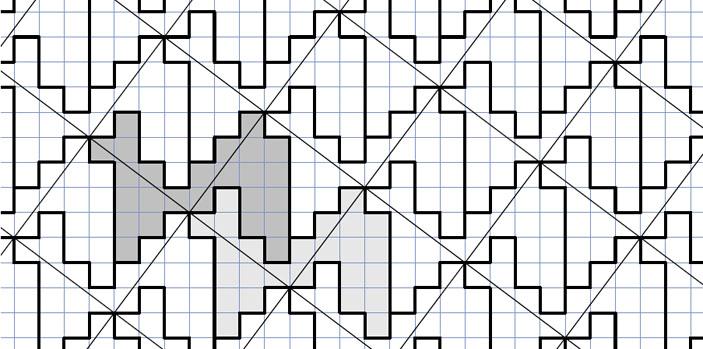
このエッシャーの周期的な絵(寄せ木細工)のような繰り返すラクダの壁紙は,斜めに置かれた1辺が5の正方形を周期にしています(私の説明流儀では単位胞と呼びます).
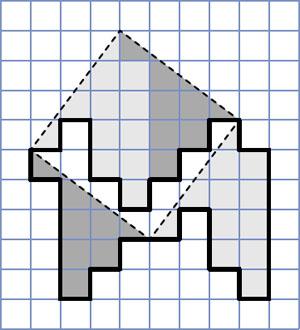
従って,以下のように3つの部分に直線で切れば,組み合わせて1辺5の正方形が作れます.
これがこの問題の答ですが,私は答えはこれだけではないことを指摘しておきたいです.
ラクダが3分割できる範囲にあるならば,単位胞の正方形はずらす(平行移動)ことが可能で,答えはこれだけではなくたくさんあります.
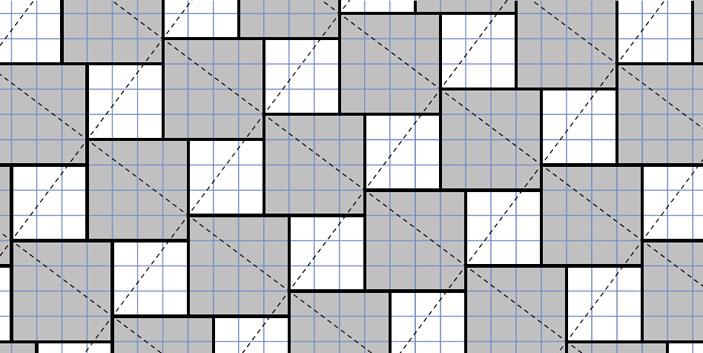
上の図は「ピタゴラスモザイク」といって,ピタゴラスの定理の証明になっています.これは9世紀にアラブの数学者アンナイリジとサビットイブンクラによって証明に使われたそうです.
アーティストAlexeyVayner