数学と基礎科学,谷,「数学文化」p.79-87,No15 (2010)より抜粋
以前の号に,現代の標準時計 を掲載しています.現代の標準時計は,水晶発振子と原子時計です.長さの標準は今日では「メートル原器」ではなく,真空中の光速で定義します.長さを光速で定義するには正確な時計が必要ですが,原子時計はそのような長さの定義に使用されています.GPSが位置を割り出すときにも正確な時計が活躍しています.
■今回の記事は,ガリレオの時代から始めます.
時間と空間の計測は最も基本的なものです.空間の測量は,紀元前に幾何学とともに発展しました.しかし,時間の計測は,地球の日周運動を利用した日時計,あるいは,水時計や砂時計から始まりました.その後,ロウソク時計,線香時計などが生活に現れ,やがて,歯車やゼンマイを用いた機械時計が作られるようになります.しかし,正確な時計は,18世紀の振り子時計まで待たねばなりませんでした.ガリレオ(イタリア,1564-1642)の”振り子の等時性”の発見は,エポックメーキングです.
正確な時計を持たなかったガリレオ以前の時代には,正確な観測に基づいた運動の研究は不可能だったわけです.
振り子を時計に取り入れたのは,ホイヘンス(オランダ,1656年)で,1675年には,ホイヘンスはヒゲゼンマイのついたテンプ時計も制作し,フランスで特許を取得しました[フック(英)も考案した(1664年)と主張します].これが,「世界初の実用的な機械式時計」の始まりです.
ガリレオの発見した”振り子の等時性”は,振り子の周期が,振り子の長さ$$l$$の平方根にのみ比例し,振幅や錘の重さにはよらないというものです.
周期は $$T=2\pi \sqrt{l/g }$$
と表せ,現在では$$g$$は重力の加速度で地球の場所により,わずかに異なることがわかっています.正確には,”振り子の等時性”は,振幅が小さいときに成り立つ線形近似です.振幅が大きくなると振り子の周期は長くなります.
$$T=2\pi \sqrt{\displaystyle \frac{l}{g } }\left( 1+\displaystyle \frac{1}{4}sin^{2}\left( \displaystyle \frac{\theta _{0 } }{2} \right) + \cdots \right) $$,ここで$$\theta _{0}$$は振幅の半分の角度.
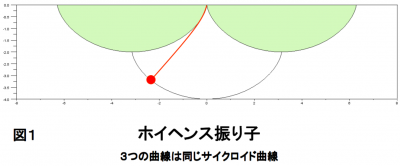
普通の振り子の軌道は円弧ですが,サイクロイド曲線に沿って動く振り子は,振幅が大きくても小さくても周期は不変です.ホイヘンスは,これを利用したサイクロイド振り子時計も作りました(図1).
ホイヘンスは,振り子時計の本と光の本を書き,微積分の先駆的研究もし,ニュートンと重なる時代を生きました.
その後の大航海時代には,海上で正確に経度を知ることが必要になりました.船の現在地(経度*)は,船の時刻と経度のわかっている地点の時刻の差から求めます.地球は24時間で一回転するから,1時間で経線15度の差です.*注)緯度は太陽の高度や北極星の高度からわかります.
1714年,イギリス議会は「経度を精度よく決定できる方法」に2万ポンドの懸賞を出しました.時計技師ジョン・ハリソン(英)は,30年近くも試作を繰り返し,苦心の4号機H4はポーツマスからジャマイカへの81日間の航海をすませた1762年1月19日に,時計から求めた経度と現地の天文観測から求めた経度との誤差が5秒という議会の要求(2分)をはるかに上回る成績を収めました.彼は,今日の懐中時計にも使われているグラスホッパー脱進機構を発明しています.
参考文献
http://www.nmm.ac.uk/harrison