■今回の記事は,2020年3月30日にマリアンヌによってプラスマガジンに提出されたエッセイの解説です.
How can maths fight a pandemic? By Marianne Freiberger ,https://plus.maths.org/content/
プラスマガジンの編集者,マリアンヌフライバーガーは,2020年3月24日にGogにインタビューしました.
エッセイの全文翻訳(by KT)は数学月間ホームページに掲載しておきます
これは大変長いエッセイで読み難いので,ここにレジメを作成しました.
このエッセイの書かれた3月30日ころは,Covid-19の感染について未知なことばかり(感染させるが症状の出ない保菌者など)だったでしょう.しかし,2.5か月経過した現時点では,これらは皆さんの常識になりましたね.最後に出てくる医療崩壊をさせないための断続的なロックダウン方法のシミュレーションは参考になるかもしれません.
■ケンブリッジ大学の疫学者ジュリア・ゴグGogは,2月の初めに,数理科学センターの通常の職務を辞し,緊急事態のための科学諮問グループ(SAGE)に結果を報告するモデリンググループ,SPI-Mに専念することになった.
SPI-Mは,インフルエンザパンデミックへ備えてこれまで活動をしてきたのだが,現在はCOVID-19のパンデミックに焦点を絞った活動をしている.ゴグは,王立協会が率いる全国コンソーシアムの運営委員会にも所属し,このパンデミックに対処している.
SPI-Mの仕事は,次に何が起こるか,さまざまな介入でそれがどのように変化するかを,予測できる数理モデルを開発し働かせることだ.COVID-19パンデミックがどのように進展するか?社会的介入はどのような影響を与えるか?これらのモデルはどのようなものか?それらは正しいのか?
COVID-19パンデミックの報道については、こちらをご覧ください:https://plus.maths.org/content/tags/covid-19
ーーーーーーーーーーーーーーーー
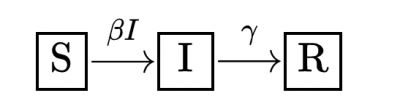
■SIRモデルとは(訳者補足)
S 感受性保持者数,(感染可能な数)
I 感染者数,(患者数)
R 免疫保持者数,(回復患者数)
全人口Nは一定と仮定して,N=S+I+R が成り立ちます.
SIRモデルの方程式は次のとおりです.
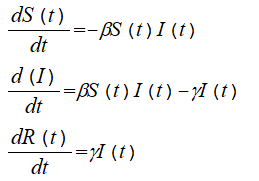
(1)(感染可能な数)の増加速度は,(患者数)と(感染可能な数)の積に比例する.比例定数βは感染率.
(2)(患者数)の増加速度は,(感染可能な数)の増加速度から,(回復患者数)の増加速度を減じたもの.
(3)(回復患者数)の増加速度は,(患者数)に比例する.比例定数γは回復率.
SIRモデルの詳細については,以下の記事https://plus.maths.org/content/mathematics-diseasesをご覧ください.
S, I, Rの間の状態遷移をブロック図で描くと上図のようです.
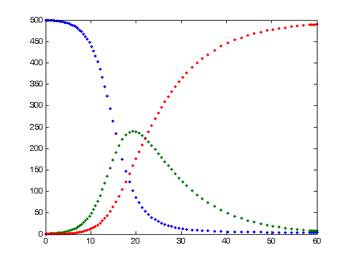
このモデル(単純SIR)で得られる結果は,下のグラフのようです.
S:青い線,I:緑の線,R:赤い線
赤い線は,「始めは免疫のあるものが誰もいなかったが,全員免疫ができて終わる」という当たり前の特別面白くない結果ではあります.
ーーーーーーーーーーーーーーーーーー
単純なSIRモデルは,寄宿学校の生徒などの単純な母集団に対して適切な予測を提供しますが,複雑な母集団に関しては,さまざまな母集団ごとのSIRモデルを繋ぎ合わせます.
実際には,これに色々な介入が加わるのですが,この影響を詳細にシミュレートするには,SIRモデルよりもさらに洗練されたモデルが必要です.
接触がカギ
このようなモデルの世界の背景で,非常に重要なのは人の接触パターンです(いわゆる動態調査):誰が誰にどのくらい会ったか.例えば,BBCとGogチームのコラボレーションとして2018年に実行された大規模な市民科学プロジェクトがあります.人々は,彼らの動きを追跡するアプリをダウンロードし,出会った人々(すべて適切に匿名化されている)を追跡するように求められます.モデルに組み込むこのような接触データは数値の配列( 行列 )です(下図を参照).
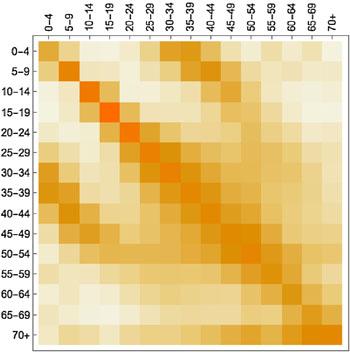
異なる年齢グループ間の平均的な接触を表示する接触行列.濃い色はより多くの接触を示します(ここでは,理解しやすくするために,数値ではなく色が使用されています).Contagion! The BBC Four Pandemic – The model behind the documentary.
学校閉鎖などの特定の社会的介入が,感染拡大にどのように影響するかを確認するには,介入に関連する部分を削除または縮小して,接触データを適宜調整してみます.
学校要因を完全にオフにするのは現実的とはいえません.減じるだけです.学校外で子供たちは,他のルートがあり(祖父母と混ざってしまう可能性など)ます.これは,考慮に入れるべき追加の接触が発生していることを意味します. 教師のストライキ中に起ったことなどの既存データは,接触データを補正し介入による流行への影響予測に役立ちます.
モデルが現実的であるかどうかは重大な問題です.COVID-19は新しい病気.既存モデルは季節性インフルエンザのために開発したもので,コロナパンデミックモデルは誰も作っていませんでした.COVID-19とインフルエンザとではモデルのどこが違うのかを調べなければなりません.
パンデミックのダイナミクスは,インフルエンザとコロナウイルスで似ていますが,違いもあります.
COVID-19はかなりの潜伏期があり,何の症状も示さずに感染している可能性があります.発症までに,インフルエンザの場合は数時間,コロナウイルスの場合は数日かかる可能性があります.
モデルに関して言えば,これは,SIRではなく,SEIRのモデルになることを意味します.Eは「露出」.
クラスEの人々は感染していますが,まだ症状は出ていません.クラスEの人は,他人に感染させる人と感染させない人に分けられます.すべてのモデルは近似であり,インフルエンザの場合は,目的によってSIRを回避できることがよくあります.ただし,コロナウイルスの場合,潜伏期間を無視すると,近似が非常に悪い.特に,短期予測のときは,これを考慮する必要があります.
COVID-19については,私たちが知らないことが他にもたくさんあります.1日目や2日目の感染力など,詳細はわかりません.不完全なデータからそれを推測するのは非常に難しい.中国や他の国のデータがいくつか(クルーズ船からのデータは非常に興味深い)あり,限られた情報から推測するのに最善を尽くしています.十分な情報がない場合,モデラーは不確実性を取り除くために,最も重要な未知数は何か決定します.これがモデリングで非常に重要なことです.
明日,何人の患者が出るか予測するなら,多くのことを知る必要はなく,現時点では指数関数的増加です. しかし,第2波が発生するかどうかを予測するには,非常に異なるいくつかのことを知る必要があります.
長期予測で重要なパラメータは,疾患の再生産数(1人の患者が平均何人に感染させるか.多くの場合,R_0と表示される)です.これは 感染速度に関連する.COVID-19の場合,R_0は2~2.5の間にあると推定されます.モデラーは,可能な値の範囲ごとにモデルを実行し,対応する予測の範囲を考えます.
感染したが病気ではない
多くの疫学者が知りたいもう1つの重要なパラメータは,集団内での感染の症例数で,これには,病気にかかったが症状を示さない人々の症例数も含まれます.無症候感染者数は,睡れなくなるほどの多数で,これを知ることは,私たちの出口戦略にとって非常に重要です.とGog氏は語りました.
現在の指数関数的成長を止める要素が2つあります.
1つは,学校の閉鎖や身体的な距離をとるなどの介入うぃして接触率を減らすことです.
2つ目は,罹患感受性のある人をなくすことです.病気になったらしばらくの間免疫があるので,無症候性を含む真の症例数を知ることから,罹患感受性の高い人々のクラスがどれほど速く減少するかがわかります.
議論されている集団免疫のメカニズムは,罹患感受性のある人数が減少するにつれて,病気の指数関数的成長が平担になり,指数関数的減衰になるという仕組みのことです.
幸い,無症候性に関するデータは知ることができます. 病気に罹ったか罹っているか抗体検査が実施されています.これらの第一波は当然NHSスタッフにのみ公開されます.
では何が起こる?
何が起こるか誰も正確に言うことはできません.地平線に見える大きな望みはワクチンの到着です.これは,集団に免疫を備えるもう1つの手段です.最も脆弱な人を優先的に,最小限のダメージでどのようにその目標に到達させるかです.誰もが同意するのは,これには長期的な犠牲が伴うということです.「1週間だけシャットダウンして,この状況がなくなることを期待することはできません」「社会的距離の措置が早すぎる場合,感染かまだ残っていて,集団免疫はありません.現時点では,ヘルスケアシステムが容量を超えないようにするために,シャットダウンせざるを得ませんが,これは恒久的な戦略ではないことは十分に認識しています」とGog氏は語る.
先週 ,Gogの元博士課程の学生であるスティーブンキッスラーとハーバード大学の同僚によって発行された論文では,季節変動も考慮して,再発の問題について詳細に検討しました.呼吸器疾患の発生は,秋と冬に悪化する傾向があります.季節性インフルエンザの発生と同時に,ヘルスケアシステムにさらに大きな負担をかけます.キスラーと彼のチームは,そのような季節変動を反映する要因を含むSEIRモデルを使用しました.社会的距離測定の効果は,COVID-19の基本的な再生産数が最大60%減少することでモデルに反映され,中国で観察されたものと同等です.
この最新の研究の結論は,必ずしも明るいものではありません.
「シリアルロックダウンの期間を検討しています」とGog氏は言います.(医療崩壊が始まろうとしているときにロックダウンするという考え)英国のナイチンゲール病棟NHSのことは,noteの記事の1号に書きましたので,そちらをご覧ください.
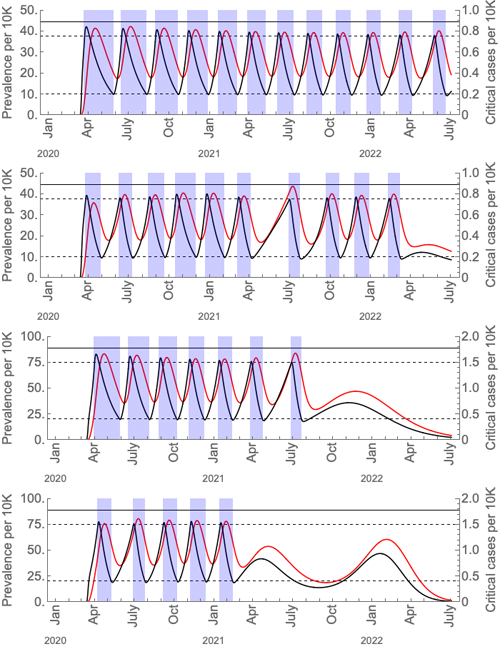
社会的距離(ロックダウン)の断続的な期間の長さと頻度の仮定(米国の数値に基づく)のシミュレーション.
これらのグラフは,断続的な社会的距離(青色の領域)の下でのウイルスの有病率(黒い曲線)と重症なケース(赤い曲線)を示しています.最初と3番目のグラフには,季節的な強制がありません.2番目と4番目の季節の強制.ケア能力臨界は,水平の黒い実線で示されます.最初の2つのグラフは現在の米国の救急医療能力でのシナリオ,3番目と4番目のグラフは現在の救急医療能力の2倍のシナリオです.再生産数の最大値は冬期は2であり,夏期は1.4です.この図は,キスラーらによるCOVID-19の流行を抑制するための社会的距離戦略の論文からです.
悲観的状況の中に,希望の光がいくつかあります.1つは,COVID-19の重症例に対して,投薬と良い治療プロトコルが,ある時点で追いつく可能性があることです.これで,NHSへの負荷の軽減でき,重症患者のケアができるます.
もう1つの希望の光は,軽度で無症候の感染者が,想定されているよりもはるかに多い(多くの人々がすでに病気になり免疫力がある場合)かもしれません.私たちはこれが事実かどうかわかるまでは,ルールを守って家にいるだけしかできません.