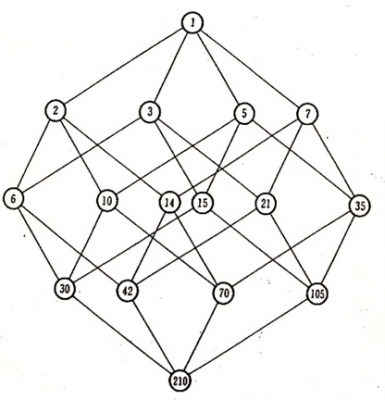
2019.10.26に開催した数学月間企画講演会では,約数の構造をわかり易く表示するグラフ(亀井図)を取り上げました.例えば,210の約数の系統的な構造を示すグラフは以下のようです.
210は4つの互いに素な素数の積210=2・3・5・7から出来ているので,4次元超立方体と同じこのような構造になります.210の約数は,自分自身の210と1を含めて全部で16個ありますが,系統的に並べると上の図のように整理できます.
頂点1のレベルには1個,頂点2のレベルには4つの素数,頂点6のレベルには2つの素数の積で4C2=6個,頂点30のレベルには3つの素数の積で4C3=4個,頂点210のレベルは4つの素数の積で1個です.4次元の超立方体には対称心があり,互いに点対称な頂点の積は210になることも理解できます.
このようなグラフは,数学のいろいろな分野で出会います.半順序を表現するハッセ図というのは,このグラフを逆順に描いたものと同じです.
210の約数の構造といえば,210をトップに置き逆順(ハッセ図と同じ)に並べる表示もありでしょう.
約数の構造に関しては,数学Aの研究課題として高校生にもなじみやすいものであるし,このグラフは高次元立方体の理解にも役立ち興味深いでしょう.
(注)数学ではハッセ図と呼ばれるものですが,美しくバランスのとれた4次元立方体は,亀井のアルゴリズムで描けるので亀井図とも呼ばれます.
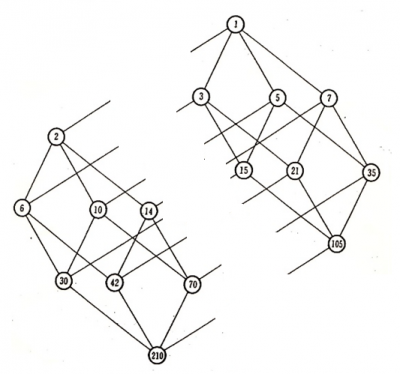
4次元の超立方体の1つの次元(例えば,素数2の方向)を消すと,3次元の立方体の2つに分離します(下図).同様なことを,それぞれの3次元立方体で考え,例えば,素数7の方向の次元を消すと,3次元の立方体は2次元の面(例えば1-3-15-5)に分離します.このような性質は高次元の超立方体の成り立ちの理解に役立つでしょう.
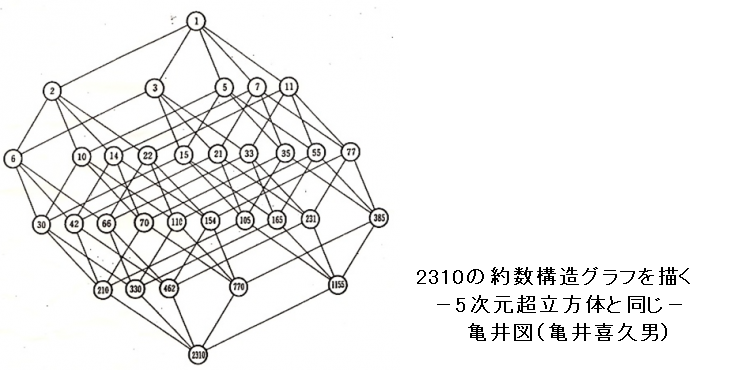
(演習)2310=2・3・5・7・11ですから,2310の約数の構造を示すグラフを描いてください.これは5次元の超立方体になるはずです.
解答
(演習) $$420=2^2・3・5・7$$ の約数の構造を示すグラフを描いてください.