■5つの正多面体(プラトン立体)のうちで,最も面の数が多い(球に近い)ものは正20面体です.正3角形の面が20個でできています.最も対称性が高いものという言い方も間違いではありませんが,互いに双対な正12面体と正20面体は同じ点群です.互いに双対な正6面体と正8面体は同じ点群です.
(注)正多面体とは,正多角形(正p角形)の面でできていて,どの頂点の周りも同数の面(q個の面)が会している立体です.この立体を,シュレーフリの記号で{p,q}と記述します.pとqを入れ替えた正多面体どうしを互いに双対と言います.
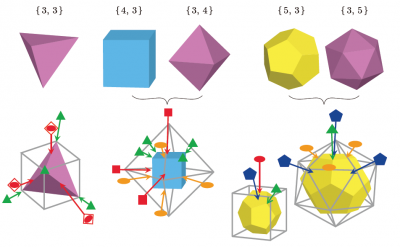
正多面体(プラトン立体)は,正4面体{3,3},正8面体{3,4},正6面体{4,3},正12面体{5,3},正20面体{3,5}の5つしかないことは証明できますから,面数20より多い正多面体が存在するはずはありません.
しかし,例えばゴルフ球のディンプルはいくらでもたくさん作れるように思えなす.正多面体の面を分割し続けると,いくらでも球に近い正多面体が作れるように思うかもしれません.しかし,そのようなことが可能なはずがありません.ここで作るいくらでも球に近い多面体は,面が正多角形からわずかに歪むので,正多面体ではないのです.
正20面体の1つの正3角形の面を4つの三角形に細分化します.このとき,中心の三角形は正3角形ですが,その周りの3つの3角形は正3角形から歪むのを確認ください.以下,細分化の操作を繰り返すたびに,面の数は4倍ずつ増加します.そして,細分化された面で正3角形のものは,初めの正20面体の面の中心にあるものだけです.だから,正20面体を細分化して,球に近い多面体を作っても,その対称性は正20面体と同一(細分化しても対称性は上昇しません).素性は隠せないのです.細分化された多面体の面は正3角形ではないので,細分化でできる多面体は正多面体ではありません.(この細分化で用いたjavaプログラムは郡山彬氏が作成しました)
美しい幾何学p.23より