新型コロナウイルスCovid-19の感染拡大が止まりません.皆様お元気でお過ごしでしょうか.現在,日本では「人と人との接触機会を8割減にしよう」との呼びかけがなされています.規制を遵守し感染機会を減らすことはこの時期非常に重要です.
8割減は,感染拡大の転換点であるとされています.その根拠となる手法の総説には,例えば,「感染症流行の予測:感染症数理モデルにおける定量的課題」(西浦・稲葉;統計数理,第54巻第2号,461-480,2006)があります.しかし,接触機会8割減が転換点であるという具体的なシミュレーションはまだ見ておりません.
いろいろな感染症はそれぞれの特異な伝染状況があり,それに合わせた数理モデルを作る必要があるので一般論ではかたづきません.Covid-19の感染拡大に対しての数理モデルと,感染率,ウイルスの活性期間,患者の死亡率,感染者が感染源になりうる期間,等々の係数を仮定する必要があります.Covid-19は,まだ解明されない特異な感染の振る舞い(無症状の保菌者が感染源になる,感染回復後も再度感染する,等々)があり,完全な数理モデルができず確定的予測は困難です.
今回,石黒真木夫が,簡単な仮定に基づくCovid-19の特徴を考慮した数理モデルを作り,教育的なシミュレーション結果を得ました.その詳細は.「NPO数学月間の会」のホームページhttp://sgk2005.saloon.jpにありますのでご覧ください.
■ここでは,数式を用いずに,石黒の数理モデルとシミュレーションの内容要点を紹介します.
(1)ある人口集団を未感染者,ウィルス感染源,免疫獲得者,死亡者に分類し,未感染者がウィルス感染源の一員と接触したときにある感染確率で未感染者が感染してウィルス感染源となるものとする[実際は,Covid-19では,人-物ー人の感染ルートもあるといわれる].
(2)ウィルス感染源のウィルス拡散は14日間つづき,14日目に「死亡率」に従って死亡者と免疫獲得者に分かれ,免疫獲得者はもはやウィルスを拡散することも再感染することもなくなる[実際は,再感染するケースも稀にある].
(3)このモデルでは時間の経過とともに未感染者は単調減少,免疫獲得者は単調増加するので,感染の流行はかならず止まる.しかしそれは集団全員が感染した後である.
(4)感染確率と死亡確率を適当に与えればシミュレーションは簡単である.いまの計算機をもってすれば人口集団の各個人の命運をたどるミクロ・シミュレーションもさして難しくないが,以下で紹介するのは未感染者やウィルス感染源集団の大きさの変化を追跡するマクロ・シミュレーションである.確率的な現象の「期待値の動き」を追いかける決定論的なダイナミクスを採用する.ミクロ・シミュレーションをして,算術平均の変化を見るとマクロシミュレーションの結果に「誤差」が乘ったような動きになるだろうと考えられる.
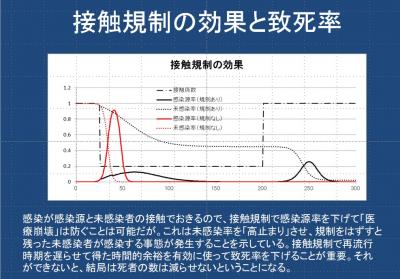
(5)感染が感染源と未感染者の接触でおきるので,接触規制で感染源率を下げて「医療崩壊」は防ぐことは可能だが,これは未感染率を「高止まり」させ,規制をはずすと残った未感染者が感染する事態が発生することを示している.接触規制で再流行時期を遅らせて得た時間的余裕を有効に使って致死率を下げることが重要.それができないと、結局は死者の数は減らせないということになる.
■石黒の数理モデルを用いたシミュレーション・プログラム(Excelファイル)は,NPO数学月間の会のウエブサイトhttp://sgk2005.saloon.jpに公開しています.各自このファイルをダウンロードし,パラメータも色々変えてシミュレーション実験をすると面白いだろう.各種規制の効果は接触機会数に乗じるパラメータを変えて見ることができます.
感染者数のピークが過ぎても,揺れ戻しの感染者数の小さなピークが観測され,このような波動を繰り返しながら収束に向かうことがわかるでしょう.