正4面体の２分割

Q．正4面体を，平面を切り口に，合同な２つの図形に分割すること．

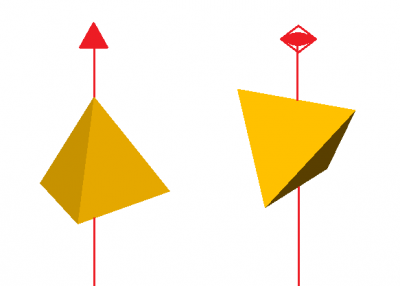
この問題を考えるのに，まず，正四面体の対称性から説明を始めましょう．図を見てください．正4面体の回転対称軸を調べると，3回回転対称軸が，各頂点にあります．2回回転対称軸は直角に対向している稜の中点を通ります．正4面体の場合は対称心もあるので，2回回転対称軸は，4回回反軸の性質もありますが，今，この問題で必要なのは2回回転対称軸の性質で十分です．鏡映対称面もありますが，この問題では関係ないので略します．

正4面体を，平面で切って，2つの合同な部分に2分割するのですが，対称性を考慮すると，2回回転軸を含む平面で2分割すると，合同な２つの部分に分割できることが理解できるでしょう．例えば，以下の2つの解答例を思いつきます．ついでに，Q．それぞれの例の場合に，その切り口の形はどのような図形でしょうか？という問題も追加します．

解答例１（指で挟んでいるのが，2回軸の正4面体への入口と出口）

解答例２（指で挟んでいるのが，2回軸の正4面体への入口と出口）

■さて私が言いたいのは，「解答例はそれだけでしょうか？」ということです．

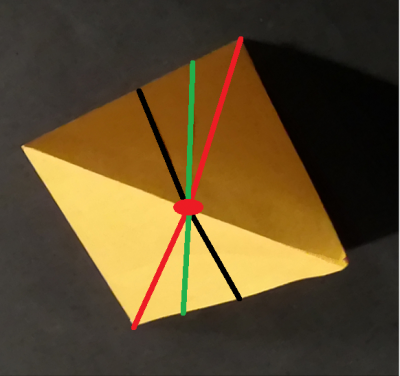
実はそのような解は無数にあります．一つの直線を含む平面は無数にありますから，どれも解になります．下図（正4面体の1つの2回回転軸の真上から眺めた図）をご覧ください．黒い線が表現する平面は解答例１，赤い線が表現する平面は解答例２の場合です．2回回転軸を含む平面は無数に作れるので，例えば緑の線も解答例になります．

私がこの問題を作ったのは，対称性の概念は，物事を見通し良く整理して理解するのに役立つことを示したかったからです．