https://elementy.ru/posters/fractals/Sierpinski
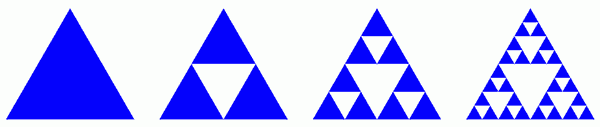
このフラクタルは、1915年にポーランドの数学者シェルピンスキーVaclavSierpinskiによって記述されました。これを作るには、正3角形の内部に、中線3本を引き、生じた4つの小さな3角形の中央の1つを捨てます。次に、残りの3つの三角形のそれぞれについて同じ手順を繰り返します。この図は、最初の3つの手順を示しています。
Sierpinski三角形を作る手順
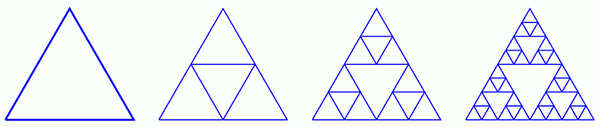
中央の3角形を捨てることは、Sierpinskiの3角形を作る唯一の方法ではありません。「反対」のやり方も可能です。最初は「空の」三角形を取り、その中の中線で形成される3角形を作り、3つの角の三角形のそれぞれで同じことを行います。最初は、図は大きく異なりますが、反復回数が増えるにつれて、それらはますます互いに類似し、無限回繰り返す極限では両者は一致します。
Sierpinski3角形を作る「反対」の手順
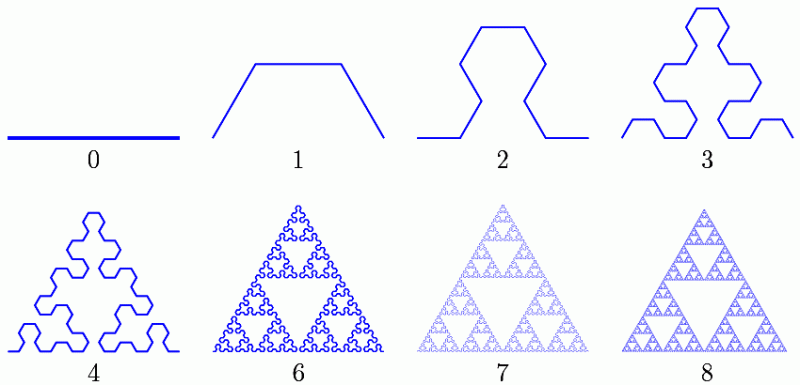
Sierpinski3角形を得る次の方法は、次の反復の一部に縮小された自分を置き換えることで幾何学的フラクタルを構築する通常の手順にさらに似ています。各ステップで、ポリラインを構成するセグメントが3つ折れのポリライン(最初の反復で形ができた)に置き換えます。この3つ折れを右と左に交互に置き換えて行きます。8回目の反復でフラクタルに非常に近いものが出来上がっています。
Sierpinski3角形を得る別の方法
しかし、それだけではありません。Sierpinski3角形は、平面上の点のランダム歩行の種類の1つの結果として得られます。この方法は「カオスゲーム」と呼ばれています。他のいくつかのフラクタルはそれを使って構築することができます。
カオスゲーム
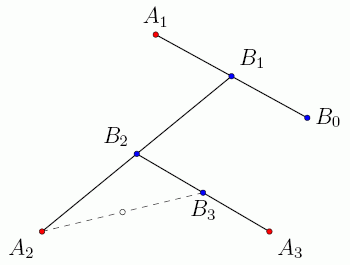
「ゲーム」の本質は次のとおりです。正3角形をA1 A2 A3とします。任意の始点 B0が与えられます。3角形の3つの頂点の1つがランダムに選択され、もしA1が選ばれたとすると、B0とA1の中点B1 がマークされます。同様に、次にA2が選ばれたとすると、B2がマークされます。その後、A3が選ばれたとすると、B3がマークされます。つまり、前の手順で何を選択したかに関係なく、三角形の頂点がランダムに選択されるたびにマークされる点がジャンプして生じます。驚くべきことに、シェルピンスキーの三角形がすぐに表示されるようになります。以下に、100、500、2500ポイントがマークされたときに何が起こるかを示します。
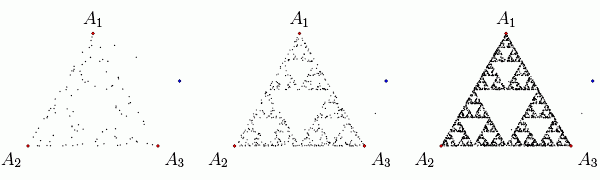
カオスゲーム:100、500、2500ポイント
いくつかの性質
フラクタル次元$$log_{2}3=1.584962・・・$$。 Sierpinski3角形は、自分自身を1/2に縮小した3つのコピーで構成されます。それらの相対位置は、グリッドセルが半分になると、フラクタルと交差する正方形セルの数が3倍になるようなものです。つまり、$$ N( δ/2)= 3N(δ)$$です。最初のセルサイズが1で、フラクタルがそれらの$$N_{0}$$と交差する場合($$N(1)=N_{0}$$), $$N(1/2)=3N_{0},N(1/4)=3^2N_{0},・・・, N(1/2^k) =3^k$$ $$N_{0}$$。 したがって、$$N(δ)$$は$$ (1/δ)^{log_{2}3} $$に比例しており、フラクタル次元の定義により、次元は$$log_{2}3$$に等しいことがわかります。
Sierpinski3角形の面積はゼロです。これは、単一の、非常に小さな円でさえ、フラクタルに収まらないことを意味します。つまり、最初の方法で構築を開始した場合、内部全体が3角形から「取り出され」ました:各反復のたびに、残っている領域は3/4倍されます。つまり、ますます小さくなり、0に収束します。これは厳密な証明ではありませんが、他の構築方法も、この特性が真実であるという確信を高めるだけです。
コンビナトリクスとの予期せぬつながり。$$2^n$$ 本の線があるパスカルの三角形で、すべての偶数を白で、奇数を黒で着色すると、目に見える数字はSierpinski3角形を形成します。
オプション
Sierpinskiによるカーペット(正方形、ナプキン)。正方形のバージョンは、1916年にVaclavSierpinskiによって記述されました。彼は、自己交差することなく平面上に描くことができる曲線は、このスカスカの正方形のサブセットと同形であることを証明することができました。3角形のときと同様に、正方形はさまざまなデザインから取得できます。右側は古典的な方法です。正方形を9つの部分に分割し、中央の部分を捨てます。次に、残りの8つの正方形についても同じことが繰り返されます。
Sierpinskiカーペット、最初の5回の繰り返し
3角形と同じに、正方形の面積はゼロです。シェルピンスキーカーペットのフラクタル次元は、3角形と同様に算出し log_{3}8
シエルピンスキーのピラミッド。Sierpinski3角形の3次元類似物の1つ。起こっていることの3次元性を考慮して、同様に構築されます。1/2に圧縮された最初のピラミッドの5つのコピーが最初の反復を構成し、その5つのコピーが2番目の反復を構成します。フラクタル次元はlog_{2} 5です。図の体積はゼロです(各ステップで、体積の半分が破棄されます)が、表面積は反復ごとに保持され、フラクタルの場合は最初のピラミッドの場合と同じです。
メンガーのスポンジ。Sierpinskiカーペットの3次元空間への一般化。スポンジを作成するには、手順を無限に繰り返す必要があります。繰り返しを構成する各立方体は、27個の1/3に縮小された立方体に分割され、中央の立方体とその6つの隣接する立方体が破棄されます。つまり、各立方体は20個の新しい立方体を生成します。これは3分の1です。したがって、フラクタル次元はlog_{3} 20です。このフラクタルは普遍的な曲線です。3次元空間の曲線は、スポンジの一部のサブセットに対して同形です。スポンジの体積はゼロですが(各ステップで20/27倍されるため)、表面積は無限大です。