空間を隙間なく埋める多面体★

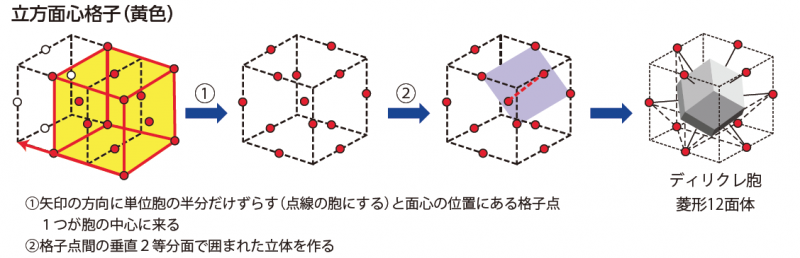
◆立方面心格子→菱形12面体
面心格子のディリクレ（ウイグナー＆ザイツ）胞を作図すると「菱形12面体」が得られます．

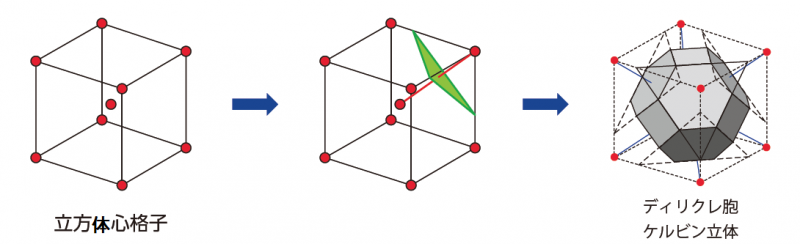
◆立方体心格子→半正多面体［4,6,6］（ケルビン立体とも呼ばれる「切頂正8面体」の一つ）
体心格子のディリクレ（ウイグナー＆ザイツ）胞を作図すると，この立体が得られます．

．

■格子というのは，無限に続く周期的構造の＜幾何学的表現＞です．格子点に置くのは繰り返される単位モチーフです．格子点に本当に点を置くのは一番単純な構造です．面心格子の格子点に本当に原子を配置した構造は，銅やアルミニウムなどの金属結晶で知られています．体心格子の格子点に本当に原子を配置した構造は，鉄，タングステン，セシウムなどの金属結晶で知られています．

■格子からディリクレ胞を作る手順を見ると，ディリクレ胞とは格子点１つが占有する多面体の形なのがわかります．
従って，格子点にディリクレ胞を配置すれば，空間が隙間なく充填されるのは明らかです.
そして，ディリクレ胞の対称性（点群）に格子の対称性が現れています．

図は省略しましたが立方体（角砂糖）を積み上げた形，菱形12面体や，ケルビン立体，は周期的空間を隙間なく埋め尽くすことができます．これら３つの対称性は同じです．

◆純粋に数学的に空間充填構造を導くのはとても大変なことですが，結晶学者は昔から知っていました．
自然科学の分野に数学への源泉がいろいろありました．結晶点群や空間群なども化学や鉱物学で発展し数学に貢献した例です．