PCR検査の統計と論理 谷 克彦
(要旨)
◆PCR検査の感度と特異度は,遥かに1に近い確率でした.偽陰性や偽陽性を理由に検査数をコントロールする理由は成り立ちません.検査を拡大し有病者を発見し早期隔離しましょう(感染から5日目頃が最もウイルスを放出し,有病者の半減期は10日位です).◆日本の陽性率は7%と計算できますが,最近の変動の勾配(末尾に掲載)から見ると10%を越えたように見えます.このグラフがそのように見えるのは,検査数を抑制しているために陽性者数のオーバーフローが起きている証拠かもしれません.
---------------------------------
COVID-19パンデミックは,実効再生産数を1より低下させると鎮まります.この対策は,次の3つの数値を下げることです;①感染者が感染力を持つ期間,②感染者が接触する人数,③感染者との接触で感染する確率.そして,それぞれに対する施策は以下のようです;
①感染者を早期に発見し隔離する.このためにPCR検査の拡充が必要.
②効果的なロックダウンの期間,地域,方法を,シミュレーションで予測し戦略的に介入する.
③ワクチン接種で,感染感受性のある人の割合を減らす.
COVID-19に感染すると,次のような経過になります.
感染(陽性)→潜伏無症状期→発症期(無症状もありうる)→回復(陰性)or死亡
陽性の期間[潜伏無症状期+発症期(無症状もありうる)]は,「罹患者」が感染源となる有病状態なので「有病罹患」と呼ぶことにします.感染源となる「有病罹患」(症状の有無にかかわらず)を早く発見し隔離する必要があります.
有病罹患者の発見はPCR検査でなされます.検査の目的は蔓延率の推定だけではなく,感染源となる有病罹患者をできるだけ早期に探し出し隔離するという緊急な役割があります.検査対象を限定し,検査の陽性的中率を上げることが検査の目的になってはいけません.
実世界の現象は,多数の原因と結果が複雑に絡んだ因果関係をなし,数学(統計)で論理的に推論するのは,その一部を切り取った世界です.その範囲で得た数学(統計)的推論の結果を,系全体の中で解釈できる論理的な思考が必要です.
正しい数学(統計)推論で得られた結果でも,複雑な全体系で非論理的に利用されるとしたら,社会を誤った方向へ導く主張に,数学が加担してしまうことになります.PCR検査の規模拡大は有病率の低い集団ではすべきではないというのは正しい主張ではありますが,その主張の根底にあるPCR検査の性能から見直し,これを論理的に考察してみましょう.
■有病率とは
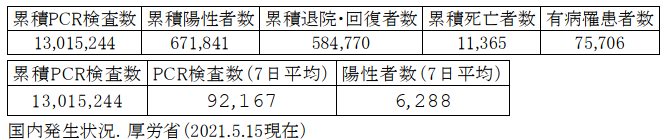
日本感染症学会の定義によると,有病率とは,「その疾患をもっている人数の全人口に対する割合」ですが,日々発表される厚労省の新規陽性者数と検査数のデータから,日本の有病率を計算できるように,有病率$$x_{0}$$の解釈を次のようにします.
(定義)$$有病率=有病罹患数/累積PCR検査数$$
$$有病罹患数=累積検査陽性者数-累積回復退院者数-累積死亡者数$$
これにより,日時($$T=$$5月15日)の日本の有病率を求めると$$x_{0}=0.58$$%になります.
ここでは,陽性者=罹患者と見なしています.
この検査集団の陽性率($$T$$)と罹患率($$T$$)は,7日平均(8~15日)を用いて,
$$陽性率(T)=陽性者(T)/検査数(T)=6288/92167=0.068$$,
罹患率(*)$$(T) =陽性者(T)/累積検査数(T)=6288/13015244=0.0005$$
日時$$T$$の有病罹患数$$(T)$$を別の定義で表現してみましょう.有病罹患状態は,14日位で回復(陰性になる)します(運悪く死亡の場合もありますが,少数のため無視します).今日$$T$$の有病罹患者(感染源となる罹患)の中には,$$t$$日前に罹患した者も残っています.そこで,次の定義が成り立ちます:
有病罹患数$$(T)=\displaystyle \int_{0}^{T}$$罹患数$$(t)p_{a}(T-t)dt$$,
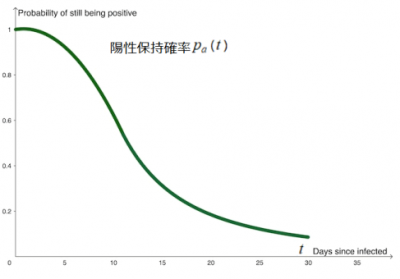
ここで,$$p_{a}(t)$$は,陽性保持確率(病気の減衰関数のような性質)で,(付録3)の大規模調査の結果に報告されています.病気の感染初日を推定するのは大変難しいのです.PCR検査で見つかった日が感染日という訳ではないでしょう.感染から5日目あたりが,感染者が最も多くウイルスを放出するので,その頃が最も発見され易いのではないかと思います.
病気減衰関数の半減期は約10日ですので,コンボリューション積分は次のように近似できます:
有病罹患数$$(T)=10×罹患数(T)$$.この集団の累積検査数で規格化すると.
$$有病率(T)=10×罹患率(T)$$が得られます.
注*)感染症学会の定義では,罹患率の分母は,「集団の感受性のある人数」ですが,ここでは「集団の人数」としています.
■PCR検査の感度と特異度
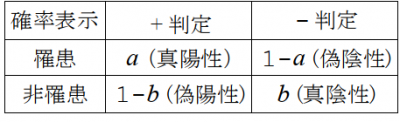
PCR検査の感度$a$とは,罹患者をPCR検査で陽性($$+$$)と正しく判定する確率のことで,真の罹患者でもPCR検査が陰性($$-$$)(偽陰性)と判定される確率は$$1-a$$程度あります.検査の特異度$$b$$とは,非罹患者を正しく陰性($$-$$)と判定する確率のことで,非罹患者を陽性($$+$$)(疑陽性)と判定する確率は$$1-b$$程度です.
確率$$a , b$$は1に近いほど,優秀な検査になります.従来の議論に用いられてきたこれらの数値は,$$a=0.70, b=0.99$$ですが,昨年の英国ONSによる大規模調査(付録3.)で判明した数値は,$$a=0.95(0.85 ~ 0.98)$$,$$b=0.9992$$です.
低い有病率の集団でPCR検査対象を拡大すると,莫大な偽陽性が出て医療崩壊につながるので,有症状者や濃厚接触者に限定して検査を行っているとの主張がありますが,英国ONS調査の感度と特異度を採用すると,この主張の根拠が覆えることを検証します.
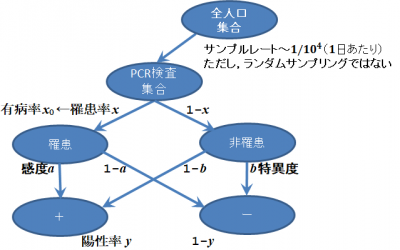
■ベイズ推定による有病罹患の内訳
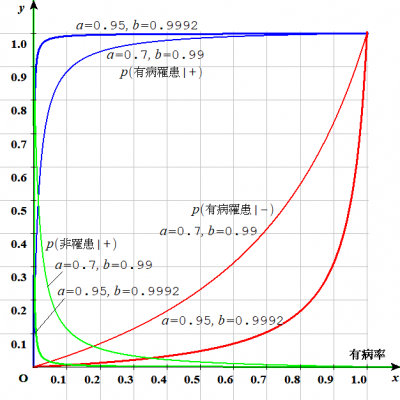
この集団の罹患率を$$p(罹患)=x$$,とします.この集団で,PCR検査が$$+$$判定のとき,罹患者である確率$$p(罹患|+)$$,および,$$-$$判定のとき,罹患者である確率$$p(罹患| - )$$,などを推定しましょう.
$$p(罹患| + )=p( + |罹患)・p( 罹患) /p( +) =a・x/( a・x+(1-b)( 1-x)) $$,
$$p(罹患| - )=p\left( - |罹患 \right) \cdot p\left( 罹患 \right) /p\left( - \right) =\left( 1-a \right) x/\left( (1-a)x+b\left( 1-x \right) \right) $$,
$$p(非罹患|+)=p\left( + |非罹患 \right) \cdot p\left( 非罹患 \right) /p\left( + \right) =(1-b)(1-x)/\left( (1-b)(1-x)+a \cdot x \right) $$,
$$p(非罹患| - )=p\left( - |非罹患 \right) \cdot p\left( 非罹患 \right) /p\left( - \right) =b\left( 1-x \right) /\left( b(1-x)+(1-a)x \right) $$,
下に$$x$$を変数とするグラフを示します.ベイズの定理は線形システムなので,重ね合わせができ,罹患状態を束ねた状態で定義される有病率$$x_{0}$$を入力にしても良いでしょう.
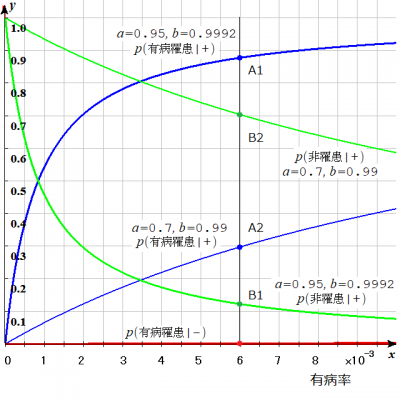
■集団の有病率 $$x=0.006$$に対して,感度$$a$$,特異度$$b$$を変えて比較
(1)$$a=0.95, b=0.9992$$(英国ONS)を用いた場合
$$p(罹患|+):p(非罹患|+)=真陽性:偽陽性=0.9:0.1$$
$$p(罹患|+):p(罹患|-)=真陽性:偽陰性=0.9:0.0003$$
(2)$$a=0.7, b=0.99$$(従来)を用いた場合
$$p(罹患|+):p(非罹患|+)=真陽性:偽陽性=0.3:0.7$$
$$p(罹患|+):p(罹患|-)=真陽性:偽陰性=0.3:0.002$$
PCR検査が$$+$$判定であるときに,真陽性の確率$$p(罹患|+)$$と,偽陽性の確率$$p(非罹患|+)$$を比較すると,従来用いられている感度,特異度では,偽陽性確率が真陽性確率の$$2.3$$倍もありますが,英国ONSの数値では,逆に1/10になり,医療崩壊を懸念する根拠にはなりません.
いずれにしろ,陽性確定までにPCR検査は2度行われ,さらに,抗原検査の併用もありますから,偽陽性の誤判定リスクは回避可能です.積極的にPCR検査の対象を拡大し,感染源となる無症状の罹患者を拾い出し早期隔離する道を閉ざすべきではありません.
次に,真陽性の確率$$p(罹患|+)$$と偽陰性の確率$$p(罹患|-)$$を比較すると,
(1)では,$$1:3 \times 10^{-3}$$,(2)では,$$1:7 \times 10^{-3}$$で偽陰性は小さい確率です.これを人数で比較するには,陽性率$$y=0.07$$,陰性率$$1-y=0.93$$を,それぞれ,$$p(罹患|+)$$と$$p(罹患|-)$$に乗じます.
(1)では,$$真陽性人数:偽陰性人数=1:4 \times 10^{-2}$$,
(2)では,$$真陽性人数:偽陰性人数=1:9$$
この集団の陽性率は$$7$$%と低いので,陰性集団が大多数で,偽陰性の確率が小さくても偽陰性者数は多いとの主張もあります.確かに,従来の数値(2)を用いると,真陽性者の9倍もの偽陰性者がいます.しかし,数値(1)を用いると,偽陰性者の数は1/100で,PCR検査対象を拡大しない理由にはなりません.検査を拡大すれば,拾い出せる陽性者は検査数に比例して確実に増加します.
■PCR検査数は十分か
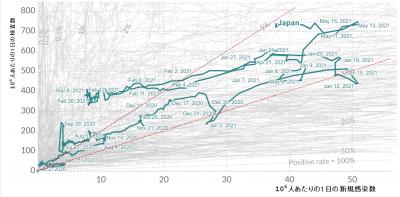
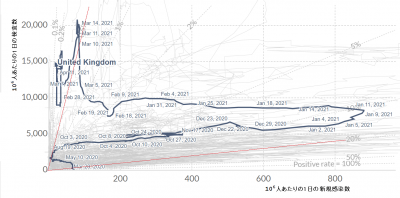
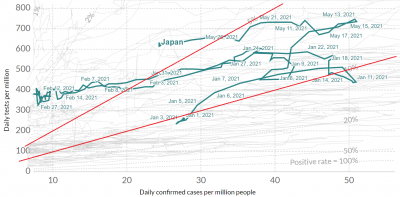
ここに引用した2つの図は,1日の$10^{6}$人あたりの(横軸)検査陽性数:(縦軸)検査数の散布図で,日本(上)と英国(下)の例です.英国の散布図スケールは日本のものより縦軸で25倍,横軸で16倍大きいのでご注意ください.散布図パターンを比較すると特徴的な違いがあります.時間経過とともに,右横あるいは右下がりに伸びる部分では,検査数が足りず陽性者の増加傾向を頭打ちにしている可能性があり,縦に伸びる部分では,陽性者を拾い出す十分な検査が行われているようです.英国の例を見ると,始めは,陽性者が多く検査数が間に合わないほどでしたが,現在みられる検査数を増しても陽性者が一定となる状態は,十分な検査数が確保されている証拠です.日本の例で,検査数と陽性者数の増減の比例が見られる傾向は,検査数を増やせば,陽性者数も増加する可能性があります.
これらの図は,2020.1.25~2021.5.25の期間のもので,赤細線は,日本の図では,陽性率5{\%}と10{\%}の勾配,英国の図では,0.5{\%}と20{\%}の勾配を示しています.
これらのグラフは,https://ourworldindata.org/coronavirus-testingから引用しました.
■付録-----
付録1.ベイズの定理
条件付き確率についての「ベイズの定理」とは次のように説明できます.
$$p(Y|X)p(X)=p(X \cap Y)=p(X|Y)p(Y)$$
ただし,記号の意味は例えば以下の様です.
$$p(X)$$:$$X$$が起こる確率
$$p(Y|X)$$:$$X$$が起きる条件下で,$$Y$$が起こる確率
$$p(X \cap Y)$$:$$X$$かつ$$Y$$が起こる確率
ベイズの定理は,$$X$$(原因)が起きる条件下で$$Y$$(結果)が起きる確率$$p(Y|X)$$と,$$X$$と$$Y$$を入れ替えた確率$$p(X|Y)$$を結び付ける定理です.
付録2.PCR検査の原理
PCR(ポリメラーゼ連鎖反応)を利用して,わずか数分子のターゲットDNAから数ミリグラムのDNAに増幅する技術を,1983年にマリスが発見し1993年のノーベル化学賞を受賞しました.
RNAに対しても逆転写酵素によりDNAを合成し,DNAの複製反応が利用できます.ターゲットDNA鎖全体の複製ではなく,ウイルスを特徴づける断片の複製をします.これが,パウエル社が発表(1987)したRT-PCR技術です.PCR検査は,検体に含まれるCOVID-19ウイルスの微量なRNAから,逆転写酵素を用いて,cDNAを合成し,温度サイクル処理を40回程度繰り返し,cDNAを検出可能な濃度まで複製するというものです.このようなPCR検査の原理から,検体にわずかでもターゲットRNAが含まれていればいくらでも増幅できますが,含まれていなければ誤混入がない限り増幅物は全く生じません.すなわち,特異度の高い検査です.
付録3.英国ONSのcovid-19感染の大規模調査
英国国家統計局(ONS)によるcovid-19の大規模感染調査は,パイロット調査としてイングランド(2020.4末)で開始されました.7月以降,規模を拡大し,住所リストから世帯のランダム・サンプリングを行い,8月には,2週間ごとにテストされるサンプルを,イングランドで15万人,ウエールズ,スコットランド,北アイルランドで各1.5万人の規模に拡げました.調査は,小児の症候性および無症候性感染の有病率と発生率を知るため,2歳以上の子供を含みます(参照:covid-19学校感染調査).16歳以上の成人の20{\%}は血液サンプルの提供を求められました.2020.7.31~9.10の6週間で,208,730の検体調査を行いました.偽陽性は症状のない人で発生すると予想されましたが,調査研究のデータからは,症状の有無によらず同じでした.血液サンプルは,オックスフォード大学で,抗体検査,IgG免疫グロブリンのテストをしました.
PCR検査に関する知見は;その感度が,85{\%}~98{\%}(95{\%}である可能性が最も高い)にあり,特異度は,99.92{\%}でした.
綿棒スワブの検体採取は,適切な監督下で行えば,自己採取でも医療従事者が直接採取した場合と同様の正確な結果になることも報告されています.
引用データ
1)厚生労働省
2) Coronavirus (COVID-19) Infection Survey, UK Statistical bulletins
3) Keeping up with COVID-19, Rachel Thomas;
https://plus.maths.org/content/keeping-covid-19
4) https://ourworldindata.org/coronavirus-testing