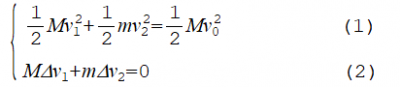YouTubeにある動画について.たいへん興味を引く動画なので,ぜひご覧ください.この動画の発信元3Blue1Brownは,Grant Sandersonが作ったYouTubeのチャンネルで,なかなかよくできた可視化された数学入門です.
動画は,物体mは静止しており,物体Mは初速度v0で摩擦のない台上を滑る所から始まります.
Mやmはそれぞれの物体の質量(M>m)で,左側は壁です.
衝突はすべて弾性衝突とすると,エネルギー保存(1)と運動量保存(2)が成り立ちます.
(1)は楕円の式ですが
の変数変換をすれば,新しい変数$$v_{3}$$を採用した$$v_{1},v_{3}$$平面では半径$$v_{0}$$の円になります.
(2)は,2つの物体m,Mが衝突したとき2つの物体から成る系全体の運動量が保存される(運動量変化が0)ことを示しています.こちらの式も,$$ v_{2} $$から$$v_{3}$$へ変数変換すると,$$v_{1},v_{3}$$平面で傾き-√M/mの直線になります.物体mとMの衝突後に分配される速度変化$$⊿v_{1}$$と$$⊿v_{2}$$の比は,それぞれの質量に反比例するわけですが,質量mの速度$$v_{2}$$を変換した$$v_{3}$$に対しては,$$v_{1},v_{3}$$の速度変化の比はそれぞれの質量の平方根に反比例します(2').つまり,$$ v_{3}=-\sqrt{M/m} ・v_{1}+C $$で,傾き$$-\sqrt{M/m}$$の直線です.
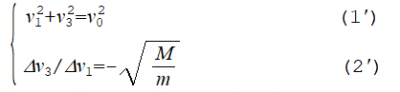
物体mが壁と衝突するときは,壁は動きませんから,$$v_{3}$$の符号のみ変えます.横軸を速度$$v_{1}$$,縦軸を速度$$v_{3}$$としてグラフを描くと,式(1')は,半径が$$v_{0}$$の円で,エネルギーが保存される系の状態はいつもこの円上にあるべきです.式(2')は運動量保存を示すグラフで,$$(-v_{0},0)$$の点から出発し傾き$$ー\sqrt{M/m}$$の直線です.
この直線が円と交差する点が,物体mと物体Mの最初の衝突後の速度$$v_{1},v_{3}$$の状態です.
その後,物体mはそのまま滑り壁に衝突し,$$v_{3}$$だけが符号を変えます.これは,最初の衝突点の$$v_{3}$$の符号を変えた円上の点になります.
このように続けると,円内に納まるのこぎり歯状のグラフができます.
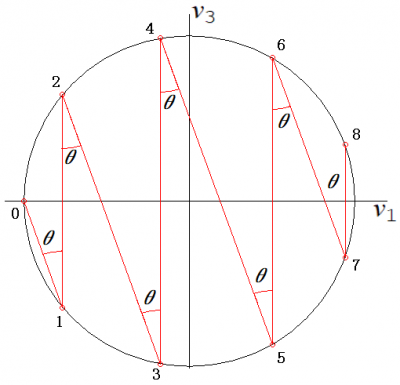
YouTubeのアニメーションのように,Mの質量を増加させると,直線(1')の傾きが急になり,のこぎり歯が細かくなるので衝突回数は増加します.
きちんと計算すると,$$tanθ=\sqrt{m/M}$$として$$\theta =\textrm{tan}^{\textrm{-1 } }\sqrt{m/M}$$,衝突回数Nは,N=2[π/2θ]となり(中心角2θだから),Mが大きくなればなるほど,Nは大きくなります.([]は数値の整数部分)
$$m/M=10^{-2p}$$とおくと,$$M$$が大きくなる($$p→∞$$)とき,$$N→π×10^{p}の整数部分になります.
上の数表のミソは,$$M/m=10^{2p}$$のときしか調べていないので,$$π$$の$$10^{p}$$ 倍の整数部分が並ぶことになる.