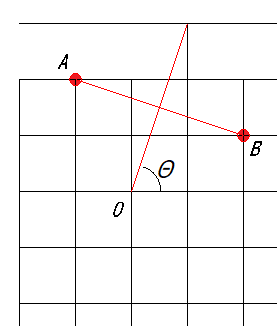
ある折り紙の本に正5角形の作り方がありました.
複雑な手順なので整理して原理だけ説明しましょう.
正5角形の中心角72度を作るミソは,以下のようです.
これで,Θは72°になることを証明できますか?
答,72°になりません.
約71.56...°です.
この折り紙手順で作れる角度は,72°に非常に近いので
実際の折り紙工作では非常に良い方法といえるでしょう.
でも,幾何の命題としては正しくないのです.
話は別になりますが,
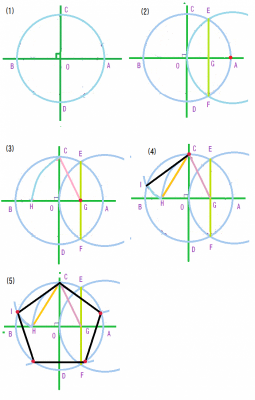
正5角形を,コンパスと直線定規で作図できます;
例えば http://www.natubunko.net/zukei/png/penta03.png
ここから図を引用しましょう.
さてそれでは,この作図を折り紙の手順で追いかけてみましょう.
折り紙の手法で,「円を描く」というのは,可能でしょうか?
コンパスの使い方には2通りあます;
1)所定の長さを所定の方向にとる.
2)2つの円の交点を求める
(与えられた2点から,それぞれ与えられた距離だけ離れた点を求める).
このうち,1)は折り紙手順で可能ですが,2)は折り紙手順で不可能ではありませんが工夫がいります.折り紙の手順で,正5角形の作図を追いかけてみると,(4)の段階で,2つの円の交点を求めることが必要になり,ここが困難です.でも不可能ではないようなので,皆様,挑戦されて,もし,うまい方法を発見したら教えてください.
まったく別の方法でも,折り紙で正5角形を作ることができます.例えば,表紙の写真は定幅紙(帯)を用いて正5角形を折ったものです.この場合はどのような手順の作図になるのかを考察してみてください.このような折り紙は手順が全部完成してからつじつまが合うように最初から調整しますから,漸近的に正5角形を得る作図のようなもので,無限の手順がかかるので幾何学の作図としては認められません.