proccessingという使いやすいオープンソースのプログラムがあります.私も使っています.現在はver.3.5.4が出ています.これで何ができるか粒子モデルの紹介です.
この記事は,英国MMPのplusマガジン42号(2004)の翻訳(訳:KT)です.
http://plus.maths.org/issue42/features/dartnell/index.html
Matrix: Simulating the world Part I - Particle models by Lewis Dartnell
鳥の群れが黄昏空に飛び交う様,魚群が敵をかわす様を見たことがあるなら,その完璧に振り付けられた動きに驚愕したことだろう.この行動は,
複雑に思えるかもしれないが,コンピュータでそのモデル化を行うのは,
それほど難しくはない.Lewis Dartnellが諸君自身のシュミレーションの
実地ガイドをする⇒経験不要.
粒子モデルにより,鳥の群れの運動,銀河系誕生,原子分子の物質構成,
などをシミュレート!
■マトリックス[訳注:1999年アメリカ映画]
世界をシミュレート 第1部---粒子モデル
モデルの構築は,科学や工学の多くの研究分野の核心である.
モデルの本質は複雑な系の表現であり,複雑な系のふるまいを理解するのに
異なった種々の方法で系の単純化がなされてきた.例えば,航空技師は,風胴テストのために戦闘機のミニチュア模型を作るかもしれないが,現代は,数学モデルをコンピュータ上でたいへん高速に走らせるモデリングが,ますます盛んになっている.超音速気流のコンピュータモデルは,信じられないくらい複雑だが,プログラムのデザインとシミュレーションは非常に基礎的な原理に基づいている.
モデルのふるまいに関するこの論文の前半で,たいへん興味深い自然系研究のコンピュータモデルが,いとも簡単にプログラムできることを述べる.
先端研究にこのようなモデルを用いている科学者の何と少ないことか.
◆はじめよう
http://plus.maths.org/issue42/features/dartnell/fish.jpg

Fig.1 どちらに行くのか?魚の行動をシミュレートする方法を見出せ.
これは,数学的なモデリングとコンピュータ・シミュレーションへの体験入門である.だが,プログラミングそのものの学習には深入りしない.これまでにプログラムを見たことがないとしても,心配は要らない.
シミュレーションのすべては,このウエブサイトでJavaビデオとして見ることができる.もし諸君がコンピュータプログラミングをすこしやったことがあるなら,この論文で用いた全コードをダウンロードして,改良したり調節したり試してみたいだろう.これらのシミュレーションを書いたり,アニメーション作りに用いたソフトウェアはプロセッシングと呼ばれ,無料でダウンロードでき,PCやMac バージョンで利用可能だ.
プロセッシングはコンピュータ科学者とアーティストの協力でリリースされ,自分で容易に改良や開始ができる.http://processing.org/download/index.html
プロセッシングが使われた世界中の種々のプロジェクトすべてのリストを
ホームページで一見されたし.http://processing.org/
よいモデルを組み立てる本質は,複雑な問題をいかにうまく単純化し,
系の重要な特徴を抽出し,モデルのふるまい解析を混乱させるものは取り除くように考えることだ.
例えば、ライフル銃から発射された銃弾弾道の単純なモデルは,明らかに重力の影響を考慮する必要があるが,空気抵抗のわずかな影響は無視してよい.この場合の空気抵抗は,2次オーダーの効果と呼んでよい.
別の系のモデリング,航空機の翼による揚力では,空気の影響を無視することはできないが他の因子は無視できる.
コツは,そのふるまいが理解しやすいように,モデルをできうる限り単純に保つことと,意味のない結果が生じないように重要と思われる因子をあまりカットしないようにし,入力因子の一つを変えて全系の応答の影響を見ることとのバランスにある.
この最初の論文のすべての例は,各点が空間内を色々な規則に従い動き回る粒子モデルとして知られるものである.
◆箱の中のガス分子
最初のモデルは,箱につめられたガス分子の大変基礎的な物理シミュレーションだ.見やすく単純にするため正方形内に閉じ込められた2次元粒子とする.この場合の物理は簡単である.各粒子は,箱の壁に当たるまで,
出発したときと同方向・同スピードで直線運動し続ける.壁に衝突すると,粒子は跳ね返り方向を変えるがスピードは変えない.映画と同じで,この論文のアニメーションは流体の運動を印象づけるフレームのシリーズからなる.
プログラムの仕事は各粒子の位置,方向,スピードを各時間ステップごとに前のステップの情報に基づき計算することである.この論文のすべての例では,各時間ステップごとのデータを配列または行列に蓄える.
行列の各行は異なる粒子に関する必要な情報を蓄える.このガスの例では,各粒子の状態は4つの数で記述される.
これらのうちの2つは平面内の位置(x,y)である.残りの2つは,粒子の運動の2成分を記述する.これらはdeltaX, deltaYと呼ばれる(”X位置の変化”,”Y位置の変化”の意).粒子の速度も定義する.
この場合の行列は4つの列と,全粒子に対する十分な行数を持つ.
シミュレーションの各時間ステップごとに,各粒子の位置(x,y)は,その速度に依存した更新を受ける.このプロセスのモデルを記述するプログラムの構造は,かなり直接的である.
どのように機能するか一般的な要点がつかめるかコードを見てみよう.
http://plus.maths.org/issue42/features/dartnell/Gas_molecules.pde
最初にするのは,モデルの最も重要なパラメータ(含まれる分子の数,各粒子の位置と速度の情報を格納する行列など)
の定義である.次に,プロセッシングは,世界の大きさ-この例では正方形,アニメーションのフレームレート-を決め,シミュレーションのセットアップをする必要がある.
それからシミュレーションの初期化をする.これはデータを蓄える行列で,各粒子の初期位置,速度の必要な情報を順次蓄える.今回は,粒子のランダム散布を選んだ.
次に,トルコ石色の背景と各粒子の(x,y)位置に置かれた赤い円で系の現状を記述するコードがある.
最後に,シミュレーションの中核,アップデート関数が来る.
各時間ステップごとに,この関数は,行列中の各粒子に順番にあたり,時間ステップ内に,その速度が箱の境界を越えその粒子を飛び出させないかどうか計算する.
もし飛び出すなら,箱の壁で跳ね返り,粒子速度は変化するが,そうでなければ,その速度ベクトルで決められる距離だけ前進し続ける.
かくして,各粒子は新しい位置と新しい速度ベクトルをもち,行列は新しい値にアップデートされる.
http://plus.maths.org/issue42/features/dartnell/Gas_molecules_web.jpg
Fig
箱に閉じ込められたガス分子のモデル.Java始動には映像をクリック.
全プログラムは,粒子が系をアップデートした後,再び描画し,
粒子はもう一度アップデートされ,これが繰り返されるように,
ループにセットされる.高速な現在のコンピュータでは,
これがたいへん高速に行われるので,ガス分子のスムーズなアニメーションになる.
この絵はプログラムのJAVAバージョンを開くようになっているので,
プロセッシングソフトウエアをインストールしなくても,動作を見ることができる.
この過剰に単純化したモデルは,2つの問題点があることに気づくだろう.第一に,我々のプログラムではdeltaX,deltaYに整数値だけ使っていること.このため粒子が動ける異なる方向の多くがなくなってしまう.
粒子のいくつかは,両サイドでバウンドし往ったり来たりするので,完全に水平や垂直に動くのが見られる.
第二に,このコードは,分子間の相互作用を考慮していない.分子は決して互いに衝突せず,箱の中を跳ね回るだけで,
完全予測可能である.周期的に,はじめがそうであったように,全分子が外向きに散らばる前に,真ん中で密なクラスターが形成される.これは明らかに部屋の中の空気分子では起こらないことだ.
空気分子は絶えず互いにぶっつかりあい予測不可能な運動を生み出している.
もし諸君が,少しコンピュータプログラム知っているなら,この単純な例をスタートとして,もっと洗練され現実的なものを作りたいと思うだろう.これをどのように行うかの若干の助言は,プログラムファイルの末尾にある.
運動のモデリングのもう一つの例に移ろう.今度は,粒子の相互作用の規則がもう少し複雑である.
◆鳥の群れ
モデル化する系は鳥の群れである.分子の例のように完全に独立に動くのではなく,各粒子は他の粒子の動きに反応して動く.
同様な標準構造をガスのプログラムにも用いるだろう.
最初はパラメータと世界の大きさを決め,全粒子の位置と速度を初期化する.次に,系の現在の状態を表示する関数のループをまわし,
次のタイムステップでの系の変化の計算を行う規則を実施する.
最初の例は,閉空間に閉じ込められた粒子の運動のシミュレーションをねらった.
今度は,開かれた戸外で飛ぶ鳥がどのように群れを作るか調べるのが関心事だ.エッジがあるような世界は困る.なぜなら,そのような人工的な特徴の周りでは,シミュレーションが適切にふるまわないであろうから.
モデリングの共通のコツは,世界空間を,粒子が左から去れば右から現れる,上下も同様[周期的境界条件]に世界空間を定義することだ.
上下は互いにつながりチューブのよう.左右端を丸く曲げてつなぐ.
ドーナツの表面の世界のようだ(数学ではトーラスという).
http://plus.maths.org/issue42/features/dartnell/flocking_index.html
Fig
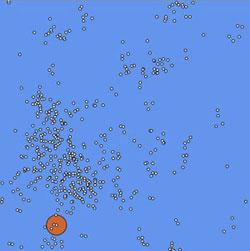
鳥の群れモデル.単純な規則の集合が,他の鳥との相互作用を定義し各粒子の運動に作用する.燈色の円は視野範囲を示す.イメージをクリックすると
シミュレーションのJavaバージョンが走る.
再スタートは[Ctrll]+[F5](Windows)または,[z]+[R](Mac).
このモデルでの第二の発展は,直線運動を続ける粒子のかわりに,
鳥たちは互いに相互作用をし近隣者に依存し飛ぶ方向を変化させることだ.
各時間ステップごとに,プログラムは,次々に各鳥を選び,選んだレンジ内で他のすべての鳥の飛行方向の平均を計算し,選んだ鳥はこの方向に舵をとる.
ランダムに選んだある鳥の視野レンジの場を燈色の円で表示させる.
プログラムで値を蓄える変数はeyeSight.
プログラムがどのように機能するか一般的な要点を拾い上げるため,
コンピュータ・コードを一寸見てみよう.
http://plus.maths.org/issue42/features/dartnell/Flocking.pde
次に左のイメージのシミュレーションを走らせて見よう.
始めはランダムであった鳥たちの運動が,直ちに秩序のある振る舞いに変わる.
鳥の巨大な群れが,大体同じ方向に飛び行くように自己組織化される.
孤立した鳥が一団の中に引き込まれる.そして時折2つの大きいグループがお互いに近づいて迷うとき,個々の鳥は他の群れに参加するために引き剥がされる.2つの雲がスムーズに混ざり合うようだ.
ちょっと迷って,そして次に新しいグループの先頭が決まる.
この設計された行動を本当の鳥一団の動的関係と比較してみよう.
これを書く時点で,あるホップベースの飲物の英国テレビで放映されている素晴らしい広告がある.
夕映え空のツバメの群れに魅せられる.タグ ライン「属します」で終わる.
この広告はYouTube から見ることができる.たとえすでに消されていたとしても,他の鳥の群れビデオを見いだすのは全く容易であろう.
http://www.youtube.com/watch?v=RHHfynLYW1I
Fig 巨大スケール鳥群れを示すYouTube広告
この運動は優雅な振り付けに見える.
個々の鳥が次に何処に飛ぶか正確に知っているように見える.
鳥の巨大な流れが,滑らかに調和し一斉に方向を変える.
群れの中にリーダーはいない.基本計画もない.
すべての決定はグループ力学だけで決まる.
何千という群れをなす鳥の魅了される複雑さのすべては,
最近接の隣を越えた残りのグループが何をするかを知ることなしに,
個人が行動するというたいへん単純な規則から発する.
これはボトムアップ制御として知られる.
単純な規則で相互作用している個体から,
たいへん複雑なグループ行動が出現する例だ.
たくさんの動物,ミツバチ,スズメバチ,アリ,シロアリ,...が,
この種の「群れ知性」を使う.
しかし,群れの振る舞いの基礎となっているこれらの単純な規則は異常な環境では,まったく馬鹿な行動を惹き起こすことがある.
自分自身ではまだ試す機会がなかったが,友達の友達から,
諸君が羊の一団と一種にやれる面白いトリックの信頼できる情報を得ている.
羊達の前で突然走ったとする.羊達は脅威を察知し動き去ろうとする.
まだ可能な限り,諸君の隣人に近い状態を保って,同じ方向に動作することが最も安全であるという規則は働いている.
もしあなたが羊より少し速く走り続けるなら,あなたは追いつき,
そして一団の中央を通過して先頭で今走っている.グループの動的力学が,
侵略者から逃げ出すという初期の個体の決断から引き継がれていて,
あなたは,群れ全体をあなたの後ろに従えていることになる.
◆コウモリとタカ
プロセッシングソフトとこのモデルのプログラッミングコードをダウンロードしたら,グループ全体のふるまいにどのように影響するかモデルのある特徴をいじることができる.
例えば,鳥同士は何処まで見えているのか,eyeSight変数はたいへん重要なパラメータだ.我々のプログラムでは,この変数は20にセットされている
(とりの視野を表している燈色の円の半径が20単位).
このパラメータは諸君の望む如何なる値にもセットできる.
2つの異なるシナリオを見てみよう:
”コウモリのように目が見えない”eyeSightは1とする.
もう一つは地図をよぎって見渡せる”タカの目”eyeSightは100とする.
下の2つのリンクの図をクリックすればjavaが動き,どちらのシミュレーションも見ることができる.
http://plus.maths.org/issue42/features/dartnell/eyeSight1_web.jpg
http://plus.maths.org/issue42/features/dartnell/eyeSight100_web.jpg
Figコウモリのように目が見えないeyeSight=1 タカの目eyeSight=100
第一のシナリオでは鳥たちは相互作用をまったくしない.だから実際は世界空間内でランダムに走るガス分子と同じだ.
第二のシナリオでは,鳥たちはグループの反対側にいる個々の鳥の飛行方向に反応するくらい,たいへん遠くまでコミュニケーションする.グループのふるまいはたいへん速く一体化した固まった運動になる.
どちらの場合にも,少なすぎるか多すぎる相互作用のために,すべての複雑な群れのふるまいは失われる.
系のアウトプットはこのパラメータにたいへん敏感である.気体的ふるまいと固体的なふるまいの間にある種の相転移がある.興味あるダイナミックスの見地ではどちらも死んだも同然だが,自然ではeyeSightの値がこれら両極端の中間値のときにのみ緊急行動が起こることが見られる.