4月25日,10:30から,Zoomを用いてリモートでの同志社中学校のDo★MATH博物館の見学がありました.10分間ほどの休憩をはさんで1時間ほど園田先生が出演され,見学会と,一太刀切りでハートや星形を作ったり,誕生日を当てる数あてカードを楽しみました.今年は,「数学月間」のイベント(毎年7月22日に実施し今年は第16回)もリモートで実施することになりそうです.
誕生日(1~31の数)を当てるには,4x4の数字が書かれた5種類のカードを見て,自分の誕生日が書かれているカードを選び出します.そして,それらのカードの左上の数を足し合わせると誕生日が当たるのです.
なかなか不思議ですね.この原理を今日は解説します.
■これからの説明は,誕生日を当てるゲームの変種で,15までの数を当てるゲームについて語りましょう.ゲームの実施方法も,数字が書かれてあるカードを選ぶのではなく,数字が書かれたカードの上にマスクをかぶせて当てようとしている数が見えているかどうか訊ねる方法になります.この両方のゲームとも同じ原理(2進数表記)を利用しています.
4x4の16個のマスに0~15の数字が書かれたカードがあります.このカードの上に孔のあいたマスクカードを重ね「あなたの思った数が見えますか」と尋ねる.これをマスクカードを変えて4回行えば,相手が心の中で思っていた数が当てられるというのが,この数当てのゲームです.
どのような仕組みがあるのでしょうか.秋山久義さんが,2019年7月のパズル懇話会で発表されています.今日は,秋山久義さんの発表「数当てカードの諸相」から引用して,その仕組みを解説します.
まず,16個の数の配列は,ランダムに配置したふりをしていますが隠れた規則があります.
例えば次の2つの方法があります.
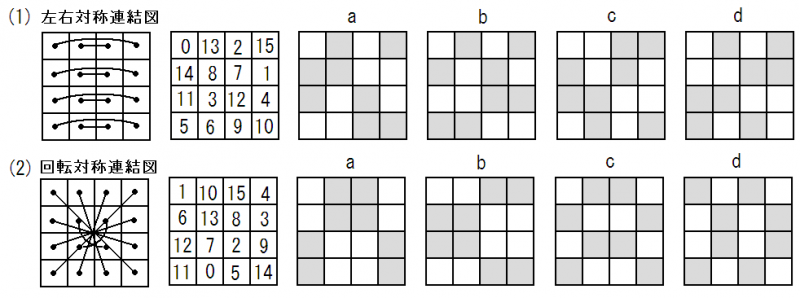
(1)左右対称の位置にある2つの数字の和は常に15になる.
(2)回転対称(2回対称あるいは点対称)の位置にある2つの数字の和は常に15になる.
このために右半分(あるいは左半分)を知れば,全部の数の配置がわかります.つまり,相手の意中の数がマスクに隠されて見えない場合は,その数との和が15となる数の方が見えているのです.
さて,0~15の数を2進数で表すと次の表のようになります.下図をご覧ください.a,b,c,dはそれぞれ2^3,2^2,2^1,2^0の桁に相当します.
2進数表示で3桁目を表すマスクカードがa,2桁目を表すマスクカードがb,というように4枚のマスクカードができます.
それぞれの数の上に乗る4種類のマスクカードで,2進数表示の1のところに孔を開ける(逆に統一してもかまわないが)ことにします.
例えば,13に場合は,aとbとdのマスクカードに孔(網掛け部分)をあけ,cのマスクカードには孔はあけません.
以上で,仕掛けの準備ができました.
これで,質問を開始して,数字が見えるといったマスクカードはそのまま横に置き積み重ねていきます.
見えないといったマスクカードは
(1)の場合には裏返して重ね/(2)の場合は180°回転して重ねるのです.
結局,4枚のマスクカードを重ねたものは,
相手の心の中で思っている数字の位置に孔があいた状態になっているはずです.