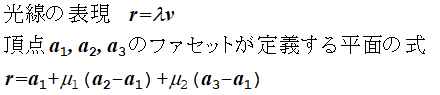Maths goes to the movies By Joan Lasenby
Submitted by plusadmin on March 1, 2007
http://www.plus.maths.org/issue42/features/lasenby/index.html
今回も,MMP,plusマガジン42号の筆者KTによる翻訳です(2回に分けて掲載).
数式が読みにくい場合は,数学月間の会http://sgk2005.saloon.jp,社会を支える数学科学でご覧ください(ホームページではTexを用いている).これは,2007年の数学月間懇話会で配布したものです.この後の13年でコンピュータビジョンの分野は非常に進化しましたが,原理の紹介には非常によく書かれたこのエッセイが役に立ちます.
------------------------------------------------------------------
ポップコーンは手に入れたか?よい席は選んだか?座り心地は良いか?それではタイトルロール....
■数学が誇らしげにプレゼント....
映画の中の信じられないほど真に迫ったコンピュータで作られた映像に皆な驚く.ジュラシック・パークの恐竜,ロード・オブ・ザ・リングズの不思議 ---- 特に,ガーラムの出演者 --- は,数学なしではできなかったということを知らない人が何と多いことか.どのようにして,これらの驚くべき映像が作られるのだろう?
コンピュータ・グラフィックス,コンピュータ・ビションは大きな課題だ.この記事では,完成作品に使われる数学のいくつかを簡単に概観する.最初に映画の世界を創造し,次にそれを生活へ持ち込もう.
■場面を作る
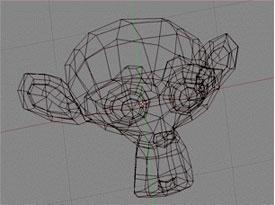
pblk0001.png
最初の対象物は,三角形のような単純多角形よりなる針金骨格として作られる.
コンピュータ生成映画を作る第一ステップは,物語中のキャラクターや,
それらが棲む世界を創造することだ.これら対象物のそれぞれは,
接続された多角形(通常は三角形)で構成された表面として作られる.
各三角形の頂点は, コンピュータメモリにストアされる.
どの三角形のどちらの面が,物体やキャラクターの外側であるかを知ることは重要だ.この情報は, ストアされている頂点の順番として,右ネジの規則に従い記号化される.これで,どちらが外か一意に決まる.
[頂点の順番に従い,三角形の周りを右手の指を人差し指,中指,..と回したとき]
諸君の親指が向いているのが三角形の外側だ.例でやってみよう.
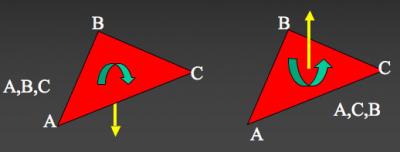
三角形(A,B,C)の外側方向(外側法線)は,三角形(A,C,B)の外側方向と反対であることがわかるだろう.
pblk0002.png
右ネジ規則で定義された(A,B,C)の外側法線は(A,C,B)とは反対方向
pblk0003.png
諸君の視点からファセット面までの光線を追跡しよう.光線は反射して光源を通過するか?
いまや対象物の表面は三角形の針金網だ.網のコンポーネントのそれぞれを彩色する準備ができた.
我々がモデル化している光景のライティングを,実際と同じにすることが重要である.これは光線追跡と呼ばれるプロセスを用いなされる.視点から物体へと遡り光線追跡し,反射させる.もし,目から出た光線がファセット面(針金網三角形の中の一つ)で反射され,光源を通過するなら,そのファセット面は光源に照らされ明るい色,もし,反射された光線が,光源を通過しないなら,そのファセット面は暗い色の影付をする.
光線を特定のファセット面まで追跡するには,表面を数学的に記述し,光線とファセット面の平面とが係わる幾何学方程式を解くことが必要になる.これはベクトルを用いなされる.光景の3次元座標系に,視点となる原点(0,0,0)を加える.
ベクトル v =( a, b, c ) は,原点から発し座標 a, b, c で終わる矢である.
例えば, v にスカラー2を乗ずるのは,規則 2v =2( a,b,c )=(2a, 2b, 2c ) に従い行う.
2v は v と同じ方向で2倍長い矢だ.
表現 λ v を見よう. λ は変数(言い換えれば,任意の実数).これはもはや,ある長さの矢ではない.長さが変数になったのだから.矢の方向だけを表している.別の言葉でいえば,この表現はベクトル v を含む直線を表す.
それは我々の視点からベクトル v の方向に発する光線を記述する.
三角形のファセット面で定義される平面は,3つの情報で表現される:
3頂点のうちの1つの位置頂点 $$a_{1}$$と, $$a_{1}$$から $$a_{2}$$へのベクトルと, $$a_{1}$$から $$a_{3}$$へのベクトルである.
下の囲みの中に,目とファセットで決定される面から発する一本の光線の方程式を与える.
光線がファセットをよぎるか否か,何処でよぎるかを知り,反射された光線の方程式を計算するには,
これらの2式を解かねばならぬ.
------------------------------------------
-------------------------------------------
(光線追跡の数学の詳細は,Turner Whittedの革新的な論文 ”影付け表示のための改良された照明モデル”,
Communication of the ACM,Vol.23,Isuue6に見ることができる.)
光線追跡は現実味ある光景を作り出すことができるが,たいへん遅い.
これはコンピュータが作る映画の製作には用いることができるが,コンピュータゲームのようにリアルタイムで照明を変化させることが必要な場合問題である.
影や火線束(コースティク)[収差による回り込みでできる光像],多重反射のような複雑な現象は,モデル化が困難で,動的あるいはもっと巧妙な数学的な手法,事前計算放射輝度伝搬(PRT)やラジオシティ(R)が使われる.
pblk0004.png
コンピュータゲームDOOM3,Neverwinter nights はダイナミックライティングが必要だ.
■必要なのは若干の想像力
光景,照明が出来てしまえば,監督が”アクション!”と叫び,キャラクターが動き出すのを待っばかりだ.いまや,数学がイメージに命を吹き込むのを確かめよう.
最も基本的な物体の動きの一つは,与えられた軸の回りの与えられた角度の回転である.
座標幾何学は,回転後の物体各点各点の位置を計算するツールを提供する.だがこれらのツールは効率的で高速であることが重要だ.これらのツールを見るにあたり,数学授業に一寸立ち寄って見る....
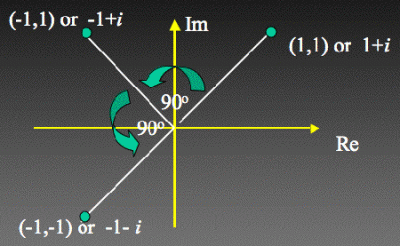
[この後,複素平面のこと,複素数に虚数iを乗じると反時計回りの90度回転になること,などの説明があるが略]
........
1806年にアマチュア数学者Jean Ribert Argandは複素数とiに幾何学的な解釈を与えた.複素数を乗ずることは,幾何学的には回転を表す.
■3Dへ
pblk0006.png
Broone橋にある記念プレート,Hamiltonが4元数を発明したときこの橋の下を散歩していた.
数学者William Rowan Hamilton卿はDublinのTrinityCollegeの最も著名な子であろう.
彼は最後の20年,複素数が2次元の回転を表すのと同様な,
3次元の回転の表現を捜し求め,人生の最後にHamiltonは,4元数という答えを見出した.
⇒次号に続く