球面正12面体の見える万華鏡をつくろう

いろいろな多面体の見える万華鏡（立体万華鏡と呼びましょう）を作ります．アルミ板やプラスチックの鏡は像がきれいに映りますが，ミラー紙(厚手0.25ｍｍくらい）を用いても，ここで取り上げているような立体万華鏡は良好に作れますので，チャレンジしてみてください．

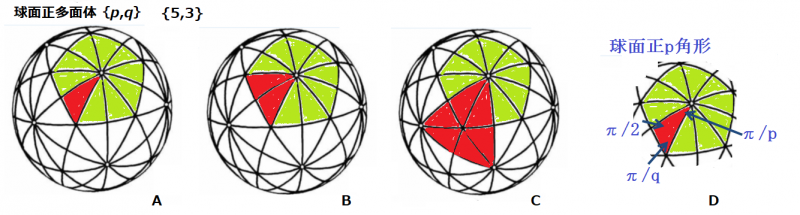
球面正多面体は，アラブの数学者，アブル・ワーファ（1000頃）に始まります．球面正多面体｛p,q｝は，球面正p角形が，頂点でq個集まっているもので，球面正p角形の１つの内角は2π/qです（図D）．
そして，球面p-多角形の辺はすべて大円であることに注意しましょう．

ここで具体的に取り上げるのは，正12面体に相当する球面正12面体＝球面｛5,3｝多面体です．

メビウスは多面体万華鏡を発明します（1850）が，これは，球面p-多角形を，2p個の球面直角３角形に分割することを使います（図A）．
分割された3角形の角度は，π/p，π/q，π/2，このような直角3角形を(p,q,2)と記述します．
万華鏡は，３角形（赤く塗った）の各辺となる大円を鏡にすると得られます．
（A）メビウス万華鏡になり，正5角形の面を10個の直角3角形に分割しています．
（B）正5角形の面を5個の2等辺3角形に分割しています．Bには，Aに存在した鏡映対称面が１つ消えています．
（C）赤く塗った正3角形の周囲の辺の大円を鏡に置き換えて万華鏡を作れば，正20面体の映像が見えます．

では，AとBを作ってみましょう：展開図は，前号の［正12面体の見える万華鏡を作ろう］に掲載してあります．

A(左写真)　　　　　　　　　B(右写真)

p.132～p.133　美しい幾何学より