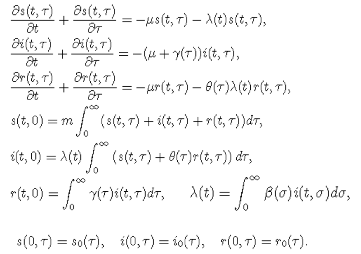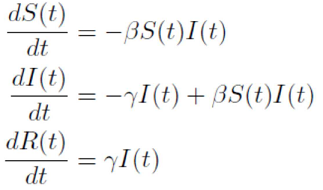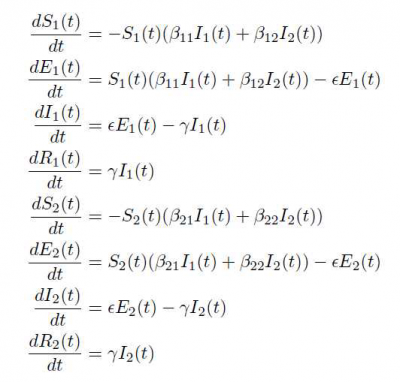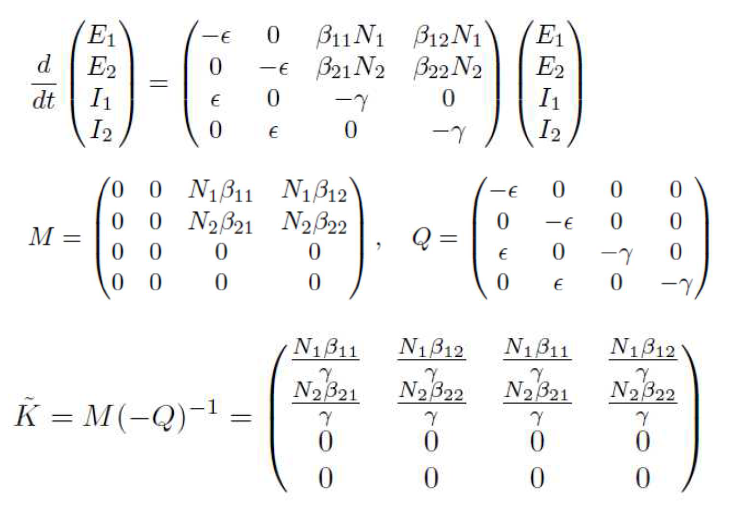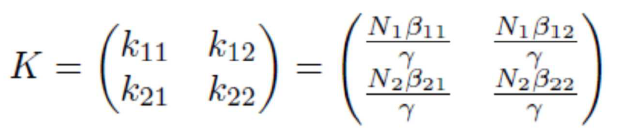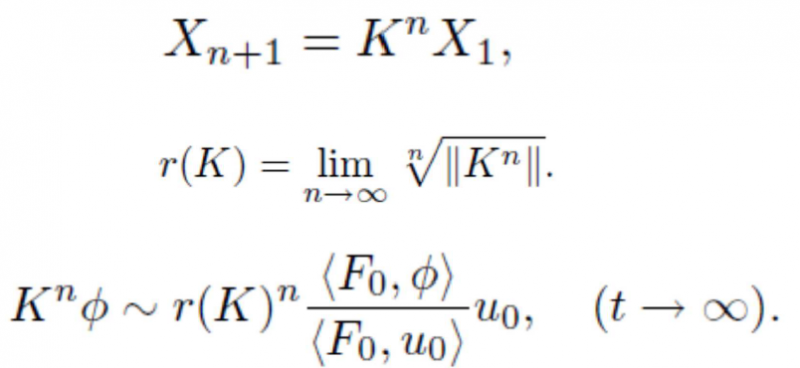数学月間懇話会(第16回),第3日目(2020.7.29)にZOOMにて表題の講演がありました.
■感染症の流行-現代社会最大のリスク要因
>1918年のパンデミックインフルエンザ(スペイン風邪)は4000万以上の死者,日本で
も40万程度の死者と言われる.
>2015年のHIV感染者は3670万、新規感染者210万、エイズによる死者110万
>マラリアは、全世界で年間に3億~5億人の患者、150万人~270万人の死者(90%はア
フリカ熱帯地方)
●新興感染症(SARS,BSE(vCJD),高病原性鳥インフルエンザ, Ebolaなど)、
再興感染症(結核、性的感染症、薬剤耐性の進化etc.)などによって、感染症撲滅に
関する1980年代までの楽観論は消滅。
人口増加、都市集中、環境破壊などによって、感染症流行リスクはますます増大.
●COVID-19は?
■モデリング
人口をSusceptible, Exposed, Infective, Recovered等の部分人口にわけて相互作用をモデル化する
介入(ワクチン接種、隔離、接触制限など)によって,「感染性」人口を絶滅(感染源にならないようにする)
Kermack and McKendrick I (1927)
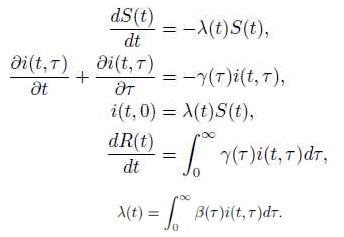
ケルマックーマッケンドリックのエンデミックモデルは
偏微分方程式の境界値問題として定式化される(Inaba 2001, 2016)
■基本再生産数R0(R-naught)
なんらかの病原体(ウイルスや細菌など)に対してすべてが感受性
(susceptible)を有する個体からなるホスト(宿主)人口(個体群)集団に
おいて典型的な1人の感染者が、その全感染期間において再生産する2
次感染者の期待数を基本再生産数(basic reproduction number)とよび、
R0で表す.
感染人口を世代毎にみて、1次(初期)感染者(primary cases)、2次感染者
(secondary cases)、3次感染者等を継続的に考えた場合、R0は等比級数
的に変化する各世代の感染者サイズの公比である。
Diekmann, Heesterbeek & Metzによって1990年に数学的な定義が確立.
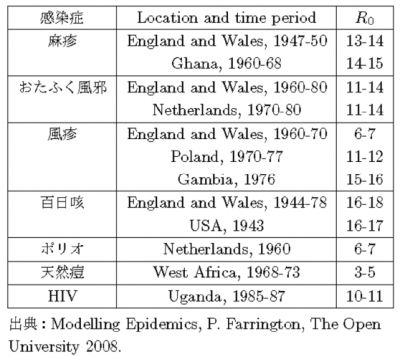
R0の推定値例
現在では,従来考えられたよりも数字の分散はずっとおおきく,桁違いの数字まで観測される.
生物的にきまる感染確率・感染性期間と環境によって決まる接触頻度の積なので,
数学的定義はともかく,実際の流行への応用に際して,非常に解釈が難しい数字でもある.
■例
S:感受性人口、I:感染(性)人口、R:回復・隔離人口、
β: 伝達係数、γ: 回復・隔離率(1/γ=平均感染性期間)
侵入のモデル(線形化)
• 感染人口の初期成長(マルサス法則):
• 感染人口の初期成長率:
• 世代時間T(二次感染までの平均待機時間):
• 侵入条件(invasion threshold)
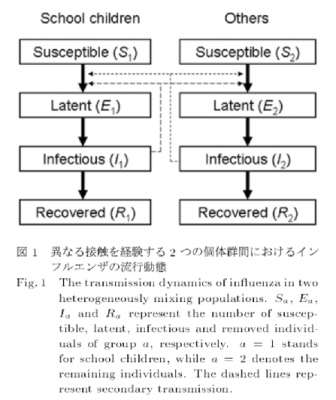
■多状態モデルの例題ー2状態SEIRモデル
ホスト人口を、明らかに最終規模の異なる二つの集団(学童とそれ以外)
に分割してSEIRモデルを適用(インフルエンザの場合)
状態1=学童、
状態2=それ以外
潜伏期間、感染性期間は同一と仮定
多状態SEIRモデル
-----