ガーキンの全貌.平面パネルが曲面を近似していることに注意.映像 © Foster + Partners
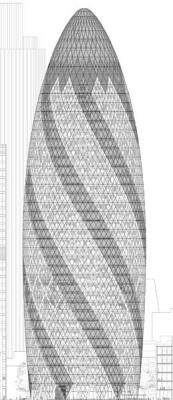
ガーキンやロンドンシティホールや,他の多くのFoster+パートナーズの作品がたいへんモダーンに見えるのは,外側が曲面であるためです. しかし,曲面を作るのはとても困難で,建設費が高くなります.そこに幾何学者のチャレンジがあります:単純な形から作る一番良い方法は何か?
「これが我々の主たるチャレンジの一つだ」とDe Kestelier(SMGメンバーの一人)は語ります.
「我々のプロジェクトの実に99%は,いかなる曲面も使っていない.
例えばガーキン,1種類の曲面パネルはトップにあるレンズのみだ.
建物が曲面という印象は,多数の多角形の平面パネルで曲面を近似的に作ることで生じる.パネルが多いほど錯視も真実味をおびる」
複雑な表面を記述するこのような平面パネル解を見いだすのが,SMGの仕事です.De Kestelier が説明するように,幾何学[その形]は,しばしば経済により決定される:「我々は矩形に近いパネルを使う傾向がある.なぜならそれはいっそう経済的であるからだ.資材をカットするとき安くなる」
三角形では,多くの材料ロスがあるが,矩形に近いとロスが少ない.
また,矩形に近いと構造が少ないので,視覚的にもさらによい.これは,
表面が完全に矩形から成り立っているロンドンシティホールで実証されました.
実際,ロンドンシテイホールは,理想的な幾何学形と建設容易さのバランスがよく取れている例です: 扱い難い丸い形はスライスに切ることにし,スライスの一つ一つは,僅かに傾いたコーンで容易に数学的に記述できて平面パネルでの近似も容易です.
■合理的な設計
数学的な方程式で記述されるコーンのスライス,トーラス,球などの表面は,しばしば,SMGデザインの基礎となります. これらを,バーチャル・モデルの創造に使うときに,数学的に生成される表面はコンピュータ上で容易に表現できるのでたいへん利点があります.
たくさんの個別座標を蓄え記述する構造ではなく,方程式を蓄えるだけでよい.表面の正確な形は方程式のパラメータを変じて制御できます(例として下図を見よ).[記述に必要なメモリが圧倒的に少なくなる]
平面解はやはり比較的容易に設計できる:ソフトウェアはオリジナルの表面のノードポイント集合に直線を引くようにする.
http://plus.maths.org/issue42/features/foster/surfaces_web.jpg
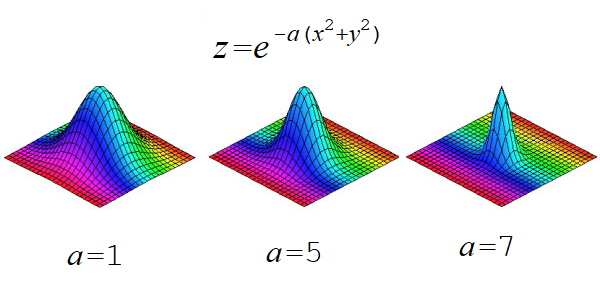
これらの表面は,関数z=e^-a(x^2-y^2) のグラフである.ここで,
3次元座標系は,x,y,z(上向き)軸であり, a は表面の形を決める.
第一の表面はa=1 ,第二の表面はa=5 ,第三の表面はa=7 .
数学的に定義された要素の集合からなる複雑な構造を考えるのは,
バーチャル世界では有用ではない:建物モデルから実際の建設手順のガイド作りを支援する合理化のこのプロセスは,もう一つの SMG の仕事の重要な部分だ.
同様に,数学的な完全性は,実用性のために道を譲る必要がある:「2~3週間前のことだが,楕円の一部である壁のプランのことで私のところに来た建築家がいる」とDe Kestelierは語った・・・
もちろん楕円は数学的には描くのは易しいのだが,それをさらに合理化することを望むのはなぜか?
私は楕円の弧を3つの円弧に合理化することを決めた.理由は,壁の建設でコンクリート壁用の型が要るためだ.これは全体の形を建設するのに多くの型パネルを使ってなされる.もし諸君が正確に楕円にしたいなら,すべての型パネルは異なっていなければならない:楕円の周囲を進むと,楕円の曲率はたえず変化しつづけるのだから. もし楕円をやめて3つの弧にするなら,諸君が必要とするのは,3セットのパネルだけで,各セットのパネルは同じである.
これならずっと簡単になる.「 数学者に理想的なものは,建築家に理想的であるとは限らない」
http://plus.maths.org/issue42/features/foster/museum.jpg
英国博物館の屋根.設計Foster+パートナー
■博才の人
SMG が,建物の外見と気流・音響のような物理現象の双方をモデル化するには,コンピュータプログラミングを使う.幾何学[形]の理解は,デザインと建設プロセスに直結する.
「建築家でなく数理科学の専門家なのか? SMGメンバーの8人中7人が,プロの建築家だが,専門的知識は,複雑な幾何学,環境シミュレーションからパラメトリックなデザイン,コンピュータ・プログラミングにまで及んでいる.グループの8番目のメンバーはエンジニアで,主プログラマーである.
こみいった数学に基づき,物理的特徴をモデリングするとなれば,
チームはしばしば専門コンサルタントを使う.チーム内で予備的な解析を行ない,もしさらに知りたければ別の解析を行う.「我々は,専門コンサルタントとデザイナー間の接点となる」とPetersは説明する.
純粋数学,幾何学は如何? どれぐらい複雑なのか?
「オフィスに1Aレベルの本がある」と,De Kestelierは語る.結局のところ,それはすべて建設可能な構造を作ることに関わり,古典幾何学を越えるものはここでは用いない.
SMG の大部分の活動には数学が付随しているのだが,彼らのデザインとは,
仕事に対して制限を与えるものであるとPetersとDe Kestlierは主張する.
「悟るべき重要なことは,我々はアーキテクチャで働くプログラマーではなく,プログラミングをするアーキテクトだということだ」とDe Kestlierは語った.
Petersも同意する:「我々の主な仕事はモデリングではない.
プロジェクトのパラメータは何かを理解し,噛み砕き定義できる規則にする.我々は,何処に適応性があり何処に制限があるかを理解できるようにする」 制限の最適化と建設可能な物体の創造.もちろん,建築家はいつもそうしてきたし,PetersとDe Kesteierも建築の仕事は本質的には変わっていないと思っている.
現代のデジタルツールにより,今日の建築家は,過去の世代には夢であったデザインオプションの領域も探索できるようになっただけだ.
形と模様,科学とコンピュータの言語として,これらのツールを自由に使えるようにしたのは数学だ.数学は確かにその料金を取り戻している.(訳:KT)
-----------------
◆編集後記
ガーキンとロンドンシティホールを設計したFoster+Partnersについての記事は,Marianne Freiberger(プラスマガジン編集者)による,MMP, plusマガジンVol.42の記事を,筆者(KT)が翻訳し若干編集しました.
原著エッセイを,3つに分割して(その3)に当たるものです.
Perfect buildings: the maths of modern architecture
By Marianne Freiberger
http://plus.maths.org/issue42/features/foster/xavier_brady.jpg

Xavier(左)とBrady(右)はFoster+Partnersのモデリング専門家メンバーである.プラス編集者は,ロンドンの数学と芸術ブリッジ会議(2006年)で,二人に出会った.ブリッジ会議の詳細はウエブサイトにある.
Marianne Freiberger(プラス編集者)
◆ところで,ガーキンに良く似た超高層ビルが新宿にあります.2008年に完成した東京モード学園が入っているコクーンタワーです.コクーンとは繭のことですがどちらかというとセミに似ているビルです.設計は丹下都市建築設計です.新宿で大変目立つビルです.