エッシャーの「極限としての円」

■エッシャーのトリック（引用先：コクセター論文）
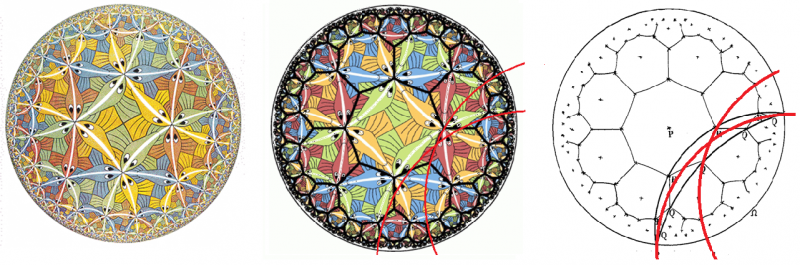
M.C.エッシャーの「極限としての円」Circle limit IIIを鑑賞しましょう（図左）．
この円盤内は双曲幾何の世界（ポアンカレの円盤モデル）です．
この円盤内を旅する人は，円の縁（世界の果て）に近づくほど時間がかかる．つまり，［世界の果てに到達するには無限の時間がかかる］ようになっています．
この世界で定義される直線（最短時間で移動できる経路）は，円盤世界の縁で直交する円弧です．
エッシャー作品（図（左））の円盤は，魚の流れを示す白い線で分割された双曲面の[4,3,4,3,4,3]分割のようにも見えますが，実は，図（中）に示すような，黒い線で分割した{8,3}正則分割です．
白い線は，双曲幾何の円盤世界の縁に80°で交差し，直線ではないのです．
図（中）の正8角形の黒い線がこの円盤世界の直線であることは，図（中）に書き込んだ赤い円弧（いずれも円盤縁で直交する円弧）を見れば理解できるでしょう．

双曲平面の正８角形タイルは，双曲平面の直線（円盤の縁で直交する円弧）で囲まれています．
タイルの大きさは円盤の縁に行くほど小さく見えますが，円盤内は無限に広い双曲幾何平面なのですべて同じ大きさです．
１つのタイルの中には4匹の魚がおり中心に4回軸があります．
正8角形の頂点には3回軸があり，魚の白い流れは3回軸の場所に集まっています．
エッシャーは｛8,3｝分割に用いる直線をわざと隠し，白い流れが分割であるようなトリックを見せます．もちろん，白い流れの円弧（直線ではない）に関して鏡映対称はありません．

参照：「美しい幾何学」p.142,143