2017年の数学月間懇話会(第13回)の講演の一つとして,ブラックホールの形を見る(池田思朗)をとりあげました.ブラックホールはなんでも引っ張り込み光も脱出できません.しかし,ブラックホールの穴に荷電粒子が引き込まれるときに電波やX線が放出されるので,ブラックホールの形は,この放出される電波を観測(地球上の6地点の電波望遠鏡を結んで電波干渉計を作り,電波の強度とその位相を観測)して,それらのデータをFourier変換すると形が見えるはずです.しかし,Fourier変換に用いる観測データは,地球が宇宙空間で旅した範囲の観測点で得られるのは圧倒的に限られたデータしかありません.
ブラックホールの穴画像を$$x$$,観測されたデータを$$y$$とすると,$$y=Ax$$
(行列$$A$$や,形式的な逆行列$$A^{-1}$$は線形演算子で,Fourier変換やその逆変換のことです).
行列Aが正則ならば逆行列を両辺に左から乗じて,$$x=A^{-1}y$$と簡単に解くことができるのですが,$$y$$の次元$$N$$は非常に小さく,$$x$$の次元$$M$$は非常に大きい(行列$$A$$は$$N$$x$$M$$行列でランク落ち)ために解けません.多数($$M$$個)の未知数のある$$x$$を解くのに,式の数($$N$$個)が少ないので,不定解になります.もし,解$$x$$にたくさんの0要素(スパース)があるとしランクを下げれば,一意解を持ちます.なぜこのようなスパースな解が合理的なのかは難しいのですが,我々のまわりの画像は統計的にスパースなようです.この方法は,LASSO(Least Absolute Shrinkage and Selection Operator)といいます.数学的には,$$x$$がスパースであるという条件を,$$Σ|x_{i}|$$が最小という条件にして,最小2乗法$$||y-Ax||^{2}$$ を解き,少ない観測値$$y$$から$$x$$を求めます.このための数学には,ラグランジュの未定乗数法が適用できます.
■圧縮センシング
このような手法は,医学画像(MRIなど)解析で用いられており,高速で高解像度の画像が測定できる圧縮センシングとして役立っています.得られる画像の解像度を上げるには,観測空間でも細かくたくさんのデータを収集し,それらを用いてFourier変換を行うのが正攻法です.これは情報理論でシャノンのサンプリング定理(注)と呼ばれるものであります.
しかし,実際には画像内で急峻な変化がある場所は少なく大体がだらだら変わっています.そのような性質のある実際画像では,観測空間内を細かい分解能で測定するのは時間がかかり過ぎてもったいない.観測空間の少数の点だけのデータで十分なのです(この考え方はjpgなどの画像圧縮と同じ).得られる画像は至る所0(スパース)という仮定は,大胆であるが良い結果をもたらします.
観測空間のサンプリングをナイキスト・レート(注)より細かく行う場合はオーバーサンプリング,ナイキスト・レートより粗い場合はアンダーサンプリングと呼ばれますが,画像がスパースという条件があれば,アンダーサンプリングのデーター集合を用いて解像度の高い原画像が再現できるのです. 解のスパース性を利用するこの手法は,医学画像(MRIなど)の撮影で利用でき,高解像度の画像を短時間で得られるようになりました.
ーーーーーーーーーーーーーーーーーーーーーー
(注)シャノンのサンプリング定理(1949年)
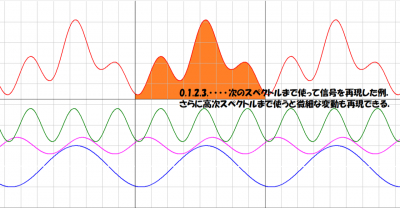
アナログ信号をあるサンプリング・レートでデジタル化すると,元のアナログ信号に含まれる周波数成分のうち,サンプリング周波数(ナイキスト間隔とも呼ばれます)の1/2の周波数成分までが再現できます.ナイキストは,サンプリング定理を1928年に予想していました(シャノンの証明が広く知られています).
デジタル音源のサンプリング周波数は44.1kHzが使われていますが,この周波数でサンプリングすれば,人間の耳が聞き分ける高音限界といわれる20kHzの音まで十分に再現できるからです.
ーーーーーーーーーーーーーーーーーーーーーー