ナポレオンが発見したといわれるナポレオンの定理とは次のようなものです.
ーーーーーーーーーーーーーーーーーーーーーーーーー
ナポレオンの定理
任意の⊿ABCの各辺上に正3角形を作図し,それら3つの正3角形の重心をD,E,Fとする.D,E,Fを結んでできる⊿DEFは正3角形である.
ーーーーーーーーーーーーーーーーーーーーーーーーー
なかなか美しい形の定理ではありませんか,ナポオンの名を冠するのにふさわしい定理だと思います.ただし,ナポレオンが発見したかどうかは記録がなくわかりません.
ナポレオン (1769 -1821) は数学好きです.
陸軍幼年学校で,代数,三角法,幾何などを勉強し,数学で抜群の成績をおさめ,1784年にパリの陸軍士官学校に入学.数学が役に立つ砲兵科へと進みます.騎兵科,歩兵科でなく砲兵科に進んだのも戦術の時代の流れを見据えての決断でしょう.砲兵司令官,将軍,皇帝になりました.この時代にフランスには多くの数学者がいました.ラプラス,モンジュ,フーリエなどが近くにおり,エジプト遠征 (1798 年) にはモンジュやフーリエが同行しました.
ナポレオンは数学が大好き,このような幾何問題を考えるのが楽しみで,きっと定理を発見したのだと私は想像します.
証明
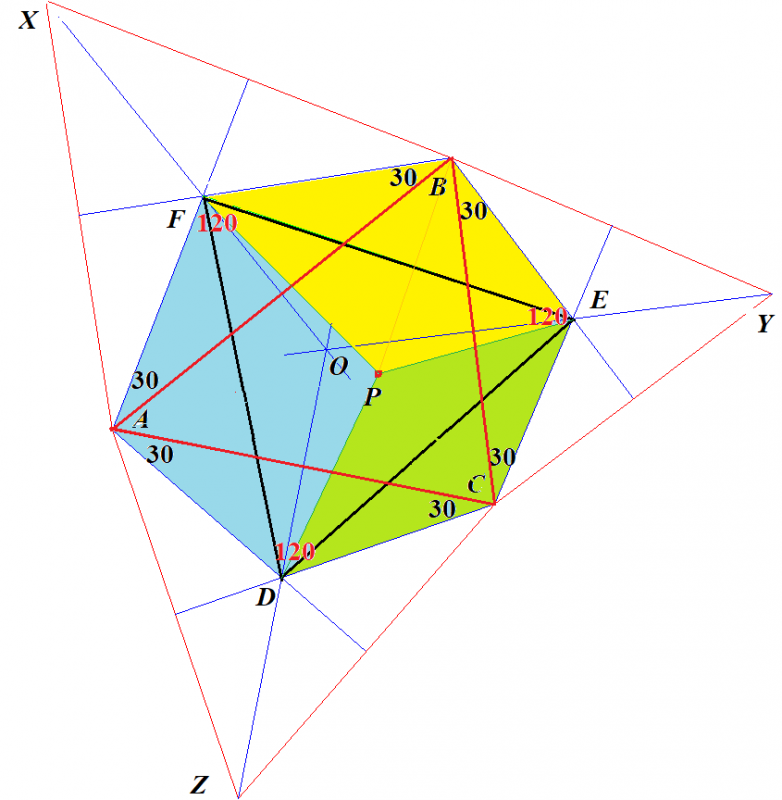
与えられた任意の3角形を⊿ABCとします.
その各辺上に作図した正3角形のそれぞれの重心がD,E,Fです.
点Oは⊿ABCの垂心(⊿ABCのそれぞれの辺の垂直2等分線が交差する点)で,点D,E,Fは,この垂直2等分線上にあります.
色々な角の角度は図中に記入してあります.我々が証明すべきことは,⊿DEFが正3角形であることで,例えば,∠DFE=60を証明すれば済みます.考えてみてください.
ヒントは,∠BFE=∠BXC と ∠AFD=∠AXC を証明することです.
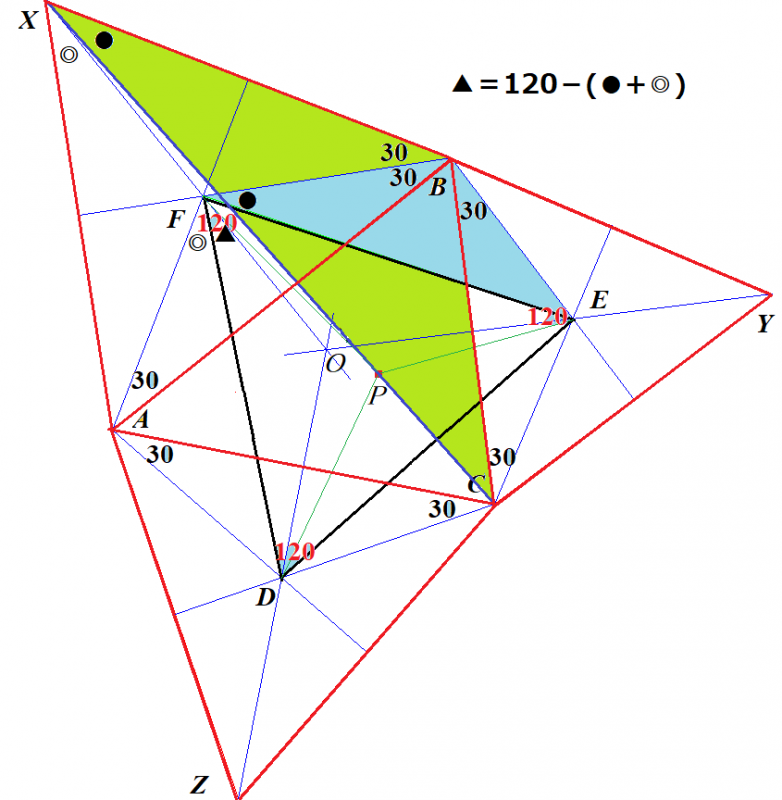
正3角形であるための必要十分条件は「3つの内角すべて(すくなくとも2つの内角)60°」です.
図形の対称性から,内角の1つが60°であることを証明すれば済みます.
これは,補助線1本引けば自明です.三角関数を使って計算で証明する方法もありますが,補助線1本で自明になるのが幾何の醍醐味です.
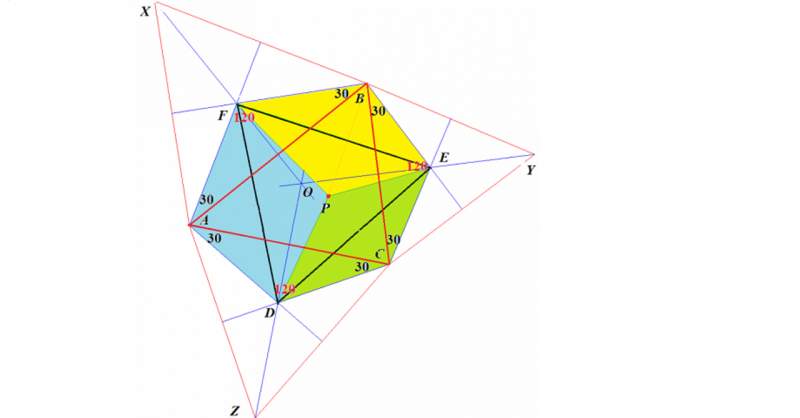
■さて,ここに出てきた6辺形には面白い性質があるのを見つけました.
この6辺形の中にある正3角形の中に点Pを中心になるように,正3角形の外の6辺形の部分を折り込むことができます.