■モワレMoire:The superposition of two regular nets produces a secondary enlarged net of the same shape.
2枚のグレーチング(格子模様)を重ねたとき,グレーチングの拡大像らしきものを見たことはありますか?
これはモワレ現象の一種です.決して格子の穴の一つが拡大されて見えるわけではありません.
2枚の全く同じグレーチング(格子模様)を重ねたとき,両者の方位が互いに少し傾いているので,モワレ縞を生じます.
これは,2枚のグレーチング模様が運よく重なった場所の周囲はよく光を透過するので明るく見え,模様の重なりがずれている場所の周囲は,透過光が少なく暗く見えることによります.重なる場所の出現は周期的ですから,重ね合わせ像のコントラストには周期的な分布ができます(ビート,うなりのようなものです).見かけの拡大率は,重ねたグレーチング間の傾きがわずかだと高倍率,傾きが大きいと低倍率に見えます.
さてこの3枚の写真のそれぞれは,全く同じ2枚のグレーチングが平行移動(傾きはなく)して重なっている状況です.これらの写真を見ると,やはり2次元的なビート・パターンが生じているのですが,全く同じグレーチングが平行にずれても,新しいビート・パターンは生じないはずです.ではなぜこのようなビート・パターンが生じたのでしょうか?
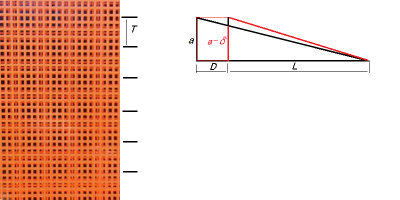
それは,2枚のグレーチングの間にスペース $$D$$ があるために,観測者から視差(パララックス)があり,前方のグレーチングよりも後方のグレーチングを小さく見込むためです.これは,わずかに寸法の違うグレーチングを重ねたのと同じ現象なので,このためにビート・パターンが生じているのです.
■考察
では,計算してみましょう:ノギスの副尺の原理を思い浮かべると良いでしょう.
本当のグレーチングの格子のサイズ $$a$$
2枚のグレーチングの間隔 $$D$$
視点から表面のグレーチングまでの距離 $$L$$
後ろのグレーチングの縮小割合 $$δ/a≡q<1$$
として,生じるビートの周期 $$T$$ を求めて見ましょう.
$$a/(D+L)=(a-δ)/L$$ より $$δ/a=D/(D+L)$$
$$T≡n・a=(n+1)(a-δ)$$より $$δ/a=a/(T+a)$$ ⇒ $$T=a(1/q-1)$$ ← $$D, L$$ を消去した
あるいは, $$T=a(L/D)$$ ← $$q$$ を消去した
さて,この例で生じた新しいビートの周期は, $$T=5a$$ のように観測されます.
従って,$$L/D=5$$ が得られます.あるいは,$$1/q=6$$,つまり $$δ/a=1/6$$ です.
2枚の同一なグレーチングの間隔$$D$$で重ねたとき生じるビートが,もとのグレーチングのn倍に見えたら,観測点から表面のグレーチングまでの距離は$$L=n・D$$です.これは間隔$$D$$が既知の時,距離$$L$$ を計測する道具に応用できます.
ただし,$$n=1,(T=a)$$はモアレとは言いません.$$a/2$$周期の均一なコントラスト分布です.