■正5角形の性質
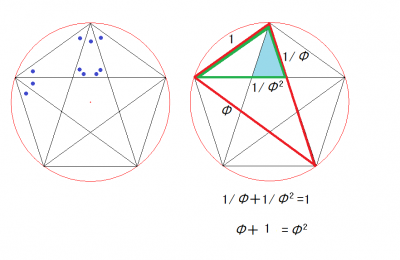
正5角形の中に相似な2等辺3角形(頂角36°)が次々に組み込まれていく様子を見てください.赤い2等辺3角形→緑の2等辺3角形→青い2等辺3角形の順です.2等辺3角形の辺の比率は,いつもΦ:1で,Φは正5角形の対角線(星形の辺),1は正5角形の1辺です.このとき成立する方程式,Φ2-Φー1=0を解いて(Φ>1をとる),Φ=(1+√5)/2=1.6180・・が得られます.Φは黄金比の値です.
■正5角形の実用作図法
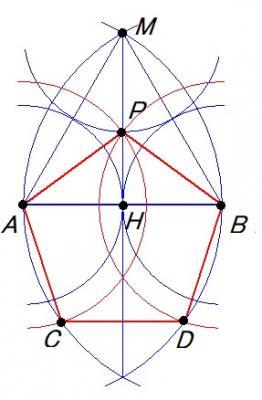
この作図はつぎの式が成り立ちます.AH=HB=1/2,MH=√3/2 であるので,PH=(√3ー1)/2,従ってPB=(√[(√3-1)2+1])/2=(√[5-2√3])/2
AB/PB=2√(65-26√3)/13=1.6138・・・
この作図法は,イスラームのタイル作図で便利ですが,厳密な正5角形ではありません.しかし,誤差は0.26%なので実用上問題ない恐るべき精度です.
■厳密な正5角形の作図
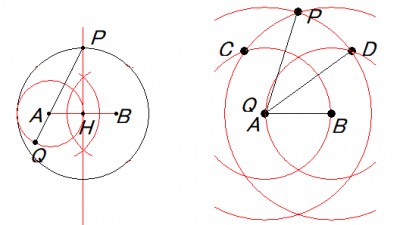
AB=1,AH=1/2,PH=1 ですので,AP=(√[1+22])/2=√5/2
従って,QP=(1+√5)/2=Φ
この作図で得られるのは厳密に正5角形であることが証明されました.
■折り紙で作る正5角形(1)の精度
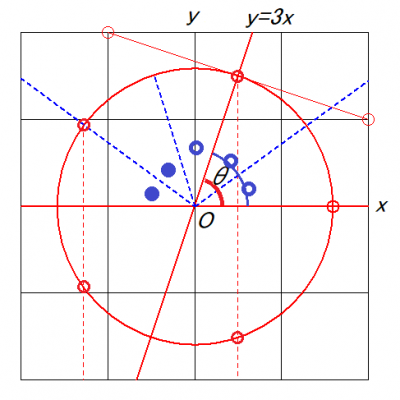
この図は折り紙で正5角形を作る原理を示しました.y=3xの直線とx軸のなす角θを求めると,θ=arctan3=71.5651・・° となりますが,正5角形では72°になるべきです.この誤差は.0.6%ですのでかなり良い精度と言えましょう.他の角度は,72.1087(0.2%),72.6524(0.9%)程度です.(カッコ内は誤差)
■折り紙で作る正5角形(2)の精度
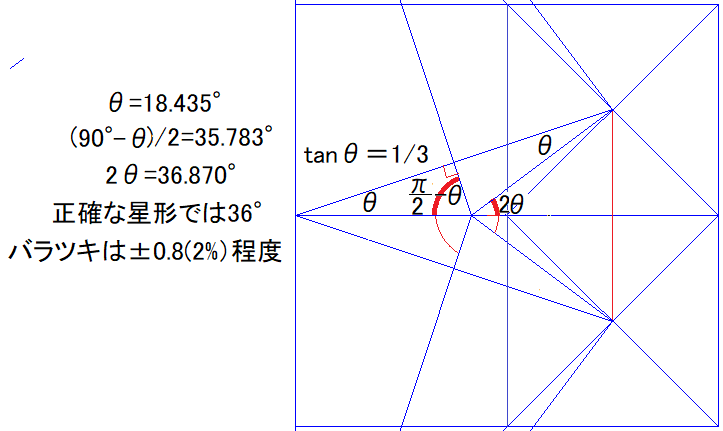
折り紙の一太刀切で大変作り易い星型です.この原理は以下の図を見てください.正5角形(星型)の一辺の中心角は360°/5=72°ですから,一太刀切りに対応する中心角は36°です.
以下の図を見ると,一太刀切りの中心角は,35.783°(36°からのハズレは-0.6%)to,36.870°(+2.4%)に収まっています.