クバンチクの問題４

ロビンソンは，円形の無人島に流れ着きました．ロビンソンが海岸の小屋を出て，西に3 km，南に4 km移動した後，彼は海岸に出ました（その日は小屋に戻りました．）．翌日は，ロビンソンは小屋を出て南西に１0 km行くと海岸に出ました．1日後，ロビンソンは海岸沿いに島を一周することにしました．彼が歩く一周の距離はどのくらいありますか？

A.約16 km
B.約31 km
C.約63 km
D.約113 km
E.正解は異なります。

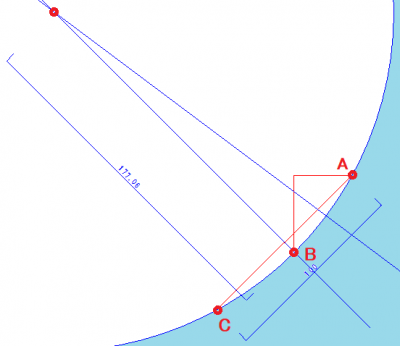
■解答です．図を描いて考えましょう．

最初の日は，AからBに行きます．（その日はまたAに戻ります）次の日は，AからCに行きます．A,B,Cは海岸にある点ですから，この3点を通る円の中心を求めれば円の半径rがわかり，島の全周囲は2πrとなります．

解答は，Dです．

この問題で紛らわしいのは，最初の日はAの小屋にもどると書いていないところです．（小屋にもどる）というのは私が補足しました．次の日の出発点をBとすると，非常に大きな円になります．半径51kmで全円周320kmになります．無人島の探検なのだから，小屋はAしかないのでしょうが，紛らわしいのではっきり出発点に戻ることを書いてほしかったです．

この問題は作図で解くのが良いと思いますが，座標を用いて計算で解くこともできます．西，南の方向を＋にした座標で書くと，A(0,0),B(3,4),C(10/√2,10/√2）で，円の中心(a,b)，半径rの円の方程式(x-a)^2+(y-b)^2=r^2

に，A,B,Cの座標を入れた3つの式を連立させて解き，半径rを知ればよいのです．