フィボナッチ数はいろいろな所に現れます.この記事はThomas Koshyの著書からの引用で,2018.09.25発行のメルマガSGK通信No.234のリメイクです.
━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 [2018.09.25] No.234
<<数学と社会の架け橋=数学月間>>
━━━━━━━━━━━━━━━━━━━━
フィボナッチ数列は次のように定義されます.
F(n)=F(n-1)+F(n-2).F(1)=1,F(2)=1として数列を作ると
1,1,2,3,5,8,13,21,.......の数列が得られます.
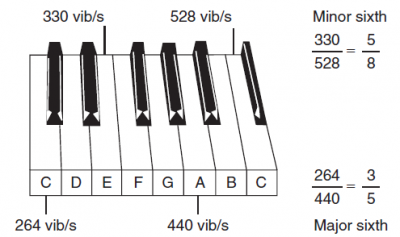
ピアノの鍵盤は,フィボナッチ数と音楽のつながりの可視化の良い例です.
鍵盤上で1オクターブとは,2音の間の音程で高音の周波数が低音の2倍になっていることです.鍵盤でいうと,1オクターブは,5つの黒鍵と8つの白鍵,合わせて13の鍵で構成されます(図).この5つの黒鍵は2つのグループをなしています;一方は2鍵よりなるグループ,他方は3鍵よりなるグループ.
1オクターブに入る13の音は,西洋音楽で最も一般的な音階であるクロマチック音階(半音階)を作ります.クロマチック音階に先行して,2つの他の音階;5音からなるペンタトニック音階と8音からなるダイアトニック音階がありました. お馴染みの"Mary had a Little Lamb” と “Amazing Grace” は,ペンタトニック音階を使い演奏でき,また, “Row, Row, Row Your Boat” のメロディーはダイアトニック音階を使い演奏できます.
長6度と短6度(6つ離れた音,および,5+1/2離れた音)は,耳を最も喜ばす2つの音程(和音)です.長6度は,例えば,音CとAから成る:それぞれの音は,1秒当たり264と440の振動数で(図),264/440 = 3/5はフィボナッチ比であるに注目しましよう.
短6度は,例えば,1秒当たりの振動数330と528の音であるEとCから構成され,それらの比もフィボナッチ比です: 330/528 = 5/8.
[訳注)自音の音程は1度という.1オクターブの音程は8度である.]


