コーシー (1789-1857)、リーマン (1826-1866)
これも19世紀の数学で重要な発見の一つです.「数学が社会(科学技術も含まれる)とどのように係わるかを知る」のが私たちの目的で,数学の勉強会とは別物です.そのような視点で見ても,複素関数論は19世紀に確立した重要な数学分野で,広い応用をもちます.そこで,この数学概念の意義を理解できることを目指します.
私たちの使う関数論は19世紀の数学で確立しました.先に,Fourierフーリエ級数(変換),Laplaceラプラス変換を取り上げましたが,もう少しだけ複素関数に言及する必要があります.今回は,コーシー-リーマンの方程式を取り上げます.
複素平面($$x$$軸が実数,$$y$$軸が虚数)に定義域$$D$$をもつ複素関数$$f(z)$$を考えましょう.この関数は領域$$D$$で正則(微分可能)であるとします.微分可能な関数ですから,この領域$$D$$で連続であることはいうまでもありません.
ある点$$z∈D$$での微分は,$$x$$軸に沿って($$x$$で偏微分)行う微分係数と,$$y$$軸に沿って($$y$$で偏微分)行う微分係数がありますが,複素関数$$f(z)$$が正則であるとすると,どちらの微分係数も一致し,点$$z$$での微分係数は確定しなければなりません.
関数$$f(z)$$が$$D$$で正則とは,定義域$$D$$のすべての点$$z∈D$$で微分係数が確定する(微分可能)ことです.
関数$$f(z)$$に領域$$D$$での正則性を要請します.定義域内のすべての$$z=x+iy$$に対して,
$$\displaystyle \frac{df(z)}{dz}=\displaystyle \frac{ \partial u}{ \partial x}+i\displaystyle \frac{ \partial v}{ \partial x}=\displaystyle \frac{ \partial u}{ \partial (iy)}+i\displaystyle \frac{ \partial v}{ \partial (iy)}$$が成立します.$$x$$で偏微分しても,$$iy$$で偏微分しても等しい.
実部と虚部をそれぞれ等しいとおいて,
$$\displaystyle \frac{ \partial u}{ \partial x}=\displaystyle \frac{ \partial v}{ \partial y}, \displaystyle \frac{ \partial v}{ \partial x}=-\displaystyle \frac{ \partial u}{ \partial y}$$が得られます.これをコーシー-リーマンの方程式(条件)と言います.
逆に,コーシー-リーマンの方程式が成立するなら,複素関数f(z)は正則であることが証明できます.
従って,複素関数が正則であるための必要十分条件は,コーシー-リーマンの方程式が成立することです.
■閉曲線$$C$$とその内部で,$$f(x)$$が正則であれば,$$\displaystyle \int_{C}^{}f(z)dz=0$$ ←コーシーの積分定理
(コーシーの積分定理の証明)
$$\displaystyle \int_{C}^{}f(z)dz=\displaystyle \int_{C}^{}\left[ u(x,y)+iv(x,y) \right] \left( dx+idy \right) =\displaystyle \int_{C}^{}\left( udx-vdy \right) +i\displaystyle \int_{C}^{}\left( udy+vdx \right) =$$
$$ =\displaystyle \int_{D}^{}\left( \displaystyle \frac{ \partial v}{ \partial x}+\displaystyle \frac{ \partial u}{ \partial y} \right) dxdy+i\displaystyle \int_{D}^{}\left( \displaystyle \frac{ \partial u}{ \partial x}-\displaystyle \frac{ \partial v}{ \partial y} \right) dxdy=0 $$
(参考)
$$\displaystyle \int_{C}^{}\displaystyle \frac{f(z)}{z-z_{0 } }dz=f(z_{0})\displaystyle \int_{\mit\Gamma }^{}\displaystyle \frac{dz}{z-z_{0 } }=2\pi if(z_{0})$$
■正則な複素関数$$f(x,y)=u(x,y)+iv(x,y)$$はその実数部$$u(x,y)$$あるいは虚数部$$v(x,y)$$のどちらか一方を知れば他方は決まってしまう.
例えば,虚数部$$v(x,y)$$を知り,コーシー-リーマンの方程式を使うと,実数部$$u(x,y)$$を求めることができる.
例えば,以下のyoutube動画には,このような問題の演習があります.
■応用について
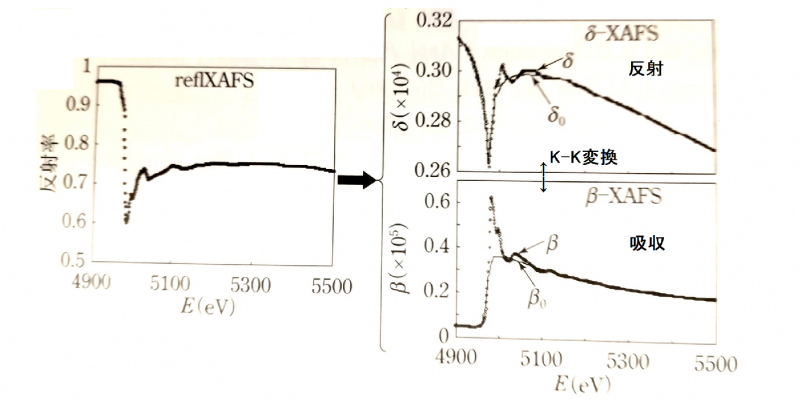
実数部を知って虚数部を求める例として,私のやった実験の話をします.
複素屈折率を $$ \tilde{n}(\omega )=n(\omega )+iK(\omega ) $$と書きます.$$ω$$は光の周波数で実数.複素屈折率$$ \tilde{n}(\omega ) $$は,複素数値をとり,実数部$$n(ω)$$と虚数部$$K(ω)$$があります.
実数部の$$n(ω)$$は反射率に,虚数部の$$K(ω)$$は吸収率に関係があります.
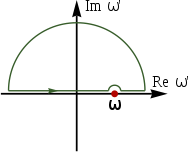
反射率を測定し$$n(ω)$$を知り,$$K(ω)$$を計算し吸収率を求めます.このとき,実数部$$n(ω)$$と虚数部$$K(ω)$$を結ぶのは,クラマース-クローニッヒ変換です.$$ω$$は複素数ではないので,コーシー-リーマンの方程式にははなりませんが,$$ \displaystyle \frac{\tilde{n}(\omega )}{z-\omega } $$は実軸より上側で正則($$ω$$は極)なので,コーシーの積分定理を使うと,クラマース-クローニッヒ変換を導くことができます.
$$0=\displaystyle \int_{}^{}\displaystyle \frac{n(z)}{z-\omega }dz+i\displaystyle \int_{}^{}\displaystyle \frac{K(z)}{z-\omega }dz=P\displaystyle \int_{- \infty }^{+ \infty }\displaystyle \frac{n(z)}{z-\omega }dz-i\pi n(\omega )+iP\displaystyle \int_{- \infty }^{+ \infty }\displaystyle \frac{K(z)}{z-\omega }dz+\pi K(\omega )$$
$$\left\{ \begin{array}{@{\,} c @{\, } }
-\displaystyle \frac{1}{\pi }\displaystyle \int_{- \infty }^{+ \infty }\displaystyle \frac{n(z)}{Z-\omega }=K(\omega ) \\[0mm]
\displaystyle \frac{1}{\pi }\displaystyle \int_{- \infty }^{+ \infty }\displaystyle \frac{K(\omega )}{z-\omega }=n(\omega )
\end{array} \right. $$