谷 克彦
科学の発展局面で,それが必要としている数学が用意されていたというのは,ドラマティクです.そのような脚色をした本も多いようです(分献1).しかし,必要な数学が手品のように出現したわけはなく,その数学の源泉にはやはり語るべき背景があります.
科学の発展と平行し,それに必要な数学が開拓されるのは興味深いものです.数学と基礎科学は,密接に牽引しあいながら発展してきました.R.クーラントは,”物理数学の方法”の序文(1924)で,次のように述べています.「...多くの数学者は物理学その他の分野との関連を見失い,一方,物理学者は数学者の関心と問題意識,その方法と語法が理解できなくなっている.これでは,科学の発展の流れは次第に細かく枝分かれし水量を失い,ついには干上がってしまうであろう...」(文献2)
数学月間の趣旨は,数学が種々の分野に影響を与え,「数学が社会を支えている」ことを,専門家でない一般の人に説明することです.数学嫌いの一般の人々が,数学は知的遊戯で自分の生活には関係ないと思っているとすれば,その誤解を解かねばなりません.
数学が基礎科学を支えているのですが,それにもまして,その数学は基礎科学を源泉にして生まれたことを,ここで述べたいと思います.
中谷宇吉郎は随筆”科学と文化”(昭和12年)のなかで,科学の普及に役立つ文章作法に4つのタイプを挙げ,そのうちでも,テーマを不思議と感じた所から,今までに知られた事実を列挙することを特に推奨しています(分献3).この手法に則りこの小論を進めようと思います.
1. 外界を知る手段としての数学
我々は感覚(センサー)により,森羅万象を知ることができます.しかし,森羅万象を動かしている外界は,感覚では知り得ず数学の力により初めて知ることができます.始めに,外界についてのクラインの言葉を引用します.「感覚では知り得ない外界がある.数学の目標は,感覚では知り得ない外界を知ることである.そこから予想もしなかった知識,時には感覚と矛盾するような知識が引き出される.それは物質界の知識の精髄であり,感覚をはるかに凌駕している.」(文献4)
例えば,天体の運行を調べて,それを支配している外界の原理を知るには,数学が必要でした.これは,ニュートンにより完成されます.すなわち,運動方程式と万有引力の式から,2体問題ならすべての運動が説明できます.巨大な宇宙の星雲の運動から,分子の集合である気体の圧力などの巨視的性質まで,宇宙のあらゆる力学現象(粒子間の相互作用は無視)を説明し,ニュートン力学と電磁気学(マックスウェル方程式)の2つのパラダイムにより,森羅万象の外界が解明できたと思われ19世紀が終わりました.
2.ニュートンの解明した外界
ニュートンの時代に遡ってみましょう.ニュートンがプリンキピアを刊行したのは,1687年,44歳のときです.若き日のニュートンは,1676年2月5日のフックへの書簡に,「私が,ほかの人たちよりわずかでも遠くを見たとすれば,それは巨人たちの肩の上に乗っているからです」と書いています(注1).巨人たちとは,ガリレオを始めとする先人の研究や数学の蓄積のことで,これらが彼の研究の基礎になったと言っているのです.
しかし,ニュートンの力学に必要だった微積分が用意されていたわけではありません.自分自身で開拓せねばなりませんでした.ニュートンより少し早いと言われますが,独自にライプニッツも同等な業績を上げます.日本でも関孝和がおります.遅かれ早かれ,まさに微積分の扉が開かれる時代の流れではありました.
ニュートンのプリンキピアは,「観測できる事物の因果関係を示す」という立場を堅持しています.引力がなぜ発生するかは言及せず,従って仮説は何もありません.これが,今日の科学的方法論の手本であります.
ポアンカレは,「科学と仮説」で,「数学的理論は事物の本性を我々に解き示すことを目的とするものではない...そのただ一つの目的は実験が我々に知らせる物理法則に定まった場所を与えることである」(第12章,光学と電磁気)といっています(文献7).
数学と自然科学の違いは,数学は観測事物にこだわらず,どのような仮定から数学的理論を構築してもかまわぬ所にあります.例えば,「引力が距離の逆3乗に比例する」として理論を構築することも価値があります.非ユークリッド幾何学は数学として構築されましたが,今日の宇宙論では実在性をおびております.
-------------------
(注1)
この時代の科学者達は,たいへんまめに文通しています.その上,論文公開のシステムは不完全であったので,揉め事が起こりがちでした.特に,ニュートンは自分が得た結果の大部分を秘密にしており,誰かに督促されるか,他の人が同じことを見出したときになってから,公表に踏み切ったといいます.そして自分の先取権が認められなかったり,批判されたりすると逆上したそうです.(文献5)
フックは,ニュートンより7つ年長で,王立協会の実験主任,後ちに書記でした.協会の書記は,外国の科学会とつながりを保つ要職です.他の協会の書記に手紙を書き,関心のある人々に情報を伝えてもらうのです.
ニュートンは,1672年に,”光と色”の論文を王立協会の雑誌に発表します(文献6).この内容をフックが批判したことから,フックを嫌うようになります.
プリンキピア発表後,力の逆2乗法則は,ニュートンに文通で伝えたものであるとフックが主張し,因縁の論争が再度起こります.フックはバネの伸びと力が比例するというフックの法則で有名ですが,やはり大変多才な人です.1679年のフックからニュートンへの書簡には,惑星の運動を,接線方向と中心方向の運動の合成とする見方が示されています.しかしながら,これらの規則から生じる軌道の証明には,微積分が必要で,ニュートンの業績の偉大さは.そこにありましょう.フックは背中の曲がった背の低い人だったそうで,ニュートンの書簡にある巨人の肩に乗るとは,私は肩に乗れたが,フックには乗れないだろうとの皮肉が含まれているということです.ニュートンは,フックの死後の1703年に,12代目の王立協会会長に就任するや,フックの肖像や実験装置などの業績をすべて消し去ったと言われています.
なお,「巨人の肩に乗った小人は遠くを見ることが出来る」という名言自体は,12世紀のシャルトル(仏)のベルナールの言葉として,ニュートン時代の知識人には知られていたそうです(文献1).
---------------------
3.時間と空間の計測
さらに,ニュートンより前のガリレオ(イタリア,1564-1642年)の時代に遡りましょう.空間と時間の計測は最も基本的なものです.空間の測量は,紀元前に幾何学とともに発達しました.しかし,時間の計測は,地球の日周運動を利用した日時計,あるいは,水時計や砂時計でした.その後,ロウソク時計,線香時計などが生活に現れ,やがて,歯車やゼンマイを用いた機械時計が作られるようになります.しかし,正確な時計は,18世紀の振り子時計まで待たねばなりません.
ガリレオの”振子の等時性”の発見は,エポックメーキングです.正確な時計を持たなかったガリレオ以前の時代には,正確な観測に基づいた運動の研究は不可能だったわけです.振り子を時計に取り入れたのは,ホイヘンス(オランダ,1656年)で,1675年には,ホイヘンスは ヒゲゼンマイのついたテンプ時計も製作し,フランスで特許取得しました(フック(英)も考案した(1664年)と主張します).これが,「世界初の実用的な機械式時計」の始まりです.
ガリレオの発見した”振り子の等時性”は,振り子の周期が,振り子の長さ$$l$$の平方根にのみ比例し,振幅や重りの重さによらないというものです.周期は$$T=2\pi \sqrt{l/g}$$と表せ,現在では$$g$$は重力の加速度で地球の場所により,僅かに異なることがわかっています.正確には,”振り子の等時性”は,振幅が小さいときに成り立つ線形近似です.振幅が大きくなると振り子の周期は長くなります.
$$T=2\pi \sqrt{\displaystyle \frac{l}{g } }\left( 1+\displaystyle \frac{1}{4}sin^{2}\left( \displaystyle \frac{\theta _{0 } }{2} \right) + \cdots \right) $$,ここで$$\theta _{0}$$は振幅の半分の角度.
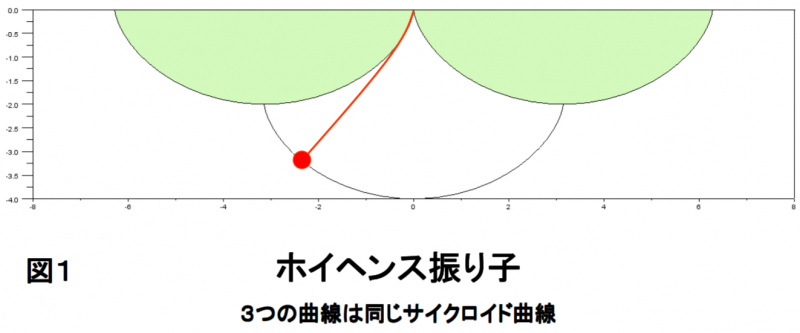
普通の振り子の軌道は,円弧ですが,サイクロイド曲線に沿って動く振り子は,振幅が大きくても小さくても周期は不変です.ホイヘンスは,これを利用したサイクロイド振り子時計も作りました(図1).ホイヘンスは,振り子時計の本と光の本を書き,微積分の先駆的研究もし,ニュートンと重なる時代を生きました.
その後の大航海時代には,海上で正確に経度を知る方法が必要になりました.船の経度は,船の時刻と経度のわかっている地点の時刻の差から求めます.地球は24時間で一回転するから,1時間で経線15度の差です.
1714 年,イギリス議会は「経度を精度良く決定できる方法」に2 万ポンドの懸賞を出しました.時計技師ジョン・ハリソン(イギリス)は,30年近くも試作を繰り返し,苦心の4号機H4はポーツマスからジャマイカへの81日間の航海を済ました(1762年1月19日)に,時計から求めた経度と現地の天文観測から求めた経度との誤差が5秒という議会の要求(2分)をはるかに上回る成績を収めました.
彼は,今日の懐中時計にも使われているグラスホッパー脱進機構を発明しています.(文献8)
--------------------------
(コラム) 現代の標準時計--クォーツ時計,原子時計(文献9)
切り出した水晶(クォーツ)の両側の面に電圧をかけると結晶は変形します.逆に両側から力をかけると両端に電圧(分極)を生じます.この性質を圧電効果といいます.圧電効果は,結晶構造に対称心がある場合には生じません.なぜなら,結晶中のいかなる方向に電圧(分極)ベクトルが生じても,対称心に矛盾するからです.
所定の方位で所定の厚さに切り出した水晶片の両面に交流を印加すれば,水晶片は振動します.水晶片の共振の起こる周波数で安定な発振器を作ることが出来ます.水晶振動子(通常,32.768kHz=$$2^{15}$$Hzの水晶音さ)を用い,精度の高いクオ-ツ時計が作られており,実際の標準時計もこれです.
現在の時間標準は,セシウム($$^{133}Cs$$)の原子時計と定められました.原子時計とは,水晶時計を含む複合システムで,水晶発振器の周波数の校正標準に原子の状態遷移の周波数を用います.
セシウム原子は,最外殻の電子が1つ(水素原子型)なので,解析的にエネルギー準位の計算が出来ます.磁場を印加して縮重している準位を分離させた状態で,基底状態から励起状態への遷移を起こさせると,マイクロ波領域の9.192631770GHzのエネルギーで遷移します.そこで,水晶発振器により,この近傍のマイクロ波を発生させ,セシウム原子による吸収が最大になったときの水晶発振器の周波数を,9.192631770GHzであると校正しています.
ちなみに,GPS衛星は,ルビジュウムの原子時計を積載しています.最近はMEMS(Micro Electro Mechanical Systems)技術により,ルビジュウムの腕時計の開発も進んでいるそうです.
長さの標準は,地球の経線の1/4を$$10,000m$$と定めたのが始まりでした.しかし,1983年に,真空中の光速でこれを定義することになりました.1$$m$$の定義は「光が真空中を1/299,792,458秒間に進む長さ」です.長さの標準にも時間を基礎に置くこととなったのです.
------------------
4. 最小作用(モーペルテュイ)の原理,あるいはオイラーの原理(注2)
モーペルテュイは,「始状態から終状態への運動経路には,作用と呼ばれる積分量が定義でき,作用が最小となる経路が実現される.これが物理学のみならず,万物の運命を決める外界の原理である」という着想-”最小作用の原理”(1744年)を得ました.たしかに,現実の運動では,しばしば作用が極小になりますが,正確には,「作用が停留値をとる経路が実現する」というのが正しいことが後にわかります.
オイラーは,モーペルテュイの作用量の定義を積分に拡張し,最小作用の原理をさまざまな力学課題に適用できるようにし,”最大,または最小の性質をもつ曲線を見出す方法”(1744)を発表しました.これを読んだ若きラグランジュは変分法を発明し,オイラーに手紙(1755)を送ります.オイラーは,ラグランジュの方法を採用し,”変分法の原理”(1766)を出版します.変分法で導かれる運動方程式が,オイラー=ラグランジュ方程式といわれる所以です.その後,ラグランジュは,”解析力学”(1788)を出版します.その序文に「本書には図は一つも出てこない....所定の手続きに従い進める代数計算だけだ....」と高らかに宣言します.こうして,複雑な力学問題も解ける一般化された手法が確立されます(注3).
変分法は,19世紀のハミルトン,ヤコービにより完成に至ります.ハミルトンは,系の状態を表示する空間に,座標と速度を座標軸とした相空間を導入し,「作用量は最小化や最大化するのではなく,停留化する」ことを示しました.
1つの物体は,座標$$x, y, z$$と速度$$\dot{x}, \dot{y}, \dot{z}$$を変数に持ち,その状態は6次元の空間の1点で表現できます.同様に,$$N$$個の物体よりなる系は,$$6N$$次元の空間の1点で表現できます.この空間を相空間といいます.系のエネルギーを$$H(x_{i}, y_{i}, z_{i}, \dot{x}_{i}, \dot{y}_{i}, \dot{z}_{i}, )$$とすると,エネルギーが保存される運動の軌跡は,相空間内の超平面$$H(x_{i}, y_{i}, z_{i}, \dot{x}_{i}, \dot{y}_{i}, \dot{z}_{i})=h$$に含まれます.超平面に描かれる閉曲線に沿った”作用”を停留化する曲線が軌道となるわけです.解けるかどうかは別として,周期解(軌道)が存在することは,証明(1986年)されています.(文献10)
最小作用の原理の理解には,ホイヘンスの光の波動説の説明が参考になります.ホイヘンスは,空間は見えない媒質で満たされており,光は波紋(球面波)が拡がるように伝わると考えました.波面上の各点はまた新たな波源となり,そこを中心として新たな波紋が広がって行きます.生じた無数の波紋は重なりあったり打ち消しあったりの結果,新しい波面ができます.これは多数の波面の包絡面で,この面に垂直な方向に光は進むと考えます.この様なプロセスで決定された方向は,作用を停留値にするものです.
量子力学の世界の運動には,軌道の概念がなく,電子などはランダムに動き回ります.しかし,我々の日常(マクロ世界)では,電子の運動でも軌道はあります.ここで,マクロ世界でも物体はランダムな経路をとれるとしてみましょう.あらゆる経路に実現可能性があるが,各経路の実現率は,それぞれの確率に従う.これらの確率は,波紋が伝播するときのように互いに干渉し合い,その結果として現実の経路が決まってくると言うわけです.最も確からしい経路は,近くからの干渉の最も少ない経路であって,これがちょうど作用積分を停留化するもののようです.「ファインマンの原理」(文献10)
運動方程式が解ける問題を”可積分な問題”といいますが,実際は,”非可積分の問題”がほとんどです.ニュートン力学は,可積分で安定な周期軌道が解になる特殊な範疇を扱っています.一方,非可積分の問題からは,カオスが生じます.1つの軌道は,1本の因果列の存在を意味しています.単純な世界は,今日の現象(原因)1が明日の結果1につながり,今日の現象(原因)2が明日の結果2につながる世界ですが,一般には,今日の現象のすべてが,明日のある結果1の原因になりうる複雑な世界です.バタフライ・エフェクトという映画(注4)があったようですが,今日,上空で蝶が羽ばたいたことが,遠い未来に竜巻きを起こす原因の一つになるかも知れません.「風が吹けば,桶屋が儲かる」世界です.この世界は,独立な因果列はないので,周期的な軌道にはなりません.コンピュータを用いて,すべてのステップを計算していけば,結果を予測できるのですが,遠い先の結果は予測もつかないものになります.「最小作用(停留値)の原理」は,ニュートン力学も含むが,このようなカオスも含む原理であります.
--------------------------------
(注2)
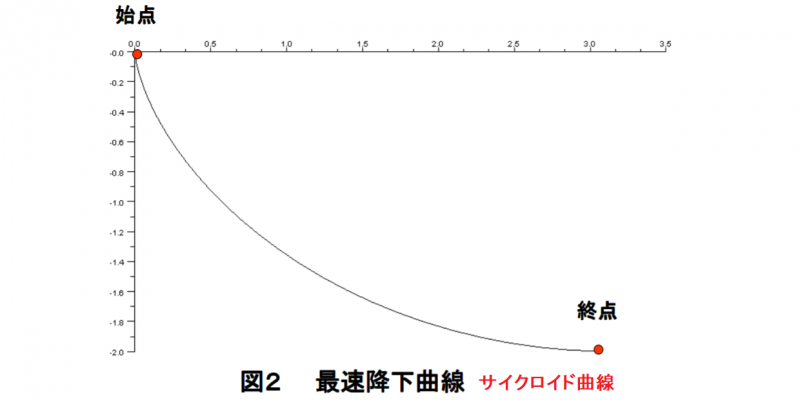
最小作用の原理の起源といえば,1696年のスイスの数学者ヨハン・ベルヌーイの”最速降下曲線”問題に言及せねばなりません.「決まった二点の間を,始点から終点まで玉が一番速く転がることが出来るような曲線を求めよ」という問題です.ライプニッツの提案により,ベルヌーイはこの問題を海外の数学者にも公開することにしました.ベルヌーイは,ライプニッツの友人で,ニュートンとライプニッツの微積分の先取権論争にも加わり,ライプニッツを応援しています.きっと,ニュートンを困らせてやろうと思ったのでしょう.ところがこの問題を受け取ったニュートンは,「当時,造幣局の仕事で忙しく疲れて帰宅したが,問題が解けるまでは寝なかった.とは言っても朝4時までには解けてしまった」と日記に書いています.そして,解答を匿名で返したということです(文献1,5).
最速降下曲線の答えは,円板の縁(1点)に目印をつけ,直線上を転がしたときに,目印が描く”サイクロイド曲線”です.ホイヘンスが振り子時計に用いたあの曲線です.
(注3)解析力学の手順
力学系を記述するラグランジュ関数 を求め,ラグランジュ関数の作用積分が停留値をとる条件を変分法で解くと,オイラー=ラグランジュ方程式が得られます.簡単な系のラグランジュ関数は,(運動エネルギー)-(位置エネルギー)の型になりますが,複雑な系では,位置エネルギーが速度に依存することもあります.
ラグランジュ関数は,電磁場に置かれた荷電粒子にも定義され,光(電磁力学)も力学も統一して扱える原理であります.変分原理から,ニュートンの運動方程式は導出されます.その上,変分原理はニュートン力学よりさらに一般化された外界の原理です.(文献11)
20世紀に入り,量子力学が誕生するときにもこの原理が手がかりになりました.
光や物体の運動が,作用積分を停留化するような,手の混んだ経路を選択するというのは,何と不思議なことでしょう.
(注4)
過去に戻れる能力を持ったエヴァンは,過去に戻りやり直すことにする.しかし,過去に戻り選択肢を変えて始めた人生は,どれも,自分を含め自分が愛する誰かが,幸せではないものだった.
--------------------------------
5. 結晶の世界
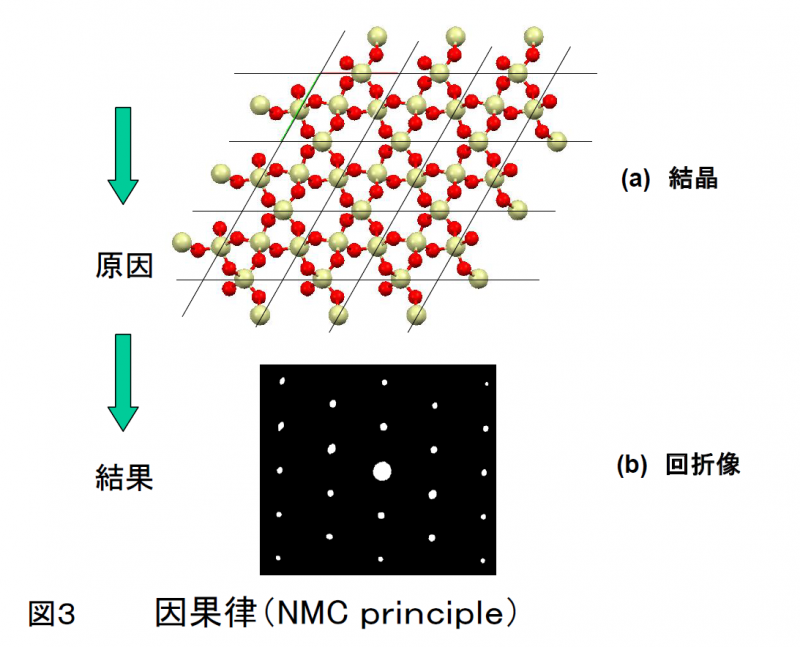
結晶は,原子や分子が規則正しく並んでできています.水晶の結晶構造を図3(a)に示します.簡単のため$$c$$軸に沿って投影した平面図にしました.大きい丸は,シリコン原子,小さい丸は酸素原子です.図3(a)を見ると,基本タイルで,平面が隙間なく張り詰められているのがわかります.実際の結晶は,基本ブロック(平行6面体)を隙間なく積み重ねた3次元に周期を持つ構造です.結晶の基本ブロック(単位胞といいます)は,一辺のサイズが$$nm$$の程度なので,その実在を観測したのは,X線の発見(レントゲン,1895年)以降になります.発見まもないX線は,波長の短い($$nm$$オーダー)光らしいので,空間に周期を持つ結晶が回折格子になるだろうとラウエは考えました.これが有名なラウエの実験(1912年)です.結晶が持つ対称性は,その回折像の対称性に反映されるはずです(”因果律”図3).逆に,X線回折像から結晶構造を推定できるわけで,その手法は,ブラック親子により開発(1915年)されます.この時点で,結晶構造解析に必要な,空間群タイプ230種類の数え上げは,「さあ,お使い」とばかりに準備されていました.何とドラマティックでありましょう.
しかしながら,ここで空間群を突然出現させるのは演出にすぎません.それが生まれるまでの背景を辿って見ましょう.結晶は単位胞が積み重なった「デジタル世界だ」という推論は,18世紀後半に遡ります.(文献12)
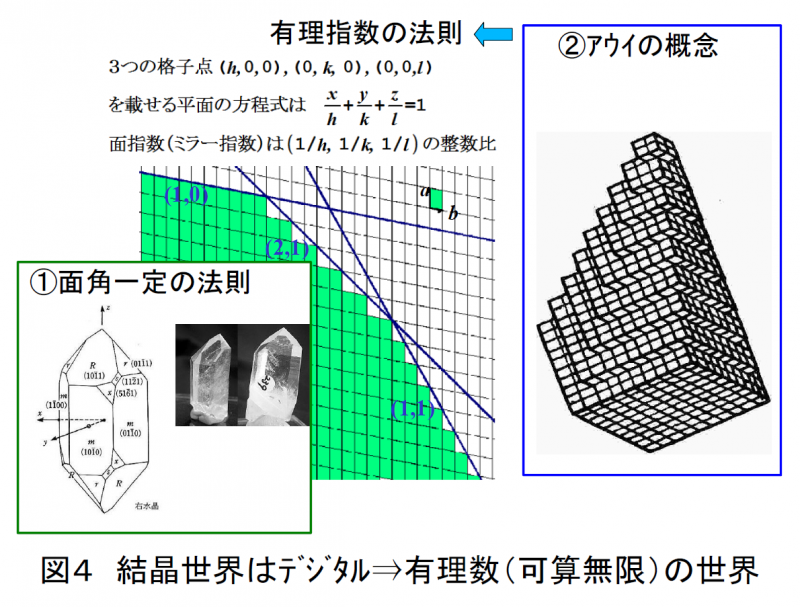
デンマークの鉱物学者ステノ(1669年)が,水晶で発見して以来,種々の鉱物結晶の外形の研究が積み重ねられ,「同一物質の結晶では,対応する面と面のなす角度は一定不変である」という法則(1772年)を,フランスのリスルが確立します.
アウイ(1783年)は”有理指数の法則”を見出します.方解石は劈開が顕著で,どこまでも同じ形の平行6面体に割れます.これなどは,単位胞の存在や,結晶格子の存在を思わせます(図4).結晶が単位胞の積み重ねでできるデジタルの世界ならば,観測されるどの結晶面も,格子点を載せた平面だから,結晶面の座標軸上の切片の比は,必ず整数比になるはずです.これが有理指数の法則の心です.結晶面の記載に用いるミラー指数は(1839年)に考案されました.これらの観測事実から,結晶は単位胞が並んだデジタル世界でなければならないと推論されました.
基本タイルを点で表すと,結晶構造は点の配列になり,このような点の配列を格子といいます.つまり結晶はデジタル(離散量)の世界です.格子の対称性タイプの数え上げ14種(ブラベー,1848年)がなされます.また,結晶外形の対称性から,結晶点群の数え上げ32種(ヘッセル,1830年)がなされました.
結晶点群と格子(並進群)の組み合わせで,結晶空間群が生成されます.1890~1894年に,フェドロフ,シェンリース,バーローがそれぞれ独立に,3次元の空間群230種類を数え上げました.(文献13)(注5)
---------------------
(注5)
結晶空間群には,並進群が正規部分群として含まれています.
基本タイルを点にしてしまうような写像なら,空間群に含まれる格子があぶりだされます.格子の周期で並進した物は同値とみなすならば,空間に広がった結晶構造や平面にひろがった繰り返し模様は,1つの単位胞の中に集約され,空間群は結晶点群に準同型となります.(文献13,14)
---------------------
6.おわりに
「科学者がその肩に乗ろうと懸命に探し求めた巨人は,とうの昔に死んだ数学者だった.しかし,数学者の側からみれば,自分が科学者の肩の上に乗っていた,などということはまずありそうにない」(文献1)という見方もあります.しかし,私は,新しい数学の誕生は,その背景に,科学の発展があったことに注目し,大きな過去の世界からこの小論への写像を試みました.論点を浮き彫りにするには,準同型写像です.同値と見做そうとする項目は束ねて,写像の核にすると,大きな世界にあった特徴の一つが浮き上がります.写像の核は,数学自体にしたので,数学と他の基礎科学の関係が見えたでしょうか.この先,”線形写像の世界”を訪れる予定でしたが,紙数が尽きました.これに関しては,拙著(文献14)をお読みいただけると幸甚です.
―――――――――――
参考文献
1.物理と数学の不思議な関係,マルコム・E・ラインズ(青木薫訳),ハヤカワ文庫, 2004
2.数理物理学の方法,クーラン,ヒルベルト(斎藤利弥監訳),東京図書,1985
3. 中谷宇吉郎随筆集,樋口敬二編,岩波文庫,1988
4.何のための数学か,クライン(雨宮一郎訳),紀伊国屋書店, 1987
5.古典物理学を創った人々,エミリオ・セグレ(久保亮五,矢崎裕二訳),みすず書房,1992
6.http://trailblazing.royalsociety.org/
英国王立協会は,2010年11月30日で創立350周年になります.これを記念し,17世紀から協会が発行しているPhilosophical Transactions誌に掲載された論文の科学史的に重要ないくつかが,このwebsiteで公開されています.
7. 科学と仮説, ポアンカレ(河野伊三郎訳),岩波文庫, 1966
8. http://www.nmm.ac.uk/harrison
9.尾上守夫,私信 \\
10.数学は最善世界の夢を見るか?,エクランド(南條郁子訳),みすず書房, 2009
11.理論物理学,カンパニエーツ(山内恭彦,高見穎郎訳),岩波書店, 1964
12.結晶の話,伊藤正時,斎藤喜彦,倍風館,1984
13.結晶の幾何学,谷克彦,数学教育p.41-46,明治図書,2003.11
14.物理と工学で使う行列と固有値,谷克彦,技術評論社, 2010
-----------------------------------
「数学文化」,NO.15(2010),p.79-87 より