by the Plus Editors Rachel Thomas and Marianne Freiberger.
この数週間によく聞く2つの言葉に,集団免疫と基本再生産数$$R_0$$と呼ばれる数(R noughtと言う)があります。
基本再生産数
COVID-19などの感染症を考えると,$$R_0$$は病気の基本再生産数です.つまり,集団のすべての人が病気への感染感受性がある場合,感染者が感染させる平均人数です.COVID-19の場合,この数は現在2から2.5の間にあると推定されています.季節性インフルエンザの場合,0.9から2.1の間です.そして,はしかの場合,それはなんと12から18です.
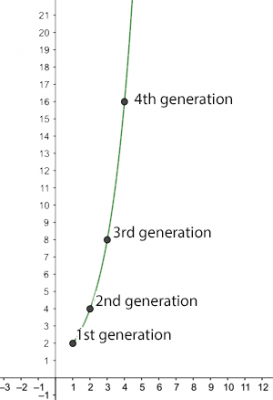
$$ R_0 $$が十分に大きいと,病気が急速に広がるのがわかります.たとえば,$$ R_0 $$が2の場合,1人の感染者が次のような新しい感染の増加を引き起こします.
第1世代:新しい感染$$ 2 $$
第2世代:新しい感染$$ 4 $$
第3世代:新しい感染$$ 8 $$
第4世代:新しい感染$$ 16 $$
$$ n $$世代の新しい感染は$$ 2 ^ n $$です.患者の感染性が続くのが1週間だとすると,この率では,全世界の人口(78億人)は32週間強で感染します.
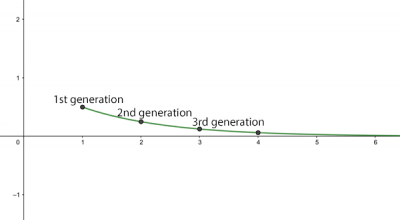
基本再生産数$$ R_0 $$が1未満の場合,非常に異なる描像になります.例として,$$ R_0 = 0.5$$とします.明らかに,感染した人は半分の人に感染させるとはできませんが,これは平均であることを覚えておいてください.つまり,10人の人が 他の5人に感染させる,または100人が他の50人に感染させると想定します.前と同じように,最初に感染者が1人いると仮定すると,新しい感染の数は次のようになります.
第1世代:新しい感染$$ 0.5 $$
第2世代:新しい感染$$ 0.25 $$
第3世代:新しい感染$$ 0.125 $$
第4世代:新しい感染$$ 0.0625 $$
$$ n $$世代の感染は$$(0.5)^ n $$件の新しい感染があります.世代の数$$ n $$が大きくなるにつれて,この数はますます小さくなり,病気は消滅します.
$$ R_0 = 1 $$の場合はどうでしょう? この場合,病気は風土病endemicになります.常に集団に存在しますが流行epidemicはありません.
実効再生産数
それでは,はしか,あるいは季節性インフルエンザの株いくつかは$$ R_0 $$が1より大きいのに,なぜ全世界がずっと前にこれらの疾患に感染していないのでしょうか?その理由は,集団のすべての人に感受性があるとした場合の感染した人が感染させる平均人数が$$ R_0 $$でしたが,その世界にいた人は免疫力がなく,予防ワクチンがない条件です.実際には,他の場所で病気に感染した人が,これまでにその病気がなかった世界に入ったからです.
$$ R_0 $$が$$ 2 $$の場合,前述のように,最初は感染者の数が急激に増加します.
しかし,いったん人が病気から回復したら,彼らは(うまくいけば)ある程度の免疫を獲得するでしょう.つまり,しばらくすると,完全な感受性のある集団ではなくなります.集団の一部の人々が影響を受けない理由は他にもあります.彼らは他の理由で免疫があるかもしれないし,あるいは,ワクチンがある場合彼らはそれを接種したかもしれないし,他の集団から隔離されているかもしれません.
実際の状況では,病気の実効再生産数を調べる必要があり,$$ R $$で表します.一部の人が免疫を持っている(または他の介入が行われている)集団で感染者が感染させる平均数です. もちろん $$ R_0 $$と$$ R $$は関連しています.病気に感受性のある集団の割合を$$ s $$と書くと,
$$R=sR_0$$
例として,集団の半分だけが感受性がある場合,$$ s = 0.5 $$,$$ R = 0.5R_0 $$になります. この場合,$$ R_0 $$が$$ 2 $$以下の場合,$$ R $$は$$ 1 $$以下であり,病気は伝染病になりません. ワクチン接種であれ,社会的距離であれ,あらゆる介入の理想的な目的は実効再生産数を1未満にすることです.
集団免疫
これは,集団免疫とどう関係があるのでしょうか?集団免疫の背後にある一般的な考え方は,多くの人々が免疫を持っている集団では,病気の感染が広がらない.それによって免疫のない人々を守るので,この集団は脆弱な個人を保護します.
それでは,集団免疫を獲得するには,集団の何人が免疫を必要とするのでしょうか? 病気の基本的再生産数が$$ R_0 $$で,1より大きいため,伝染病の脅威になると想像してください.私たちが見てきたように,実効再生産数$$ R $$が1未満の場合は,この病気はやがて消滅します. したがって,集団免疫を達成するには,実効再生産数$$ R $$を1未満にする必要があり,$$ R = sR_0 $$,$$ s $$は感受性のある人口の割合なので,
これを並べ替えると、
$$s <1 / R_0$$
つまり,集合中の感受性のある人々の割合を$$ 1 / R_0$$未満にする必要があります.これを実現するには,何人の人々が免疫力を必要とするのでしょうか.感受性の高い人の割合が$$ s $$である場合,感受性のない,つまり免疫のない人の割合は$$ 1-s $$です.
$$s <1 / R_0 $$ ということは, $$1-s> 1-1 / R_0$$
集団免疫を達成するには,少なくとも人口の$$ 1-1 / R_0 $$の割合が免疫を持つ必要があります. $$ R_0 $$が2.5(COVID-19の推定値の上限)の場合,これは少なくとも免疫力のある集団の$$ 1-1 / 2.5 = 0.6 $$,60%に相当します.
どうやって達成するか?理想的には,人口の少なくとも60%にワクチン接種することです.ワクチンがなければ,このレベルの免疫が病気になり免疫されることによって自然に達成されることを期待します.しかし,多くの人がCOVID-19で亡くなっているので,感染を増やすと免疫力が高まるという知識に自信をもって,集団全体に適用できません.
世界中の多くが現在封鎖されているのは,脆弱な人々と私たちの医療システムを保護する必要があるからです.皮肉なことに,封鎖とは,私たちの多くが感染したことによる免疫力を獲得していないことを意味します.
それでは,この最悪のシナリオで何をすべきでしょうか? 1つのオプションは,ワクチンができるまでロックダウン状態を維持することですが,それは1年以上かかる可能性があります.もう1つは,間欠的なロックダウンを行って,流行の急増をヘルスケアシステムの重要な能力より低く保つことです.
現時点では,誰も将来何が起こるか正確には知らないのです.私たちの知識にもとづく推論は,パンデミックの経過を予測しようとする数学的モデルに基づいています.私たちの現在の苦境から最善の出口戦略を見つけるために,緊急の呼びかけが科学モデリングコミュニティに出ています.
上記の計算は,ワクチン接種に関する重要なメッセージも送信します.これは,病気の予防接種を受けている個人を保護するだけでなく,何らかの理由で予防接種を受けず,したがって脆弱な人々も保護します.予防接種はあなたのためだけではなく,集団全体のためです!