https://elementy.ru/posters/fractals/H-fractal
Hフラクタル
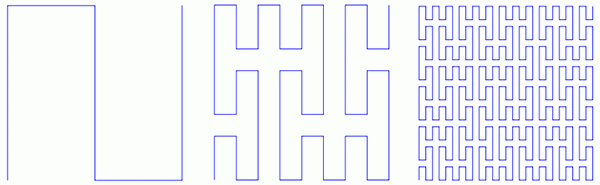
文字Hの形の図形からすべてが始まります。Hの垂直な線分と水平な線分の長さは等しくなっています。
次ステップで、図の4つの端のそれぞれに、半分に縮小されたコピーが描画されます。
次ステップで,両端にあるのは,4分の1に縮小された16個のHです。
このように無限に繰り返して、フラクタルは視覚的にほぼ正方形を埋めます。
Hフラクタルはどの場所でも密。つまり、正方形の任意場所のいくらでも小さい近傍に、フラクタルがあります。よく見ると、各文字Hが、同じステップで完成した独自の小さな正方形に含まれていることがわかります。

Hフラクタルは正方形を埋める(空間充填曲線)ので、そのフラクタル次元は2で、すべてのセグメントの全長は無限大です。
Hフラクタルを構築する原理は、電子マイクロ回路の製造に使用されます。複雑な回路内の多数の要素が同時に同じ信号を受信する必要がある場合、Hフラクタルの適切な反復セグメント端に配置し、接続します。
オプション
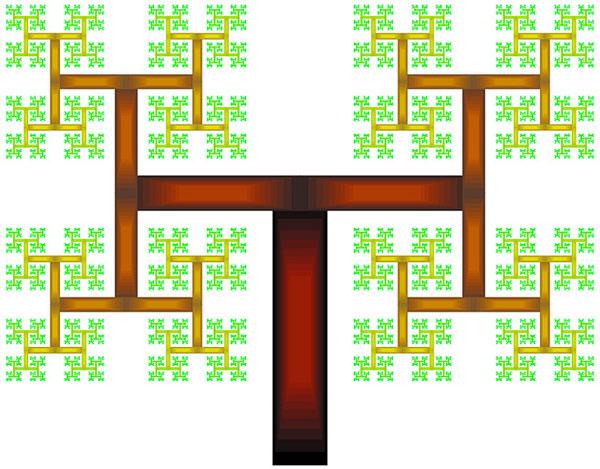
Mandelbrotマンデルブロの木は、線セグメントではなく長方形でできた厚いHを描画することで作られます。
www.flickr.com/photos/29915793@N08からの画像
平面の一部を埋める線のいくつかの例(空間充填曲線)は、1890年にイタリアの数学者ジュゼッペペアノの論文に初めて登場しました。Peanoペアノは、曲線と正方形が等しい性質(点集合と見なす場合)である、つまり「同じ」密度の点を持っているということの視覚的な説明を見つけようとしました。この定理は、Georg Cantorカントールによって、彼が創始した集合理論の枠組みの中で証明されていましたが、この直感に反する新理論の結果は、大きな懐疑論を引き起こしました。ペアノの例(セグメントから正方形への連続写像)は、カントールの正しさの良い確認となりました。
ペアノ曲線、最初の3回の繰り返し
不思議なことに、ペアノの論文には1つのイラストも含まれていませんでした。ペアノ曲線という表現は、特定の例ではなく、平面または空間の一部を埋める曲線を指す場合があります。
下の曲線(ヒルベルト曲線)は、1891年にデビッドヒルベルトによって発表されました。見ることのできるのは,私たちの念頭にある数学的オブジェの有限回近似です。本当の曲線は、無限回の操作後にのみ実現します。
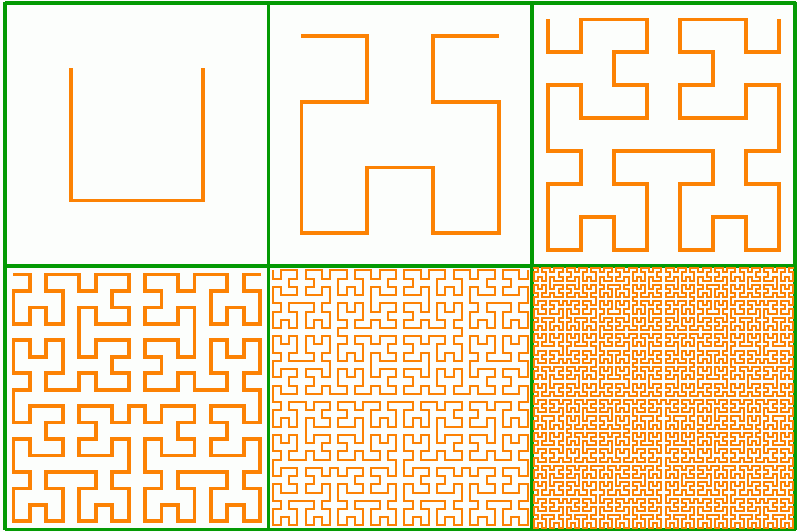
ペアノ曲線の変種-ヒルベルト曲線、最初の6回の反復
ゴスパーカーブ、またはゴスパー雪片(ビル ゴスパー):
ゴスパーの曲線(雪片)
そして、そのような線の三次元版もあります。たとえば、3次元のヒルベルト曲線、またはヒルベルトキューブ:
カリフォルニア大学バークレー校のコンピューターサイエンスの教授であるCarloH.Séquinによって作成された、3Dヒルベルト曲線のエレガントなメタリックバージョン(3回目の反復)。 www.cs.berkeley.eduからの画像
このようなモデルは、64個のプラスチック製コーナー配管を用い自分で作れます。
ヒルベルトのプラスチックキューブ(2回目の繰り返し)。momath.orgからの画像