STXM(走査型透過X線顕微鏡)は,有機材料の化学状態のマッピングができる重要な評価技術です.実験を計画されている方々のお役に立つように,私たちの過去の実験(2000年10月)を紹介しましょう.
■私たちは,1粒のトナーの中に練り込まれている有機物分子の分布状態を知る必要がありました.高精細のトナー1粒のサイズは5~10μmです.その1粒のトナー中には,種々の有機材料(レジン,ワックス,色素,電荷制御剤,など)の分子を練り込んでいます.それらの分子がどのように分布しているか観察したいものです.特徴的な元素を含む分子の分布をみることはさして困難な課題ではありません.蛍光X線を用いれば元素分布のマップを簡単に得ることができます.電子顕微鏡でもエネルギーロスEELSで見ることができます.しかし,トナーの場合は,分布しているのがすべて有機物(炭素原子Cが主体の分子)ですから,蛍光X線分析は役に立ちません.
分子内の炭素Cの結合状態の違いで有機材料を見分ける必要があります.分子のC原子の結合状態(1重結合か,2重結合が,π電子系か,どんな官能基が付いているか)で,炭素の1s電子の吸収端近傍のスペクトルの形がわずかにことなることが手掛かりです.炭素1s電子の吸収端は285eV程度ですので,この付近の吸収スペクトルは,軟X線領域(真空中で測定)になり,この実験のできる装置は,2000年当時は,Hitchcock(McMaster大)教授が,米国バークレイの放射光施設ALSに作ったBL5.3.2とBL7.0でした.エネルギー分解能0.1eV,ビームの空間分解能35nmという素晴らしい性能です(aXis2000という解析ソフトも完成していました).これを用いて2000年から数年間共同実験をしました.
(写真)左からDr. Araki,Dr. Kilcoyne,Dr. Hitchcock
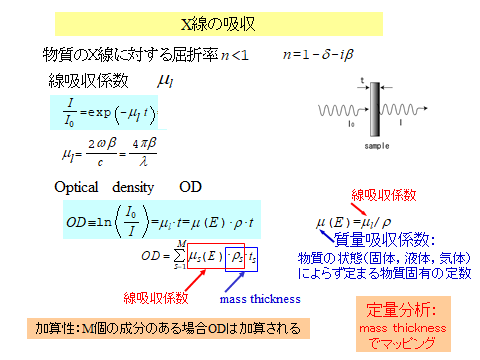
吸収端のちょっと上の50eV~1000eV程度までの範囲に現れるスペクトをEXAFSといい,吸収原子周囲の配位構造の解析に使えることはご存じかもしれません.一方,吸収端近傍のせいぜい50eVまでは,XANESとかNEXAFSと呼ばれます.原子は吸収端のエネルギーを吸収して,光電子波を発しますが,吸収端近傍では電子波の持つエネルギーが小さく波長が長いため多重反射が起こり,周囲の配位原子に反射され吸収原子の位置に作る電場は非常に複雑なので,EXAFSのように配位構造の解析には使えません.しかし,吸収原子周囲の化学状態に特徴的な吸収スペクトルになり,分子を知る手がかり(指紋のような)になります.
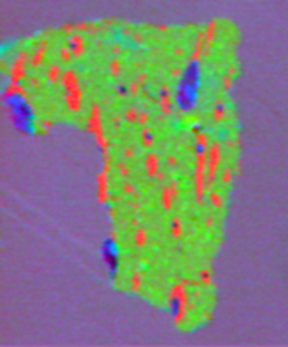
■ここで初期の結果(2000年10月)を紹介しましょう.
2次元にスライスした試料の1点1点ごとに,Cの吸収端付近でX線の波長をスキャンすると,その点に存在する物質分子(一般的に,数種の分子が重畳されている)に特徴的な吸収端に対応して透過X線のコントラストが変化しますから,画面を見ていると物質の分布状態がわかります.上の写真では,エネルギーをスキャンしていくと,赤や青でマークした部分のコントラストが逆転したりして,違う物質が分布していることがわかります.
■用いる数学について
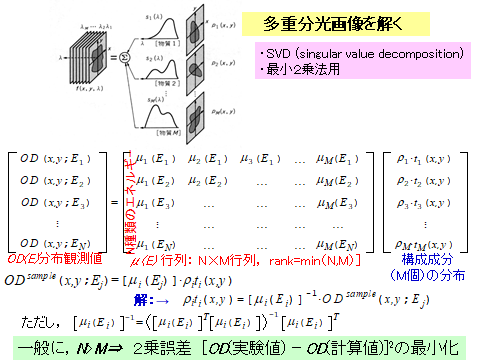
このデータ処理のための数学は特異値分解といいaXis2000で実行します.
X線のエネルギーEのときの,サンプルの点(x,y)のコントラストは,
Σμ_i(E)・t_i(E) ,iは分子の種類,μ_iとt_iは分子iの吸収率と存在量です.
各点(x,y)でΣμ_i・t_iのデータを測定しますが,1画面の測定ができると,エネルギーをΔEスキャンしまた画面の各点を測定するので,Eのステップ数分の各点(x,y)の吸収データが得られます.結局,各点(x,y)でスペクトルが得られたことになります.各点でi種類の分子をどのような比率で混ぜると観測したスペクトルと同じにできるかという問題を解くことになり特異値分解を用います.
研究のまとめは,トナー1粒内の立体的な分布の再現です.各スライス断面で測定し解析した分布を積み重ねて3D像を再現しました.
J.Phys.Ⅳ France 104(2003)509, A.P.Hitchcock, et al.
■ この装置のゾーンプレートの光学系の仕組みはとても面白いのですが,今回はここまでにします.