━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 [2020.08.25] No.335
<<数学と社会の架け橋=数学月間>>
━━━━━━━━━━━━━━━━━━━━
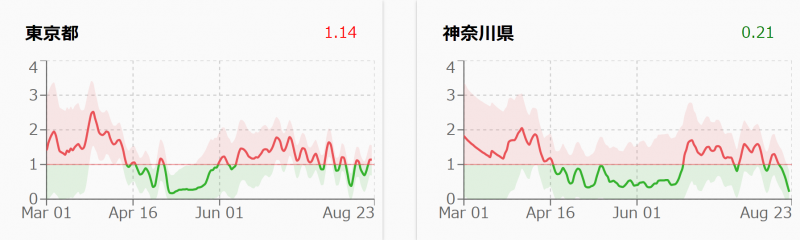
実効再生産数が東京では,まだ1を少し超えているようですが,他の県では1未満になってきたようです.
以下のサイトに,都道府県別の実効再生産数の時系列の変化のグラフがあります.
Rt Covid-19 Japan都道府県別コロナウイルスの感染拡大・収束状況(実効再生産数Rt)をグラフ化したWebサイト
rt-live-japan.com
実効再生産数Rというのは,1人の感染者が新たな感染者を作る人数のことです.
Rが1未満なら感染流行は減少収束し,1より大きければ感染は拡大します.
しかしながら,各都道府県の実効再生産数がすべて1未満になっても,
感染拡大の起こる可能性を警告している論文を前号で紹介しました.その論文では,
全体をコミュニティと病院という2つのグループに分割したモデルで,
コミュニティ内の感染に関する実効再生産数と病院内の感染に関する実効再生産数がともに1未満であっても,
全体の実効再生産数が1を超す(感染拡大が起こる)可能性が指摘されました.
その原因は,コミュニティから病院に感染させる場合も,病院からコミュニティに感染させる場合もあるからです.
都道府県別の実効再生産数が,それぞれ1未満になっても,各県間の人の移動接触により各県間の感染が起こるので,
全体の実効再生産数が1より大きくなることは十分あり得ます.油断は危険です.
■数学の形式としては,次の行列を作ります:
対角要素には,各都道府県の実効再生産数を並べ.行列のその他の要素には,異なる県間の感染率を対応させます.
県間の感染率は,相当する県間の人の接触確率のようなものです.
このような行列を作るにはいろいろなデータが必要ですが,この行列ができたとすると,
この行列の固有値を求める数学の問題になります.最大の固有値が1を超していれば,
全体の実効再生産数は1を超し伝染の拡大が起こります.
私たちの社会は,都道府県がそれぞれ孤立して独立でいるわけではなく,
互いに相互作用(人の接触がある)しているので,
独立な個別地区の予測と,全体の予測は大変異なり,このような計算をしてみないとわかりません.
(注)実効再生産数の計算方法は,Anne RがCoriらによるものが,山中伸弥のホームページに紹介されています.