■楕円幾何平面の正則タイル張り
球表面が球面正p多角形タイルで{p,q}のように張りつめられているとき,1つのタイルの中を2p個の直角3角形に分割できます.この直角3角形を鏡室とする万華鏡を“メビウスの万華鏡”と名付けます.このときの直角3角形(鏡室)の内角は,それぞれ π/p,π/q,π/2で,この直角3角形を(p,q,2)と略記します.
■双曲幾何平面の正則タイル張り
ポアンカレ円盤の双曲幾何平面が,双曲正p多角形で{p,q}のように張りつめられているとき,1つのタイルを2p個の直角3角形に分割できます.この直角3角形を鏡室とする万華鏡を“コクセターの万華鏡”と名付けます.
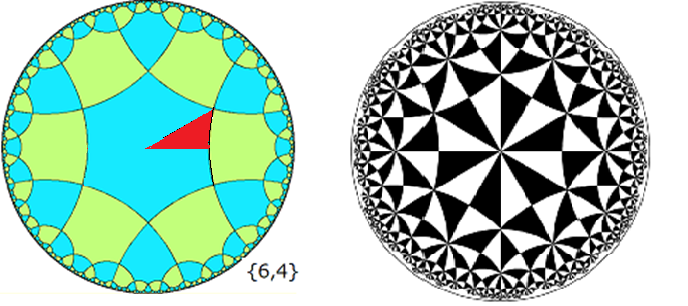
双曲面の{6,4}正則分割を例に,直角3角形(6,4,2)(赤い3角形)を図(左)に,対応する“コクセターの万華鏡”の映像を図(右)に示します.
■双曲面{6,4}分割の場合の“コクセターの万華鏡”を作る
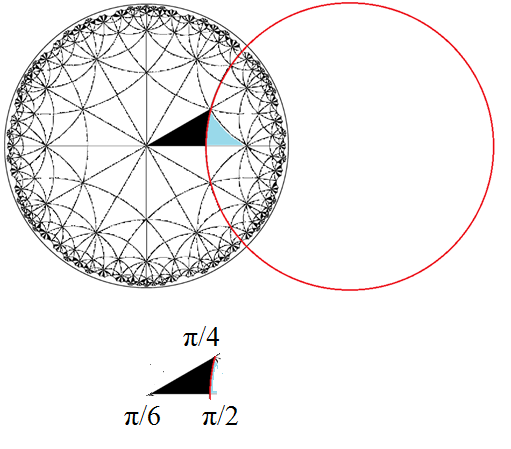
双極面{6,4}分割の映像を,3角形の万華鏡で作るには,双曲面直角3角形(6,4,2)を用います.この3角形の2辺は平面鏡,残りの1辺は円盤のフチに直交する円弧鏡よりなります.この円弧鏡は,数学的には反転円として定義できるのですが,現実の円柱鏡の反射には収差があるので,数学の定義のように鮮明な万華鏡映像を作るのは困難です.
■エッシャー作品の生まれるまで
(1) (2) (3)
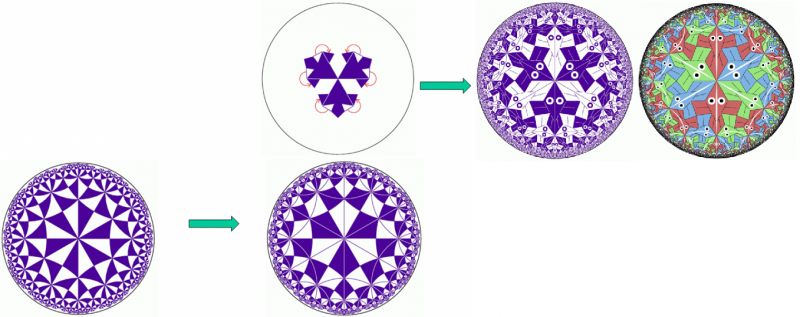
(1)コクセター:直角3角形(6,4,2)による双曲面の{6,3}分割の細分
(2)エッシャー:直線魚のモチーフ
(3)エッシャー:「極限としての円Ⅰ」CircleLimitⅠ
コクセターとエッシャーはオランダで開催された1954年の国際数学者会議で出会いました.1958年にコクセターはこの分割を掲載した論文*をエッシャーに送り,これがエッシャーの「極限としての円」の作品群(Ⅰ~Ⅲ)を生むことになります.
*By S.H.M.Coxeter
Crystal Symmetry and ItsGeneralizations (published in the Transactions of the RoyalSociety of Canada in 1957).