By Julia Gog, Rachel Thomas, Marianne Freiberger
私たちは,伝染病の実効再生産数Rについて考えることに慣れてきました.これは,1人の感染者によって感染する人の平均数です.以前の記事で見たように,Rは伝染の様子かを理解するのに役立ちます.R> 1は流行が拡大することを意味し,R = 1は横ばいであることを意味し,R <1は流行が減少することを意味します.
(私たちがニュースで耳にする実効再生産数Rは,流行の過程で毎日変化します.基本再生数R0とは違います.)
ただし,Rが教えてくれないことの1つは,物事がどれほど速く変化しているかです.これは,Rがレートではないし,関連する時間スケールがないためです.たとえば,ある疾患でR = 2の場合,流行が拡大することはわかります(R> 1であるため). HIVやTBのような病気では,ある人が次の人に感染させるまでに数か月または数年かかる可能性があります.R= 2としても,時間の経過とともにの成長が遅いことを意味します.ただし,インフルエンザ,または,はしかの場合,感染がはるかに速く,日数のスケールでは,R = 2は非常に急速な成長を意味します.
感染流行の成長率はどれくらいですか?
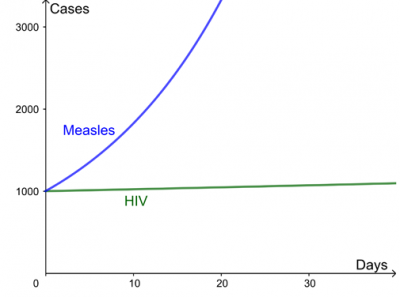
疾患の成長率は,感染症の数が日々急速に変化する速さを捉える自然な方法です.疾患の症例の増加は,指数曲線を使用してモデル化されます.
$$N(t)= {\rm constant} \times e^{\lambda t}$$
ここで,$$N$$はケース数であり,日数で測定した時間$$ t $$に依存します.$$ \lambda $$は,1日あたりの疾患の成長率と呼ばれるものです. ($$ e $$という数値は,約2.719に等しい数学定数であり,指数関数的成長と密接に関連しています.)
上記の曲線の例では,HIVの成長率は1日あたり$$ \lambda $$ = 0.002で,はしかの場合は1日あたり$$ \lambda $$ = 0.06です.この例の両方の疾患が同じ再生産数を持っているにもかかわらず,これは翌月に大きく異なる結果をもたらします.
以下の対話機能を使用して、さまざまな成長率で疾患の進行がどのように変化するかを調べることができます(スライダーを使用して$$ \lambda $$の値を変更します)。--略
COVID-19のパンデミックの間,新しい症例数と新しい死者数が毎日報告されています.これらは3月と4月上旬に英国で増加し,ここ数週間で減少しているのを見ました.増加率が正の場合,毎日新しい感染数は増加します.増加率が0の場合,新しい感染数は一定のままです. 流行を抑制し続けるために必要なことは,成長率がマイナスになることであり,それゆえ新しい感染数が減少することです. 新しい感染数が昨日から3%減少した場合,その増加率は、およそ,1日あたり$$ \lambda $$ = -0.03です. (これは完全に等価ではありませんが,$$ \lambda $$の一般的な値の適切な近似値です.成長率は実際には複利のように機能します.ここで確認できます.)
Rと成長率のどちらが優れていますか?
実効再生産数$$ R $$と成長率$$ \lambda $$はどちらも,疾患の成長を理解するための有効な尺度です. それぞれに適した用途を概説します.
--------
◆再生産数:R
Rは、流行を止めるために必要な介入の強さを理解するのに自然であり、制御手段を計画するためにより適切です。例えば:
R = 1.5は、感染率を3分の1に減らす必要があることを意味します。
R = 2は、影響を受けやすい人々の半分にワクチン接種する必要があることを意味します(この計算については、注*)。
したがって、Rは、流行を止めるために必要な将来の介入の強さを予測する直感的な方法を提供します。
R> 1指数関数的成長
R = 1フラット
R <1指数関数的減衰
R感染発生の数で,レートではありません。時間スケールは含まれていません。
Rは実際には簡単に測定できませんが、感染の時間スケールがわかっている場合は、モデルを使用して適合させることができます。原理的には、だれが誰から感染したかに関する正確な疫学的データによって推定することができますが、これは通常の設定では通常は実行できません。
◆1日あたりの成長率:$$ \lambda $$
成長率は、ケースが時間とともにどのように変化するかを考えるのに自然です。例えば
$$ \lambda $$ = 0.01 /日は、ケースが1日あたり約1%増加することを意味します。
$$ \lambda $$ = -0.02 /日は、ケースが1日あたり約2%減少することを意味します。
成長率は、現在何が起こっているかをよく説明しています。今日特定の数がある場合は、明日、翌日などに何人になるか予測できます。
$$ \lambda $$> 0指数関数的増加
$$ \lambda $$ = 0フラット
$$ \lambda $$ <0指数関数的減衰
成長率$$ \lambda $$は、通常COVID-19の日数で与えられる率です。
成長率$$ \lambda $$は、ケースまたは死亡の時系列データから比較的簡単に推定できます(ただし、少数については以下を参照してください)。単純なアプローチは、ログに記録されたケースの勾配を見つけることです。時間とともに変化する成長率、または不均一な人口を考慮に入れることができるより高度なアプローチには、再び流行モデルのフィッティングが含まれます。
--------
病気の発生率が非常に低い場合や、調査しているコミュニティの人口が非常に少ない場合など、症例数が少ない場合、再生産数と成長率の両方を推定することは特に困難です。その場合、日々の変動が病気の根本的なパターンを簡単に覆い尽くす可能性があるため、成長率についての不確実性が大きくなります(したがって、信頼区間が広くなることが期待されます)。
どのようにしてRから成長率に、またはその逆に到達しますか?
Rと成長率の正確な関係は単純ではありません。次の感染までの各タイミングを考慮する必要があります。大雑把な近似は
$$ R = e ^ {\lambda T} $$
ここで、$$ T $$は平均生成時間です。感染から次の感染までの時間です。
さらに高度な数学も知りたい
これはすべて、制御手段と病気にかかりやすい人の数があまり速く変化していないことを前提としています。
1人の感染者に続いて、感染後の時間を$$ \tau $$(日数)で示します。彼らは平均して他の$$ R $$に感染し続けます。これらのそれぞれについて、感染のタイミングは確率密度関数$$ f(\tau)$$で分散されます。次に、(数学の学部生のための演習!)$$ R $$と$$ \lambda $$は次のように関連付けられます。
$$R ^ {-1} = \int _ {\tau = 0} ^ {\infty} e ^ {-\lambda \tau} f({\tau})d \tau $$
これはラプラス変換または生成時間分布のモーメント生成関数と非常に密接に関連しています。
生成時間の特定の分布(ガンマ分布など)の場合、これは簡略化できることがあります。生成時間を$$ T $$のように正確に一定にすると、$$ R = e ^ {\lambda T} $$が回復しますが、これは実際の多くの感染症のかなり大まかな近似です。
$$ f(\tau)$$は、潜伏期間などの生物学的事柄や、症状があるときに他の人とまだ混合しているか、自己隔離しているかなどの社会的要因に依存します。
詳細については、WallingaとLipsitchによるこのペーパーを参照してください。
----------
この記事について
レイチェルトーマスとマリアンヌフライバーガーはPlusの編集者であり、ケンブリッジ大学の数理生物学の教授であるJulia Gogと共同でこの記事を作成しました。 Gogは、その結果を緊急事態用科学諮問グループ(SAGE)にフィードするモデリンググループSPI-Mのメンバーです。彼女はまた、王立協会が率いる全国コンソーシアムの運営委員会のメンバーであり、COVID-19パンデミックに対処しています。