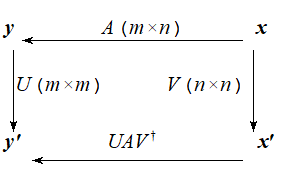特異値分解について★

■特異値分解とは

$${m}$$行$${n}$$列($${m\geq n}$$) の任意の実行列$${A(m\times n)}$$は，$${A=U^{T}\mit\Sigma V}$$，$${UAV^{T}=\mit\Sigma}$$のように分解できる．

ここで $${U ，V}$$ は，それぞれ $${m}$$次，$${n}$$次 の直交行列．$${\mit\Sigma(m\times n)}$$ は，対角成分が正 （$${\sigma_1\geq\sigma_2\geq\cdots\geq\sigma_r >0}$$，$${r}$$は$${A}$$のランク）で，それ以外の成分はすべて 0の行列である．このような分解を特異値分解 (singular value decomposition) と言い，任意の行列に対して可能であることから，工学や物理学でしぱしば活用される．特に，行列$${A}$$が$${m=n}$$である場合が固有値分解であり，分解された$${\mit\Sigma}$$の対角成分を固有値と呼んだ．固有値問題の拡張が特異値問題で，固有値に対応する概念が特異値である．

もちろん，これらの分解は$${A}$$が複素行列である場合にも成り立つ．実行列の場合は，$${U,V}$$は直交行列だが，複素行列の場合はユニタリー行列で，例えば，$${U}$$の逆行列は，転置行列$${U^{T } }$$でなく，共役転置行列$${U^{\dagger} }$$になる．この場合も特異値はすべて正である．一般に，エルミート行列（対称行列）の固有値は実数で，異なる固有値に属する固有ベクトルは互いに直交する．
$$\mit\Sigma (m×n)=\left[ \begin{array}{@{\,} cccc @{\, } }
\sigma _{1} & & & 0 \\[0mm]
& \ddots & & \\[0mm]
& & \sigma _{r} & \\[0mm]
& & & \\[0mm]
& & & \\[0mm]
& & & \\[0mm]
0 & & & 0
\end{array} \right] =\left[ \begin{array}{@{\,} cc @{\, } }
\mit\Sigma _{r} & 0_{n-r} \\[0mm]
0_{m-r,r} & 0_{m-r,n-r}
\end{array} \right] , \sigma _{1} \ge \sigma _{2} \ge \cdots \ge \sigma _{r} > 0$$

■線形写像 $$ y=Ax  (x∈C^{n}，y∈C^{m})$$があり，それぞれの空間でユニタリー変換； 
$$ x'=Vx$$, $$y'=Uy$$をすると，$$y'=UAV^{ \dagger }x'=\mit\Sigma x'$$にできることを述べている．

 ■特異値分解の手法

実行列$${A(m\times n)}$$に対して，$${AA^{T } }$$や$${A^{T}A}$$ を作ると，これらは，それぞれ$${m}$$次，$${n}$$次の実対称行列になる．この実対称行列に関する固有値問題を考えよう．行列$${A(m\times n)}$$のランクは$${r=rank(A)}$$であるから，$${rank(AA^{T})=rank(A^{T}A)=r}$$である．従って，これらの実対称行列は$${r}$$個の固有値とそれらに対応する固有ベクトルを持つ．異なる固有値に属する固有ベクトルは互いに直交することが知られている．

 実対称行列$$AA^{T}$$と$$A^{T}A$$を考える：

$$ AA^{T}=U^{T}\mit\Sigma VV^{T}\mit\Sigma^{T}U=U^{T}\mit\Sigma ^{2}U $$，$$ \because \Sigma \Sigma^{T}=\Sigma ^{2}(m×m) $$

$${(AA^{T})U^{T}=U^{T}\mit\Sigma^{2 } }$$，$$AA^{T}$$の固有値は；$$\sigma _{1}^{2}, \sigma _{2}^{2}, \cdots , \sigma _{r}^{2}$$

固有ベクトルは，$$U^{T}(m \times m)=\left( \begin{array}{@{\,} c @{\, } }
u_{1} \\[0mm]
u_{2} \\[0mm]
\vdots \\[0mm]
u_{r} \\[0mm]
\vdots
\end{array} \right) $$

$$A^{T}A=V^{T}\Sigma^{T}UU^{T}\Sigma V=V^{T}\Sigma ^{2}V$$,      $$ \because \Sigma^{T}\Sigma =\Sigma ^{2}(n×n)$$

$${(A^{T}A)V^{T}=V^{T}\mit\Sigma^{2 } }$$，$$A^{T}A$$の固有値は；$$\sigma _{1}^{2}, \sigma _{2}^{2}, \cdots , \sigma _{r}^{2}$$

固有ベクトルは，$$V^{T}(n \times n)=\left( \begin{array}{@{\,} c @{\, } }
v_{1} \\[0mm]
v_{2} \\[0mm]
\vdots \\[0mm]
v_{r} \\[0mm]
\vdots
\end{array} \right) $$

 このようにして，$${A}$$の特異値$${\sigma _{1}, \sigma _{2}, \cdots , \sigma _{r } }$$や，特異値ベクトル$${U^{T},　V^{T } }$$を求めることができる．

 ■特異値分解の応用

$$ A=U^{T}\Sigma V=\left( \begin{array}{@{\,} c @{\, } } u_{1} \\[0mm] u_{2} \\[0mm] \vdots \\[0mm] u_{r} \\[0mm] 0 \end{array} \right) \left( \begin{array}{@{\,} ccccc @{\, } } \sigma _{1} & & & & 0 \\[0mm] & \sigma _{2} & & & \\[0mm] & & \ddots & & \\[0mm] & & & \sigma _{r} & \\[0mm] 0 & & & & 0 \end{array} \right) \left( \begin{array}{@{\,} ccccc @{\, } } v_{1} & v_{2} & \cdots & v_{r} & 0 \end{array} \right) = $$

$$=\left( \begin{array}{@{\,} ccccc @{\, } }
\sigma _{1}u_{11} & \sigma _{2}u_{12} & \cdots & \sigma _{r}u_{1r} & 0 \\[0mm]
\sigma _{1}u_{21} & \sigma _{2}u_{22} & \cdots & \sigma _{r}u_{2r} & \\[0mm]
\vdots & \vdots & & \vdots & \\[0mm]
\sigma _{1}u_{r1} & \sigma _{2}u_{r2} & \cdots & \sigma _{r}u_{rr} & \\[0mm]
0 & & & & 0
\end{array} \right) \left( \begin{array}{@{\,} ccccc @{\, } }
v_{11} & v_{21} & \cdots & v_{r1} & 0 \\[0mm]
v_{12} & v_{22} & \cdots & v_{r2} & \\[0mm]
\vdots & \vdots & & \vdots & \\[0mm]
v_{1r} & v_{2r} & \cdots & v_{rr} & \\[0mm]
0 & & & & 0
\end{array} \right) =$$

$$=\sigma _{1}\left( \begin{array}{@{\,} ccccc @{\, } }
u_{11}v_{11} & u_{11}v_{21} & \cdots & u_{11}v_{r1} & 0 \\[0mm]
u_{21}v_{11} & u_{21}v_{21} & \cdots & u_{21}v_{r1} & \\[0mm]
\vdots & \vdots & & \vdots & \\[0mm]
u_{r1}v_{11} & u_{r1}v_{21} & \cdots & u_{r1}v_{r1} & \\[0mm]
0 & & & & 0
\end{array} \right) +\sigma _{2}\left( \begin{array}{@{\,} ccccc @{\, } }
u_{12}v_{12} & u_{12}v_{22} & \cdots & u_{12}v_{r2} & 0 \\[0mm]
u_{22}v_{12} & u_{22}v_{22} & \cdots & u_{22}v_{r2} & \\[0mm]
\vdots & \vdots & & \vdots & \\[0mm]
u_{r1}v_{12} & u_{r2}v_{22} & \cdots & u_{r2}v_{r2} & \\[0mm]
0 & & & & 0
\end{array} \right) + \cdots +\sigma _{r}\left( \begin{array}{@{\,} ccccc @{\, } }
u_{1r}v_{1r} & u_{1r}v_{2r} & \cdots & u_{1r}v_{rr_{ } } & 0 \\[0mm]
u_{2r}v_{1r} & u_{2r}v_{2r} & \cdots & u_{2r}v_{rr} & \\[0mm]
\vdots & \vdots & & \vdots & \\[0mm]
u_{rr}v_{1r} & u_{rr}v_{2r} & \cdots & u_{rr}v_{rr} & \\[0mm]
0 & & & & 0
\end{array} \right) $$

ここで，特異値は大きい順$${\sigma_1\geq\sigma_2\geq\cdots\geq\sigma_r >0}$$に並べてあるので，この展開は良い近似になる．例えば，$${A}$$を画像データとすると，最大の特異値$${\sigma_1}$$に関する行列だけ用いる情報圧縮（次元圧縮）ができる．

ベクトル$$U^{T}(m \times m)=\left( \begin{array}{@{\,} c @{\, } }
u_{1} \\[0mm]
u_{2} \\[0mm]
\vdots \\[0mm]
u_{r} \\[0mm]
\vdots
\end{array} \right) $$や$$V^{T}(n \times n)=\left( \begin{array}{@{\,} c @{\, } }
v_{1} \\[0mm]
v_{2} \\[0mm]
\vdots \\[0mm]
v_{r} \\[0mm]
\vdots
\end{array} \right) $$などは固有ベクトルであるので，それぞれの空間で互いに直交しているが，ベクトル$$u_i$$や$${u_j}$$は，互いに直交しているわけではない．

 
■最小2乗法
既知の実数行列$$A(m×n)$$と$$b(m×1)$$に対して，
$$||Ax-b||^{2}=(Ax-b)’(Ax-b)$$を最小にする$$x$$を求める．
特異値分解ができたら；$$UAV'=\Sigma$$，$$A=U'\Sigma V$$が成立している．
（$$A$$は実行列なので，$$U，V$$は直交行列となり$$U'＝U^{-1}$$などの性質がある．）
最小2乗法は，$$||\Sigma Vx-Ub||^{2}$$を最小にする$$x(n×1)$$を求める課題になる．
$$\textrm{rank}(A)=r≦n<m$$とする．$$\Sigma (m×n), V(n×n), U(m×m)，x(n×1)$$の型であった．

$$r=n$$の場合を考える．

$$\mit\Sigma \equiv \left[ \begin{array}{@{\,} c @{\, } }
\mit\Sigma _{n \times n} \\[0mm]
O_{m-n \times n}
\end{array} \right] $$,　$$V \equiv \left[ \begin{array}{@{\,} c @{\, } }
V_{n \times n}
\end{array} \right] $$の型であるから，
$$\mit\Sigma Vx=\left[ \begin{array}{@{\,} c @{\, } }
\mit\Sigma _{n \times n}V_{n \times n} \\[0mm]
O_{m-n \times n}
\end{array} \right] \left[ \begin{array}{@{\,} c @{\, } }
x_{1} \\[0mm]
x_{2} \\[0mm]
\vdots \\[0mm]
x_{n}
\end{array} \right] =\left[ \begin{array}{@{\,} c @{\, } }
c_{n} \\[0mm]
O_{m-n}
\end{array} \right] $$
一方， 
$$Ub=\left[ \begin{array}{@{\,} c @{\, } }
a_{n} \\[0mm]
a_{m-n}
\end{array} \right] $$
従って，$$ \parallel \mit\Sigma Vx-Ub \parallel ^{2}= \parallel \left[ \begin{array}{@{\,} c @{\, } } c_{n}-a_{n} \\[0mm] -a_{m-n} \end{array} \right] \parallel ^{2} = \parallel c_{n}-a_{n} \parallel ^{2} + \parallel a_{m-n} \parallel ^{2} $$
特異値分解の結果を用いると，第1項は0になり，第２項は残差の２乗を与える，

$$ \mit\Sigma _{n \times n}V_{n \times n}\left[ \begin{array}{@{\,} c @{\, } } x_{1} \\[0mm] x_{2} \\[0mm] \vdots \\[0mm] x_{n} \end{array} \right] = \left[ \begin{array}{@{\,} c @{\, } } a_{1} \\[0mm] a_{2} \\[0mm] \vdots \\[0mm] a_{n} \end{array} \right] $$を解いて$$\left[ \begin{array}{@{\,} c @{\, } }
x_{1} \\[0mm]
x_{2} \\[0mm]
\vdots \\[0mm]
x_{n}
\end{array} \right] $$を得る．