第1回：周期的空間

■第1回：周期的空間(2017.06.28)

無限に広がる平面が，1枚のタイル（平行4辺形）を敷き詰めてタイル張りされている状態を考えましょう．辺と辺，頂点を合わせたタイル張りです．
この平面は，タイルを単位胞としてデジタル化された平面といえます．平面のデジタル化により，連続・等方的であった平面に，周期と異方性が生じています．周期的なデジタル空間は結晶空間と呼ばれます．
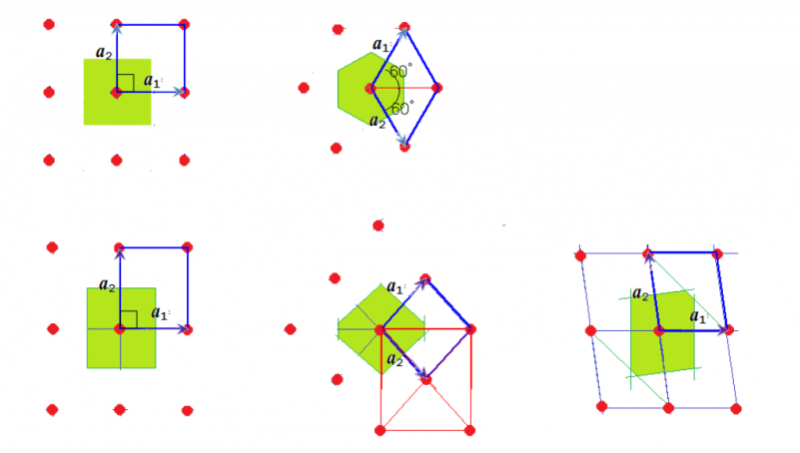
平行4辺形タイルの2辺は，周期的な2次元世界を張る基本並進ベクトル で，これらの整数係数の線形結合 も並進ベクトルです．並進ベクトルの集合全体のイメージは格子（すべての格子点は同値）です．
（注）2次元だから，互いに独立なベクトルは2本あります．平行6辺形でも平面のタイル張りができますが，対向する２辺間の移動ベクトル3種のうち，互いに独立なものは２つのみです．
対象とする単位胞タイルは，平行移動（並進）だけでタイル張りができるものです．従って，3角形や5角形のタイルは使えません．また，ペンローズのタイル張りのような非周期のタイル張りも対象にしません．
並進ベクトルの集合は，加法で群をなし，これを並進群（無限群）Tと呼びます．
並進群を対称性で分類したものがブラベー格子で，2次元では５種類，3次元では14種類，4次元では74種類のブラベー格子があります．
ブラベー格子を直観的に理解するには，デリクレ（ウイグナー＝ザイツ）胞を示すのが良いようです．デリクレ胞とは，１つの格子点に注目し，その格子点と周囲の隣接する格子点を結び，その垂直2等分面で囲んだ胞（あるいは，タイル）です．デリクレ胞は，内部に格子点を1つだけ含み，胞の形の対称性が，このデリクレ胞で張り詰められた無限に続く空間の対称性と同じであることは，自明でしょう．

紙面制限のため，2次元の話にとどめましたが，3次元，さらに高次元の空間でも同様です．この節を終わるにあたり，私の作ったエッシャー様モチーフ「ハロウイン魔女」を鑑賞ください．