
数学月間の会SGKのURLは,https://sgk2005.org/


数学月間の会SGKのURLは,https://sgk2005.org/
■第3回:結晶空間群(2017.12.12)
このシリーズのメインテーマです.結晶空間群Φは,並進群Tを点群Gで拡大して得られます.
逆の言い方をすると,並進群Tは空間群Φの中で正規部分群なので,Tを核とする準同型写像で,空間群Φは点群Gに準同型Φ/Γ=G になります.並進群Tと点群Gとによる拡大の仕方は,(1)点群Gも空間群Φの正規部分群である場合には“直積”,(2)点群Gが非正規部分群である場合は“半直積”です.また,(3)以下に述べる拡張した点群Gとの積の場合は“条件積”と呼ばれます.
空間群の中に現れる点群Gは純粋な点群だけでなく拡張できます.点群Gの中の位数nの演算gはn回繰り返すと gn=1ですが,空間群の中では格子分だけ移動しも同値ですから,(gα)n=1(modT)と拡張できます.つまり拡張された点群には,”映進”や ”らせん軸(3次元の場合)”演算があります.演算gαを含む拡張された点群Gで拡大して得た空間群はnon-symmorphic非共型,純粋な点群Gで拡大して得た空間群はsymmorphic共型と言います.3次元の結晶空間群230種のうち157種,2次元の壁紙模様17種のうち4種がnon-symmorphicです.
◆平面群の作り方(図)
点群G=2mmと,単純長方形格子T=orthoPから,平面群P2mm.P2gm,P2ggの3つが生じます.
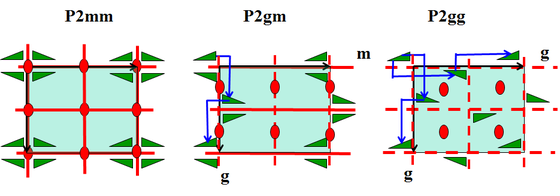
映進gは2回続けると1格子分の移動になるg2=1(modT)ので,格子点はすべて同値という見方をすると平面群 P2mm,P2gm,P2ggは,点群2mmに準同型に還元されます.