数学月間企画講演の第3回は,12月26日(土),15:00-17:00に,27名の参加で実施しました.
この1年間は直接の会合ができず,物足りなさの残る年度でした.とくに,インターネットをやらない会員各位にはご不便をおかけします.ここに年度後半の概要を報告いたしますのでご利用ください.なお,内容詳細は,NPO数学月間の会HPの記事,および,そこにあるリンクからyoutubeに公開した講演動画をご覧ください.
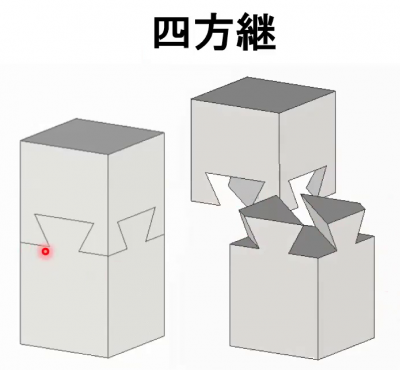
■企画講演(第3回)3Dジグソーパズルのデザインと数学,手嶋吉法(千葉工大)
3D ジグソーパズルとは立体ジグソーパズルのことですが,市販されている地球儀ジグソーなどは,球表面の地図ですので,2Dジグソーになり,3Dジグソーではありません.3Dジグソーパズルの起源は,2000年の池上裕司氏(理研,機械設計)の発明だそうです.講演者もこの直後に理研に在籍し池上氏とともに研究しました.現在も大学で研究テーマの一つとしておられるとのことです.今回の講演内容は,町屋佑季氏(修士論文)の研究に関わります.3Dジグソーパズルは,ピースが全部ばらばらに分解できるものでなければなりません.例えば,3×3×3 のジグソーパズルは,ばらならになる27個のピースよりなります.
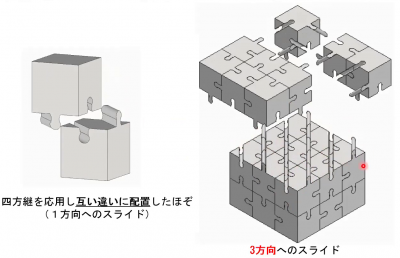
3D ジグソーパズルのヒントは,日本の伝統的な継手(柱を繋ぐ技術)「四方継」にあります.池上式3D ジグソーパズルは「四方繋」を応用して作られました.ジグソーの仕組みをみると,「溝」と「ほぞ」は,常にかみ合っているわけですから,このかみ合わせ部分を1本のパイプで表現すると,ジグソーパズルの構造は空間のパイプの組み合わせとしてモデル化できます.
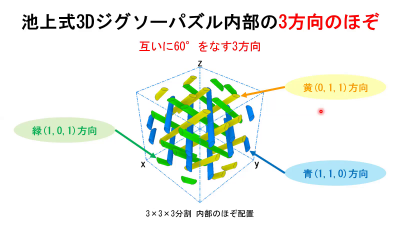
上図のような,無限に伸びたパイプの組み合わせで作られた周期的な構造は,その対称性を空間群で記述できます.この構造例では,空間群は$$Im\bar{3}m$$ で,ジグソー立方体の点群は $$m\bar{3}m$$であろうと推察されます.
町屋佑季氏は,作った3×3×3,4×4×4,5×5×5などの各3Dジグソーパズルを分解し,それぞれを構成するピースの形の種類と個数を分類し報告しています.これらの結果を,立方体内のサイト・シンメトリーとその同価ピースの個数という視点で再検討すると,非常に興味深い知見が得られると思います.