https://elementy.ru/nauchno-populyarnaya_biblioteka/435720/Pryamoe_na_krivom_ili_Progulki_po_iskrivlyonnoy_poverkhnosti
ヴァレリア・シロタ「Kvantik」No.8,2020
まっすぐで平らな道なら、どこでも曲がらずにまっすぐ進むのは容易です。または、広い平原で、遠くにゴールやランドマークが見えればまっすぐ進めます。もし、途中に丘や渓谷があり、さらに、霧や、真っ暗だったりした場合はどうでしょう?どこにまっすぐ行くのか、どうすればわかるでしょう?曲がりくねった山道を歩いているときに「直線に沿って歩く」とは何でしょうか?そして、この坂道を振り向かずに進んでいくと、どこにたどり着くのでしょうか?
そのような疑問にも対応できるようにしていきたいと思います。まずは直線(普通の平面上)とは何かということから始めましょう。次の定義が一番良さそうです。
平面上の直線とは、その2つの点を結ぶ最短経路です。
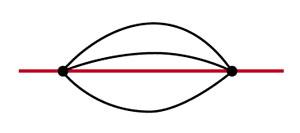
(図1)直線上の任意の2点を取ります。 ある点から別の点に可能なすべての線を描きましょう。 直線上の線分は、これらすべての線の中で最も短いものになります.
この定義は、「まっすぐ進む」という指示に合います。ゴールが直線上にある場合は常に、これがその直線で最短経路です。確かに、ゴールがあなたの直線上にない場合、あなたはそれに到達することは決してありません...
(図2)破線
演習1.(図2)が直線ではないことを証明しなさい。
この演習から、私たちの定義では「どこでも曲がれない」ことがわかります。急に曲がると破線になり、これは最短経路ではありません。
演習2.科学者のシギムントは特定の線を研究し、それが直線であることを証明したいと考えています。彼はすでに、この線に沿った点Aから点Dへの 経路が最短であることを証明することができました 。点BとCがAとDの間のこの線上にある場合、この線に沿ったBからCへのパスも最短であることを証明しなさい。
演習3.科学者マクシミリアンは、点A、B、Cが乗っている別の線を調べ ます。彼は、この線に沿ったAからBへの経路が最短であり、BからCへの線に沿った経路も最短であることをすでに証明しています。これは、この線に沿ったAからCへのパスも最短であることを意味しますか、それともまだ証明すべきことがありますか?
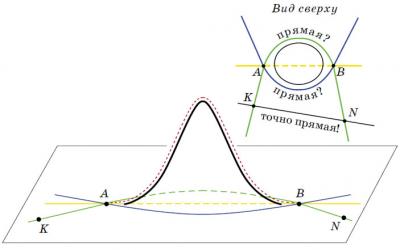
平面上の直線はわかりました。では、この定義を曲面に当てはめてみましょう。例えば、非常に急峻で高い山があるとします(図3)。A地点からB地点までの最短経路は? 確かに山上を通るものではありません。最短の道は、図中の緑の線が示すように、明らかに山の麓のどこかを通っています。演習2で見たように、この線上のAとBの間にある点のペアについても、最短経路の条件が成り立つなら、これが直線でしょうか? さらに、山が対称で、点Aと点Bが厳密に異なる辺にあるとすると、このような最短経路は2つあり、どっちも直線なのですね!?
(図 3)急峻な山。 点Aから点Bへの最短経路は何ですか?
大体そのような考えで良いのですが、しかし、1つの問題があります。ポイントAと Bを超えてこれらの「直線」の延長を正しく描画する方法は? これらの延長は平坦な地形で実行され、すでに「実際の」直線の線分のように見えます。ただし、「直線」に切れ目があってはならないことを覚えています(演習1を参照)。切れ目付近では、「最短経路」条件に違反します。したがって、Aと Bを通過する緑色の「直線」の「端」は、空間内の点Aと Bを通過する直線の非常に先の遠方です (これは、説明した表面上にはありません!)。
そして、ここで問題が発生します:山の周りから遠ざかれば、直線が山の周りをまわる必要はありません。 図3の点Kから点Nまでの最短経路は別の直線になります。
さて、直線の定義は間違っていましたか?それとも、山岳地帯に拡張することは不可能ですか?いいえ、それほどひどい違いではありません:少し修正が必要なだけです。結局のところ、どんな曲面でも、その小さな部分を見ればすべてが小さな平面と見なせます。
「すべてをまっすぐに、まっすぐに」するには、遠くのゴールではなく、一歩先のゴールを見続けなければなりません。そうすれば、表面の曲率には気づかず、次の一歩を前の一歩と同じ方向に踏み出すことになります。そして、あなたが通った道の一つ一つの小片がまっすぐになります。結局のところ、そのすべての小さな部分の曲面は平面のように見えます。
したがって、曲面の場合の直線の定義では、2つの単語を追加します。直線に沿ったパスは、2つの十分に近い点に対して最短である必要があります。これですべてが整いました。この例の点KとNのペアは、十分に接近していないため、考慮できなくなりました。
これらの曲線を直線と呼ぶのは何か気が咎めるので、測地線という呼び方があります。これは、直線の概念を曲面の場合に一般化したものです。
曲面上の測地線は、その十分に小さい部分が、この曲面上の両端間で最短経路になるような線です。
それほど厳密ではありませんが、測地線は、すべての小さな(ほぼ平坦な)部分上で直線のように見える曲線です。
ちなみに、対称的な山の例では、描画した2つの測地線に加えて、第3の測地線が点Aと Bを通過し ます。これは、最初に最短ではないと拒否した山の頂上を通るパスです。これで、点AとBが十分に接近していないと宣言できます。
ご覧のとおり、ユークリッドの公理は、任意の2点(平面)を通る直線を1本だけ引くことができるというものですが、曲面の測地線ではまったく機能しません。たぶん、AとBを通る「直線」はもっと引けるかもしれません。山の形によりますが。
また、図3の緑と青の線のように、現実には「まっすぐ」な道(すなわち測地線)が、地図上では「曲がっている」ように見えることもあることを覚えておくと便利です。
***
これで、どような地形でも「まっすぐ進み、曲がらない」とはどういう意味かがわかりました。これは測地線に沿った動きです。今、どんな表面に対しても、次の質問をすることができます:
1.その測地線はどのように見えますか?
2.2つの与えられた点を通る測地線を描くには?
一般的な場合、この問題は難しいので、円柱と円錐という単純な「ほぼ平坦な」表面を歩くことを提案します。
シリンダー
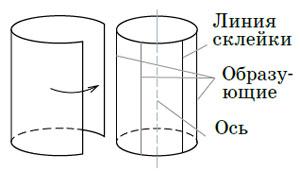
図4: シリンダー
シリンダーを作るのは簡単です(図4):紙を1枚取り、それを筒に巻き、端を接着します(できれば長辺に沿って)。カブトムシをその上に乗せて、それが這うように測地線を描くことができます。
最初から接着線に平行な方向を選択すると、カブトムシはこの線(および円柱の軸)に平行な直線に沿って這うようになります。このようなラインはジェネレーターと呼ばれます。軸に垂直な方向に移動を開始すると、測地線は円になります。
チャレンジ問題 斜めなど、他の方向に進むと、どのような線が表示されますか?
円錐
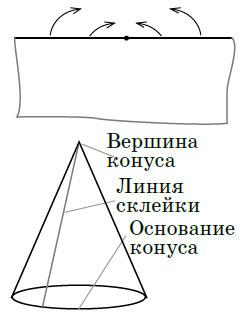
図5 円錐
すぐ作れます。接着も簡単です。最も簡単な方法は、大きな紙を取り、その側面の1つの点を選択し、この点で区切られた側面の2つの半分を接着することです(図5)。円錐の底面が不均一で、角が突き出ていても問題はありません。実際の円錐面は無限であり、これはほんの一部であると見なすことができます。
問題 この表面で測地線はどのように見えますか?
---続く