投稿日時: 2020/10/05
 システム管理者
システム管理者
18/19学年度のクバンチク数学コンテストなどの問題より
3つ選びました.挑戦してみましょう.
■雑誌エレメント2020.9より改題
平方数A_n(n=1,2,3,4,5,6・・・・)とは;1,4,9,16,25,36,・・・・・
(一辺nの正方形の中に直径1の円を並べたとき入る円の数)
3角数B_m(m=1,2,3,4,5,6,・・・)とは;1,3,6,10,15,21,・・・・・
(一辺nの正3角形の中に直径1の円を並べたとき入る円の数)
平方数でもあり3角数でもある数を求めなさい.無限にありますがいくつ求められますか.
ヒント)A_n=n^2 ,B_m=m(m+1)/2 です.
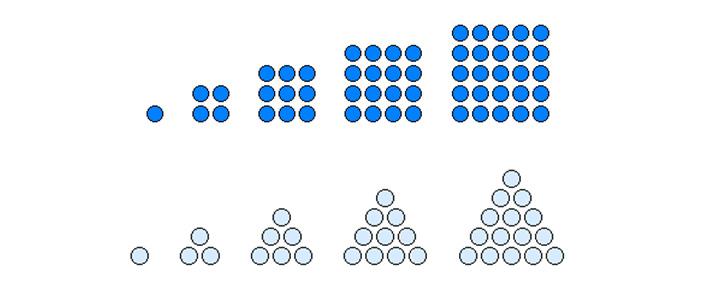
■7ラウンド問題34より
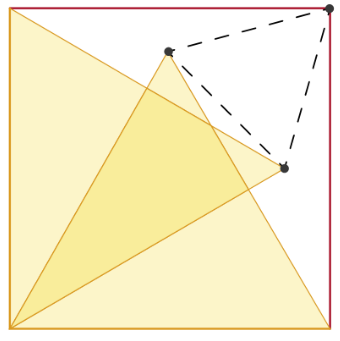
図に示すように,2つの黄色の等辺三角形が正方形に配置されています.マークされた3つのポイントが等辺の三角形を形成していることを証明しなさい.
■4ラウンド問題20(エゴールバカエフ)より
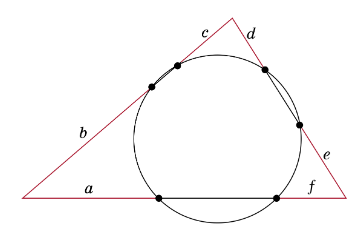
円は三角形の辺と6点で交差します(図を参照).
a)a = bおよびc = dの場合,e = fであることを証明しなさい.
b)b = cおよびd = eの場合,f = aであることを証明しなさい.