Максим Прасолов(マクシム・プラソロフ)による«Квантик» №12, 2020の記事の図を利用しました.
加工した図もあります.文章は原文と異なります.理解し易いように要約して書き直しました.
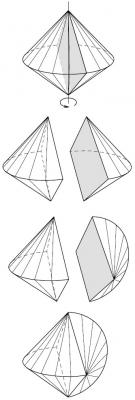
テトラコーンの作り方
ソロバン球のような形(双円錐)を,上下の頂点を通る平面で2分割したときの断面が正方形であるような双円錐から始めます.2分割した双円錐の片側の部分を90°回転して張り合わせて作った図形がテトラコーンです.このような貼り合わせができるのは,断面が正方形だからです.
■テトラコーンは4つの半円錐の側面からできていて,
この立体の対称性(点群)は$${\tilde{4}mm}$$です.
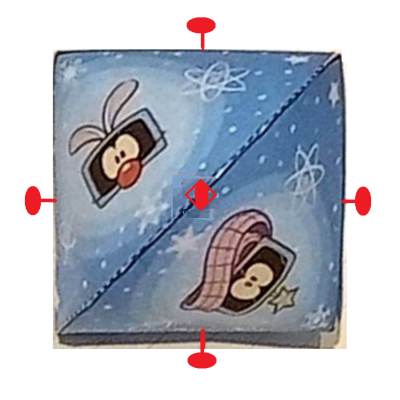
作製したテトラコーンの写真
糊代が立体内部にあるので,組み立てにテクニックを要する.
作ったテトラコーンを展開図の上で転がしてみましょう.
テトラコーンの4つの半円錐側面は,面を接してこの展開図の上を転がることは明らかです.テトラコーンが転がるとき,次の性質があります:
(1)テトラコーンの中心の描く軌跡はどのようなものでしょうか.
(2)テトラコーンの中心は,紙面から一定の高さ(変動しない)を保つ.
(3)しかし,テトラコーンは定幅立体ではない.
(注)ルーローの3角形は,定幅図形であるが,中心位置は変動する.
■ポリコーンに一般化
この性質をもつ立体を一般化しポリコーンを作ることができます.
テトラコーンの断面は正方形だったが,断面正6角形から得られるのはヘキサコーン,断面正8角形から得られるのはオクタコーンです.一般に,偶数の正多角形からポリコーンを作ることができるが,奇数の正多角形からはポリコーンを作ることはできません.
ポリコーン作りの説明は,Максим Прасолов(マクシム・プラソロフ)による«Квантик» №12, 2020の記事では,冗長で理解しにくい.
以下に掲載するYouTube動画を観察すれば,自然に理解できると思います.
https://youtu.be/R27xHl_joRw
この動画はDavid Hirschによるが,テトラコーンは1980年にDavid Hirschによって特許取得がされた.
面白い性質を持つこのような立体が,何に役立つのだろうか?いろいろな使われ方が将来出て来ると思いますが,分かり易い例を示すと,ダンサーのフランツィスカ ハウザーのウエブサイトが興味深い.この記事の表紙写真は,彼女のウエブサイトから借用しました.そこでは,八面体の湾曲したエッジで構成された台が使用されている.2つのエッジは,テトラコーンの半円2つ,残りは内側に曲がっている構造で必要なエッジです.
https://www.zirkus-meer.at/artisten/franziska-hauser/
Franziska Hauser - Zirkus Meer www.zirkus-meer.at
フランツィスカ ハウザーのウエブサイトより