ユーリ・マルケロフ「kvantik」# 3、2019の図を引用しますが、設問は変更しました。
図:1
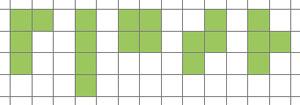
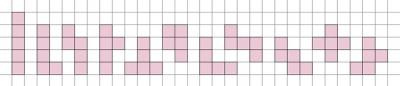
ポリオミノとは、何個かの正方形セルを側面に接合した形状です。たとえば、テトラミノは4つのセルのポリオミノであり、形状は5種類あります(図1)。5つのセルからなるポリオミノはペンタミノと呼ばれ、12種類の異なる形状があります(図2)。
Q1.図2には1つのペンタミノが抜け落ちていますが、どんな形が抜けているかわかりますか.
図:2
テトラミノのある1種類を選び、選択した種類のテトラミノのみを使用して、以下の図形を作成してください?(テトラミノは裏返すことができます。)
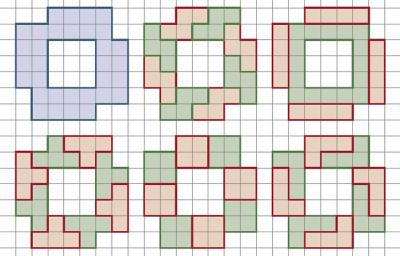
答えを図3に示します。
図:3
ペンタミノについても同じ質問をしましょう。ここでは状況が異なることがわかります。
ペンタミノのタイプを選択して、選択したタイプのペンタミノのみを使用して、作成できるような有限の図形はありません。
何故でしょう?
問題がわかりにくいので、この問題を私は次のような設問に変更します:
Q2.ある有限図形があって,12種類あるペンタミノの任意の1種類を選択して,そのペンタミノのみでその形を分割できるとする.
そのような有限図形はありますが?
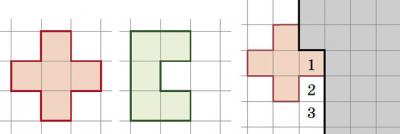
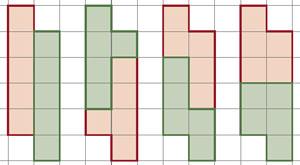
Q3.十字架(図4)だけ,あるいは,アーチ(図5)だけに「分割」できる有限の図形が存在しないことを証明してください。
図:4、 図:5、 図:6
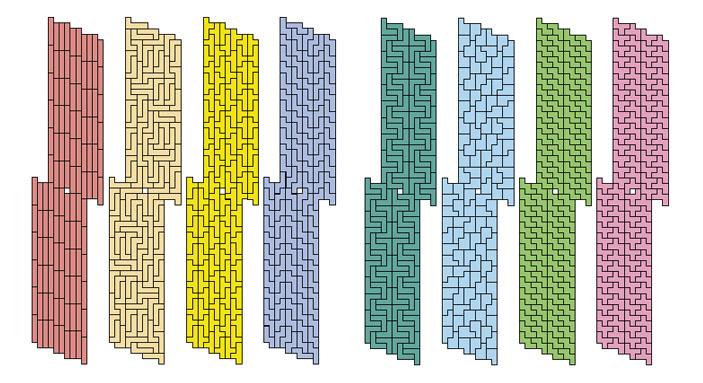
図:7
図7の例は、ある図形の4種類の分割例です。残りの8種類のペンタミノのうちの1種類を使ってこの有限図形の2分割はできません.
GeorgeSichermanが発明した図は、8種類のペンタミノに分けることができます。
ポリオミノや他の図に関する多くの興味深い問題や写真は、recmath.orgで見つけることができます。
アーティストArtyomKostyukevich