https://book.etudes.ru/articles/crystallography/
Николай Петрович Долбилин
2011 年のノーベル化学賞は「準結晶の発見」に対して授与されました。これは、これまで見られなかった原子の配列構造を持つ固体です。この発見により、固体の研究に新しいページが開かれました。固体は、結晶とアモルファス構造(ガラス、プラスチック)の2つのタイプに分けられます。古代に注目された結晶と非晶質体の違いは、結晶には天然のファセットがあることで、それは、たとえば砂糖や塩の小さな粒など、ミクロレベルで明確に現れることがあります。自然科学者は、結晶の自然なファセットは、その内部構造によるものとしました。
物質の性質は化学組成だけでなく、原子(分子)の並び方によっても決まり、物質の構造を知ることは重要です。よく知られている例は、グラファイトとダイヤモンドで、化学的には同じ、どちらも炭素です。しかし、これらの炭素の配列構造は完全に異なり、結晶群も異なります。その結果、これらの素材は異なる物理的特性を持ちます。非常に柔らかいもの、非常に硬いもの、つや消しの黒、透明なものなどです。
結晶の構造と結晶形成の問題を研究する科学は、結晶学と呼ばれます。準結晶の発見後、これらの新しい構造の研究に特化したセクションが登場しました。
結晶クリスタルという言葉は古代ギリシャ語κρύσταλλοςに由来し、「氷」、「山の氷」または「水晶」を意味します。
科学の別の要素は、ある程度結晶学に起因する可能性があり、古代ギリシャ人の作品 (正多面体) に見られます。I. 17 世紀初頭 (1611 年) に登場したケプラーの論文「六角形の雪片について」は、構造結晶学に関する文献の最初の先駆者と見なされています。フランスの著名な科学者 R. J. ハユイによって表現された「劈開面」に関する結晶学の最も重要な命題が策定されたのは、18 世紀末になってからのことです。この発見の歴史は、「ニュートンのリンゴ」の伝説に似ています。方解石の結晶は、Guyuy の手からの偶発的な落下によって多数の菱面体の破片に粉砕されました。これにより、結晶は平面に沿ってのみ分割できるという考えが生まれました。その方向は、この結晶によってあらかじめ決定されています。破片をさらに粉砕すると、結晶が平行六面体と平行六面体に組み合わせることができるような形状の多面体で構成されていることが示されました。
互いに結合した平行六面体のセットとしての結晶の平行六面体構造の概念から、結晶格子の理論が発展しました。この理論の作成者は、最大の結晶学者の 1 人である O. Brave でした。
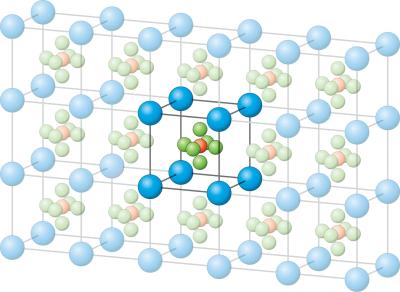
3 つの非同一平面上にある (同じ平面にない) ベクトルを構築します。、 、 平行六面体を変換 (シフト) してベクトルに分割するここで係数、 、 - 整数。こうして得られた平行六面体の頂点の集合が格子である。物質の原子を表すいくつかの点が最初の平行六面体に配置されている場合、考慮される「複製」では、いくつかの平行に配向された格子のファミリが得られます。同一の平行な格子のこの組み合わせは、19 世紀前半に登場した結晶の数学モデルであり、一般的にいまだに「機能」しています。直線的に独立した 3 つの方向における結晶の内部構造の周期性は、結晶学の主な原理です。
すべての結晶学の中心的な数学的アイデアは、結晶の対称性です。図形の対称性は、図形とそれ自体を組み合わせた空間の動きです。任意の図形のすべての対称性の集合には、次の 3 つの特性があります。
1) 2 つの対称性の積それらの順次実行の結果として、図の対称性もあります。
2) 空間内の任意の点をその場に残し、したがって任意の図形を不動のままにする、いわゆる同一の動きも、図形の対称性と見なすことができます (実際、同一の動きは動きではなく、「立っている」ことです)。場所);
3) 対称性とともに反対の動き空間の各点を元の場所に戻すは、図形の対称性でもあります。
これら 3 つのプロパティを持つモーションのセットは、対称グループと呼ばれます。
ポイントを取ると対称性のいくつかのグループからのすべての動きで空間を破壊します、次に、軌道と呼ばれる一連の点を取得しますポイントグループに関して.
たとえば、正方形の対称群は 8 つの要素で構成されています。恒等を含む 4 つの回転と、4 つの線についての反射です。また、点の軌道は、この点の選択に応じて、8 つ、4 つ、または 1 つの単一の点 (後者 - この点が正方形の中心である場合) で構成されます。
与えられた図形のすべての対称性のグループとともに、与えられた図形の不完全なグループ、つまり、条件 1) ~ 3) が満たされる完全なグループの対称性のサブセットも考慮されます。
1 つの点が原点と一致する任意の格子を考えます。座標の原点を保存し、同時に格子を結合する空間の運動のグループは、結晶クラス(点結晶グループ)と呼ばれます。Bravais の前でさえ、32 の結晶クラスすべてが発見されました (J.F. Hessel, 1830)。回転の中の結晶クラスでは、2次(180°回転)、3次(120°回転)、4次(90°回転)、6次の軸が存在できることが非常に重要ですが、五次はありえない。
ある格子の完全な点群である結晶クラスは、ホロヘドリーと呼ばれます。格子。32 の結晶クラスのうち、ホロヘドリアは 7 つしかありません。「最も貧弱な」ホロヘドリーは三斜晶系であり、2 つの要素で構成されています。同一の変換と格子点に関する対称性です (任意の格子はそのような対称性を持ちます)。より豊かなホロヘドリア - 単斜晶、直交、正方形、菱面体、立方体、六角形 - はすべてに固有ではなく、特別な格子にのみ固有です。Bravais は、六角形の全面体を含む格子を除いて、他のすべての格子で平行六面体の格子を見つけることができることを発見しました (一般的に言えば、格子が構築された主要なものとは異なります)。その対称群は格子全面体です。 . このタイプの各格子に対して、最小体積の平行六面体が呼び出されますブラヴェの平行六面体。六角形のホロヘドリー (正六角柱の完全な群と一致する) の場合、ブラヴェの平行六面体は特別な方法で定義されます。ブラヴェは、すべての格子に対して平行六面体を発見しました。大きく異なるタイプは 14 であることが判明しました。したがって、グレーティングも 14 のブラヴェ タイプに分散されました。
ブラヴェ分類は、結晶の最も一般的な対称群、いわゆる結晶学的群を記述するための基礎となりました。
空間の運動のグループは、その点のいずれかの軌道が離散セット、つまり点が互いに分離されている場合、結晶学的と呼ばれます。さらに、そのようなグループに関する軌道は、仮定により、任意に大きな空洞を持つべきではありません。十分に大きな固定半径のボールが配置されている場合は、指定された軌道からの少なくとも 1 つのポイントが含まれている必要があります。
最も単純な結晶学的グループの例は、次のグループです。 、非共平面ベクトルによる 3 つのシフトによって生成されます、 、 . このいわゆる最初の三斜グループは、格子ベクトルへの空間の変換で構成されています. 軌道であることは明らかである.任意の点格子からこの格子自体があります。したがって、最初の三斜群は格子の対称群です。イフポイント格子に属さない場合、軌道平行移動によって元の格子から得られる別の格子があります。最初の三斜グループに関する軌道は離散セット (この場合は格子) であり、十分に大きな半径の各ボールには格子からの少なくとも 1 つの点が含まれているため、グループは結晶学的です。
平行移動に加えて、格子には他の対称性もあります。したがって、格子の任意の点、および任意の「半整数」点、つまり形式の点に関する空間の対称性
は格子対称です。格子の整数点と半整数点に関する平行移動と対称性のセットは、いわゆる第 2 三斜群を形成します。これは、次に複雑な結晶グループです。最悪の場合、非対称格子では、三斜群が格子の最大対称群です。
もう 1 つのことは、格子が豊富な点対称性 (ホロヘドリー) を持っている場合です。たとえば、立方格子のホロヘドロンは、立方体の完全な対称群と一致します。これは、48 回の回転と反射を伴う回転で構成されます。したがって、立方格子の完全なグループでは、そのポイントの各ペアに対してと 48の動きがあります。立方格子グループは、結晶グループの別の例です。
19 世紀における結晶学の発展の集大成は、偉大なロシアの結晶学者 E. S. Fedorov (1857-1919) の研究でした。彼は、対称群が結晶学的群である離散的な点 (原子) の集合として結晶を定義しました。言い換えれば、Fedorov によれば、結晶は、いくつかの結晶学的グループに関するいくつかの原子の一連の軌道です。.
E. S. Fedorov (ドイツの数学者 A. Schoenflies と同時に) は、1891 年にすべての結晶学的グループを発見し、230 であることが判明しました。この複雑な数学的結果は、結晶の構造とそれらの対称グループに関するその後の詳細な研究の基礎となりました。 .
230 の結晶グループのうち 229 には、並進運動だけでなく、回転要素を伴うより複雑な運動も含まれていることに注意してください。これらのグループには格子対称性が含まれており、Bravais によって得られた分類を使用してそれらを導き出しました。結晶の定義に対する Fedorov のアプローチは、Bravais によれば、結晶のクラスを拡張するように見えました。これは、Bravais によれば、平行に配向された格子 (平行移動のみのグループに対する一連の軌道) の結合です。Fedorov は、3 次元空間で作用する結晶学的グループには、同一平面上にない方向への 3 回の並進によって生成されたサブグループが含まれていると確信していました。この主張は、Schoenflies によって厳密に証明されました。この特性により、フェドロフによると、以前のように、ブラバによると、クリスタルは、
20 世紀の初めに、物理学の分野における顕著な発見のおかげで、結晶の格子構造に関する結晶学の主要な位置が確認されました。1912 年、ドイツの科学者 M. ラウエは、結晶格子上での X 線散乱中に回折を発見しました (1914 年ノーベル賞)。ラウエの発見に基づいて、英国の物理学者 W. L. と W. H. ブラッグ父子は、結晶の X 線回折分析の基礎を開発しました (ノーベル賞、1915 年)。
したがって、フェドロフによる結晶の定義によれば、その内部構造は最も対称性に富んでいます。自然界や地質博物館で天然の結晶を見て、結晶の外形の美しさを直視できるとしたら、内部構造の美しさは、どこかの研究室や大学の学部の模型でしか見ることができません。 . これらの非常に美しい構造は、結晶化の結果として形成されます。つまり、物質が液体の無秩序状態から固体の結晶状態に移行する際に形成されます。このような遷移は、冷却中など、特定の物理的条件下で発生します。結晶化中に全体的な秩序が現れる理由は何ですか?
常識的には、結晶の原子構造の全体的な秩序は、同種の原子の近くでの局所的な配置の繰り返しの結果であると考えられていました。フラグメントのアイデンティティの出現は、物理的な観点からも説明できます。アメリカの物理学者 R. ファインマンは次のように書いています。原子をさらに遠ざけると、まったく同じ条件が再び見つかります。注文は何度も何度も繰り返され、もちろん、すべての3次元で...」. ローカル秩序からのグローバル秩序の起源には確信がありましたが、正確な定式化と証明はありませんでした.
結晶の世界秩序の「局所的原因」に対する信念は、V. A. ステクロフ数学研究所の B. N. Delaunay と彼の幾何学者の学生によって行われた結晶の局所理論に関する研究の結果として得られた定理と証明に取って代わられました。1970 年代に開始された一連の作業で、MIAN の作業者は離散セットの結晶学的基準を証明し、近隣の半径の推定値を見つけ、その同一性が構造の正確性を保証しました。局所理論には、正規システムの局所フラグメントの特性と、それらをグローバルに順序付けられた構造に「組み立てる」ための規則を記述するアプローチが含まれていることにも注意してください。
Boris Nikolaevich Delaunay によって開始された局所理論に関する研究のサイクルは、Delaunay の半世紀にわたる幾何学的結晶学の発展に関する研究の価値ある継続であり、Delaunay 集合論、Delaunay の三角形分割理論などのツールの出現をもたらしました。はるかに。
結晶の局所理論に見られる正確な条件の役割は、離散セットのファミリーから正確に周期的構造を区別し、いわゆるペンローズ パターンの出現で再評価されました。1970 年代に英国の物理学者 R. ペンローズによって発見された平面構造では、一般に周期性はありませんが、局所的なモチーフが何度も繰り返されています。
ペンローズ パターンには、5 次の無限に多くの対称軸が含まれていることが特徴です。直線は、360 ° / 5 の角度でそれらの周りを回転することにより、パターンの一部がそれ自体に入ります。さらに、ペンローズ パターンでは、5 回対称性を持つ任意の大きなフラグメントを見つけることができます。一方で、これらのフラグメント (1 つの例外を除く) は制限する必要があります。その後、数学者は、同様の特性を持つ構造が 3 次元空間にも存在することを示しました。
そのような構造が結晶を表すことができないという事実は、19 世紀には早くも結晶学者に知られている特性から得られたもので、周期構造は 5 次の対称軸を持つことはできません。
幾何学の新しい研究分野、つまり準結晶構造が生まれました。しかし、「本物の」準結晶が存在するかどうかという問題は未解決のままでした。
1982年、イスラエルの物理学者D.シェヒトマンの研究室で、アルミニウムとマンガンの合金が得られました。その構造は、5次の明確な軸対称性を持っていました...30年後、この発見はノーベル賞を受賞しました化学の「準結晶の発見に対して」。
結論として、指定された特性を持つ新しい構造を予測する分野で、新しい材料の理論的設計に関する集中的な研究が最近行われていることに注意してください。この方向性は、新しい驚くべき特性を備えた材料の作成を約束します. そして、これらの研究の重要なツールは幾何学的方法です。