この論文を紹介する前に,次のyoutube動画をご覧ください.クラドニ図形は,楽器の音響学にも関係しそうですね.
フョードル・ナザロフ,ミハイル・ソディン,アレクサンドル・ログノフ
「トリニティオプション-サイエンス」第16号(310),2020年8月11日の抄録
ある工場で,複雑な装置が停止してしまい,1人の専門家では何もできませんでした.若い男がやって来て,あらゆる側面から複雑な装置を調べていましたが,普通のハンマーを取りだし装置を一撃すると,装置が作動し始めました.ハンマーで打つことが高い報酬になったのではなく,ハンマーでどこを打つべきかを正確に見極めたところが報酬に値したのです.
似たようなことが最近数学で起こりました.2020年のヨーロッパ数学会の賞であり,数学への卓越した貢献が認められた35歳未満の10人の研究者に4年ごとに授与されます.
ここで対応するのは,
「複雑な装置」⇔「楕円微分方程式の解の節点幾何」,
「ハンマー」⇔中学生が知っている「組み合わせ幾何学的考察」
であり,若者の名前はAlexander Logunovでした.
節点形状の起源は,振動板に注がれた細かい砂が節線に集められ,境界条件の板形状と振動周波数に応じて奇妙なパターンを形成するフックとクラドニの実験に戻ります.これらの線は,静止しているプレート上の点で構成されます.読者は,グーグルで「クラドニ図形」と入力することにより,これらの実験の多数のイラストを見つけるでしょう.
振動から生じる節線についてのさまざまな疑問は,200年以上にわたって科学者を魅了してきました.アレクサンドル・ログノフが受け取った賞は,この分野での最初の賞ではありませんでした.1809年,クラドニがパリを訪問した後,フランス科学アカデミーはコンテストを発表しました.その目的は,「弾性表面の数学的理論を構築し,それが実験データとどの程度一致するかを示すこと」でした.賞はソフィー・ジャーメインが1816年に受賞しました.その数学的モデルは,少し後のグスタ・フキルヒホフによって完成しました.
剛体プレートではなく,柔軟な弾性膜の振動理論は,Logunovの研究が直接関連することに注目ください(違いは,膜が伸張のみに抵抗し,プレートは曲げと圧縮に抵抗するためより複雑な数学モデルになる点です).この場合,膜は任意の形状にでき,固定されたエッジを持つ平面,球状,ドーナツの形など,多次元にすることもできます.
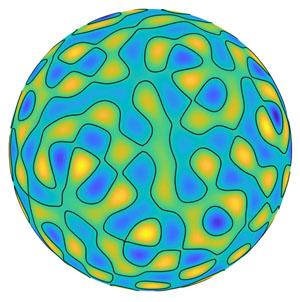
ランダムな球面調和符号
小振動の理論の基本原則の1つによれば,平衡位置からの膜の変位を表す関数は,最も単純な固有振動の重ね合わせとして表されます.各固有振動は特定の周波数ωで発生し,積$$cos(2πωt)v_ω(x)$$によって記述されます.ここで,tは時間,$$v_ω(x)$$はいわゆる固有関数で,膜の点xのみに依存します.
微分方程式の観点から,固有関数$$v_ω$$は方程式$$Δv_ω+4π^2ω^2v_ω= 0$$の解であり,節線(3次元以上)は,条件$$v_ω(x)= 0$$を満たす単純な点xです. ここでの記号Δは,ユビキタス・ラプラス演算子を示します.明示的な式は,選択した座標系と膜の弾性特性によって異なります.
ランダムな球面調和値の分布
通常のデカルト座標で表される平らで均質な膜の場合,膜の形状は$$ \mit\Delta =\displaystyle \frac{ \partial ^{2 } }{ \partial x^{2 } }+\displaystyle \frac{ \partial ^{2 } }{ \partial y^{2 } } $$です.上記のラプラス演算子の固有関数は,幾何学および確率論から量子力学に至るまで,数学および物理学の多くの分野に現れます. したがって,固有関数の振る舞いとそれらの節線は綿密な研究の対象であるのは当然なのですが,今日まで多くの課題が未解決のまま残されています.
どうやら,節点集合の問題の最も有名なものは,40年以上前に表現されたそれらのサイズに関するヤウ シンツン予想でした.彼女は,この次元(2次元の長さ,3次元の領域など)は常に周波数ωの線形関数として成長すると主張しています. 振動膜に追加の対称性がある場合,固有関数が明示的に見つかることがあります.対称性がない場合,固有関数の明示的な式を記述して節点集合のサイズを推定することは不可能です.それらは通常,膜を小さな正方形に分割し,それぞれのサイズを推定して,結果を追加します.
ヘルムホルツ方程式の解の境界点
そのような推定のための便利なツールは,倍加指数$$N(Q)=ln\displaystyle \frac{\textrm{max}_{2Q}|v_{\omega }|}{\textrm{max}_{Q}|v_{\omega }|}$$ であり,立方体Qから立方体2Qに,中心が同じで辺が2倍になると,固有関数の絶対値の最大値がどれだけ速く増加するかの指標です.有用な事実は,倍加指数が有界のままであれば,立方体Qに該当する節点集合のサイズも有界であることです.
ヤウ仮説における最初の重要な進歩は,約30年前にハロルド・ドネリーとチャールズ・フェファーマンによって行われました.彼らは,任意の正方形について固有関数倍加指数が振動周波数によって上から推定されることを証明しました.この一連の問題での次の進歩は,ニコライ・ナジラシビリによります.彼は,ヤウ・シンツンによって提起された質問は,より単純なクラスの調和関数の関連する質問に還元できることに気づきました.これは,方程式Δv= 0の解(膜の定常状態を表します)です.ナジラシビリの質問の中には,たとえば次のようなものがあります.3次元空間の一定でない調和関数が無限領域の集合で消えるのは本当か? (平面上の同様の命題は単純な演習です) 25年間,中心となる数学的対象の1つに関するそのような無邪気な質問が未解決のままでした.
ドンネリ,ヘッフェルマン,ナジラシビリの研究の後,基本的な問題は,正方形(または高次元の立方体)が小さな断片に分割されたときに調和関数の倍加指数がどうなるかであることが明らかになりました.多くの数学者の努力にもかかわらず,2016年にアレクサンドル・ログノフとエフゲニア・マリンニコワの研究が発表されるまで,この問題は進展していませんでした.
これらは,次のエレガントな組み合わせ補題に基づいています(私たちは,すでに主要な問題を含んでいるフラットケースのみに制限しています).調和関数の単位平方に大きな倍加指数Nがあるとします.次に,この正方形を同じサイズの十分に小さい正方形のA^2にカットすると,最大でA / 2で,倍加指数がN / 2を超える可能性があります.この補題は,上記のナジラシビリの仮説とヤウの仮説の一部の証明につながり,少し後に,エッジでクランプされた均一な平膜の自然振動の節線の長さが,周波数の線形関数として増加することを証明しました.
A.スターンの論文からの節曲線
結論として,アレクサンドル・ログノフ自身について一言.アレクサンダーはペルミとサンクトペテルブルクで育ちました.多くのピーターズバーグの数学者と同様に,彼は市内の数学学校の1つを卒業しました(239番目). 2015年,彼はビクトル・ペエトロビッチ・ハビンの指導で博士論文をとりました.テルアビブで2年間過ごした後,アレクサンダーはプリンストンに移り,今日まで働いています.彼は今でも定期的にサンクトペテルブルクとテルアビブの両方を訪れ,他の同様に困難でエキサイティングな課題の解決に成功しています.
「節点形状を実行しています」
プリンストン大学(米国)の助教授であるアレクサンダー・ログノフは,新聞からのいくつかの質問に答えました.
アレクサンドル・ログノフ
-どのようにして数学に入学したのですか?選択について疑問はありましたか?
-私は12歳の男子生徒として、サンクトペテルブルクのPhysics and Mathematics Lyceum No. 239の素晴らしい数学サークルに偶然出会い、私の教育に大きな役割を果たしました。私は、この非常に成功したサークルとオリンピックのシステムとまだ連絡を取り合っています。初年度は、数学と経済学の2つの分野で同時に勉強する許可を得ました。授業が始まってから2週間後、自分が何で何がそうでないかがはっきりとわかりました。
-あなたの数学の興味のある分野をどのように説明しますか?
-分析(不等式の科学)、幾何学、数理物理学。
-人気のある科学形式(私たちは物理学者だけでなく言語学者にも読まれています)で、ヨーロッパ数学会の賞を受賞した結果を説明していただけますか?
-賞のプレゼンテーションでは、それはどこにも言われていません。過去5年間、節点形状を作成してきました。
「節点セット」という用語は、物理学者によって、たとえばクラドニの実験ではっきりと見える驚くべき線を表すために造られました。この実験では、金属板の上に弓が描かれ、それが共振します。
レオナルドダヴィンチ、ガリレオガリレイ、ロバートフックなどの物理学者は、互いに独立して節点集合に注意を払い、エルンストクラドニはそれらを体系的に研究して説明しました。ナポレオンはクラドニの共鳴実験に非常に感銘を受け、フランス科学アカデミーがこの実験の数学的説明の中で最高の賞を受賞するよう提案した。賞が授与された後、フランスの物理学者と数学者は、何の方程式が節点集合を説明するかについて何年もの間議論しました。
1816年、ソフィージェルマン(マリーソフィージェルマン、1776年から1831年)が賞を受賞しました。彼女のおかげで、節点集合は楕円方程式の解の零点であり、数学者はこれを研究して抽象的なレベルで説明しようとしていることを知っています。節点セットに関する数学的質問を簡単に思い付くことができます。物理学者が作成した写真を見て、目に見えるものを証明または反証する必要があるだけです。最も有名な質問は、Yau仮説(Yau Shintunの後)です。これは、節線の長さが周波数にどのように関連しているかを示しています。
D. BelyaevとA. Logunovによる絵。編集者は、親切に提供されたイラストを提供してくれたDmitry Belyaevに感謝します。