爪問題と貴金属数（metallic number）

■貴金属数(metallic number)
貴金属数とは，黄金数（黄金比）を一般化して得られる概念です．
（１）黄金比$$φ＝A/B$$とは，$$(A+B)/A=A/B$$を満たす数値$$φ$$です．

この定義から，$$(φ+1)/φ＝φ$$を解いて，$$φ＝(1+√５)/2=1.618033････$$が得られます．

（２）貴金属数 は，$$n$$個の長いAと1個の短いBに分けて，$$(nA+B)=A/B$$を満たす数値$$A/B=λ_{n}$$のことです．
これが黄金比の拡張であることは，黄金比は$$n=1$$とした$$λ_{1}$$に相当するので納得できます．
（３）貴金属数の$$n=2$$のときは，白銀数$$λ_{2}$$と呼ばれます．$$λ_{2}=1+√2$$になることを各自ご確認ください．

（４）一般化した貴金属数$$λ_{n}$$を求めましょう．
$$λ_{n}=A/B=n+B/A=n+1/λ_{n}$$，すなわち，$$(λ_{n})^{2}=nλ_{n}+1$$，
この2次方程式を解いて，
$$λ_{n}=[n+√(n^{2}+4)]/2$$　となることをお確かめください．

■Gokul Rajiv と Yong Zheng Yewによる「爪問題と貴金属数（metallic number）」というエッセイが，プラスマガジン（10月，2020）に掲載されました．https://plus.maths.org/content/fingernail-problem-and-metallic-numbers

爪問題というのは，爪を切るのに爪切りを使わずハサミ（直線切り）で多角形のように円弧を切ところから名づけられました問題です．
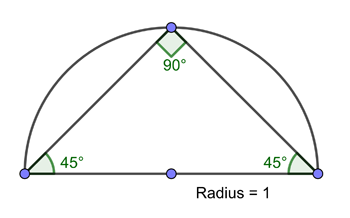
次の図は，半径１の半円弧を長さの等しい2つの線分で表した図です．線分の長さは√2です．

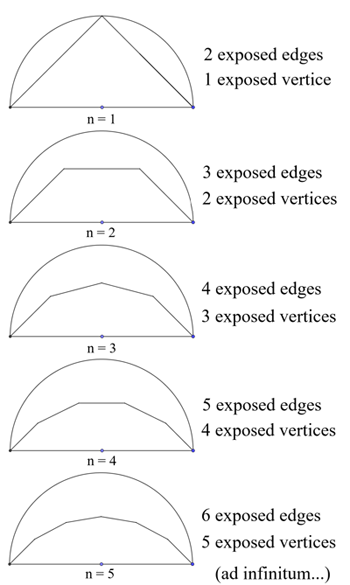
次に，頂点の所を切り落とし，３つの線分の長さを等しくすると，以下の$$n=2$$のときの図になります．同様に，２つの頂点を切り落とし，生じた４つの線分の長さを等しくすると，$$n=3$$のときの図になります．このような操作を繰り返すと一つの円弧に収束していきます．

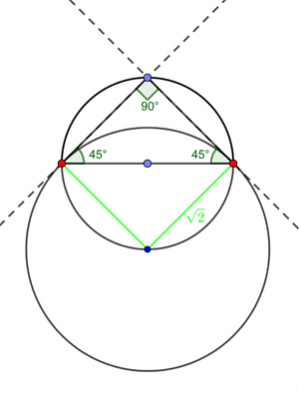
その最終的な円弧は，始めの半径１の円周上に中心のある円であることが，その次の図を見るとわかります．

■さて，始めの半径１の円と，$$ｎ→∞$$回の爪切りで生じる円弧の円の中心は始めの円周上にあるという関係を繰り返して作図すると，以下図のような円の族が得られます．次々得られる円の大きさは，すぐ前の√2倍になっている美しいものです．確認してください．

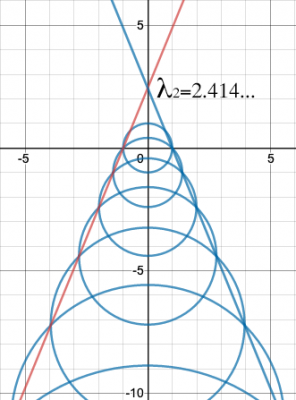
重なる円の交点は直線上に乗り，これらの2本の直線は$$y$$座標の2.414･･･の点で交わります．これはひとつ前の円の円周上の南極点を中心にし，$$√2$$倍に拡大された円の族に対しての結果です．
次に生じる円の中心は，前の円の円周上の南極点であるのは同じですが，続く円の大きさを$$A_{n}＝λ_{n}-(n-1)$$倍にすると，この円の族では，重なる円の交点を乗せる直線の交点は$$λ_{n}$$を与えます．確認ください．

 0
 0