━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 [2023.01.03] No.455
<<数学と社会の架け橋=数学月間>>
━━━━━━━━━━━━━━━━━━━━
2023年になりました。新年おめでとうございます。
今回のメルマガは、前回の続きで、数学者Edward Frenkel著の「愛と数学」-隠された現実の心 の紹介です。
歳を跨ぐ形になりましたが、この本の主張は、「数学者ではない一般の人に数学への共感を広げようという数学月間の趣旨」と一致します。
数学月間の考え方は、この本のどこに共感するのかをまとめてみましょう:
数学は、社会のあらゆる分野を支えて(いろいろな分野で登場します)いますが、一般の人は数学を嫌って避けようとします。
それは、数学が孤高で孤立しているからです。マーフィーの法則で、「言葉が通じなければそれは数学」と揶揄されたりします。
数学者は、出来上がった論理体系の数学を教えるだけでなく、相手のいろいろな分野に入り込みその分野の数学を組み立てて
見せる必要があります。数学科への数学があるように、工学、薬学、医学、経済、などにはそれぞれの数学があります。
ユークリッドやニュートン、ライプニッツの数学に留まらず、それ以降発展した数学分野をどんどん取り入れる必要があります。
定義、定理、証明の形式を軽視するものではありませんが、その繰り返しの簡潔な数学ではなく、その数学の適用分野や
その数学の発生現場も十分に言及してほしいと思います。
数学者には論理としての抽象的な数学が醍醐味でしょうが、一般の共感を得て普及するには、
数学は物理学の一部であると見た方が良いのです。この本の著者もそのように述べていたと思います。
前回の趣旨を数学月間流に解釈すると以上のようです。
次に、今回の趣旨を述べるのですが、素粒子の例がほとんどで冗長です。数学月間の会ホームページに移ってお読みください。
https://sgk2005.saloon.jp/bbses/bbs_articles/edit/232/d86e61800257d893cd1018ad509a8e1f?frame_id=328
https://sgk2005.saloon.jp/ は、年末にリホームしたいへん読み易くなりましたので、ぜひご訪問ください。
今回の部分の趣旨を一言で述べると、Edwardがなぜ数学を好きになったかが述べられています。
それは、優れた指導者に巡り合ったことから始まり、幸運な特殊なケースです。
素粒子物理に興味を持っていた子供が、良き数学指導者に会い、SU(3)群の学習へと導かれるわけです。
これは、Edwardの場合の例で、人によって必要とするものはそれぞれ異なり、数学のどの分野の話でもあり得ますので
これ以上の言及は避けます。
(注)SU(3)群とは、3次のユニタリー行列の作る群
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
第1章
どうやって数学者になるの?方法や手段はいろいろあると思います。これが私(Edward Frenkel)にどのように起こったかをお話ししましょう。
驚かれるかもしれませんが、学校では数学が嫌いでした。いいえ、「嫌われている」という言葉は強すぎるかもしれません。数学があまり好きではなかった。数学はつまらないと思いました。すべてのタスクを熱心に完了しましたが、なぜこれを行っているのかわかりませんでした。クラスで話し合った資料は、私には無意味で役に立たないように思えました。私は物理学、特に量子物理学に魅了されました。私は、この主題に関するすべてのノンフィクションの本をむさぼり食いました。私はロシアで育ちましたが、そのような文献を入手することは問題ではありませんでした。
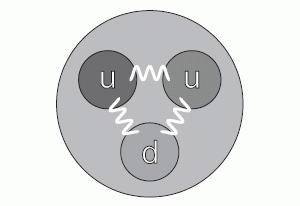
量子の世界に魅了されました!古代から、科学者や哲学者は、宇宙の基本的な性質を説明することを夢見てきました。すべての物質は原子と呼ばれる小さな粒子で構成されている。原子の存在は 20 世紀初頭に証明され、ほぼ同時期に、科学者は各原子がその構成要素に分解できることを発見しました。原子は原子核であり、その周りを電子が回っていることがわかりました。原子核自体は、図のように陽子と中性子からできています。
-----------略-------------------
ゲルマンによれば、クォークには「アップ」と「ダウン」の 2 種類があります。中性子と陽子は、アップ クォークとダウン クォークのさまざまな組み合わせによって形成されます。中性子は 2 つのダウン クォークと 1 つのアップ クォークで構成され (図 1.2)、陽子は 2 つのアップ クォークと 1 つのダウン クォークで構成されます (図 1.3)。
図1.3.陽子のクォーク構造
これはすべて非常に明確でした。しかし、陽子と中性子が不可分の粒子ではなく、さらに小さな粒子で構成されていることを物理学者がどのように推測できたのかは、私には謎のままでした。
1950 年代後半、科学者たちはハドロンと呼ばれる多数の素粒子を発見しました。中性子と陽子はハドロンのクラスに属し、物質の構成要素であり、日常生活で大きな役割を果たしています。残りのハドロンについては、その目的は明らかではありませんでした。科学者たちは、それらが何のためにあるのか(または、研究者の一人が言ったように、「誰がそれらを注文したのか」)をまったく理解していませんでした。宇宙には非常に多くの種類のハドロンが存在するため、影響力のある物理学者であるヴォルフガング パウリは、物理学が植物学に変わりつつあると冗談を言ったことさえあります。科学者たちは、ハドロンの分類に秩序をもたらし、ハドロンの振る舞いを支配し、この驚異的な多様性を説明できる根底にある原理を突き止めようと必死に努力しました。
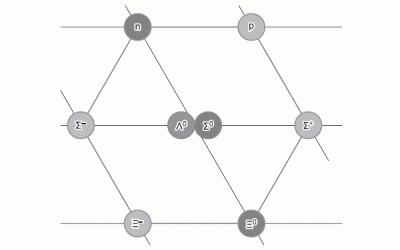
ゲルマンと独立したユヴァル・ネーマンは、素粒子の革新的な分類を提案しました。どちらも、ハドロンが自然に小さなファミリーに分類され、それぞれが 8 ~ 10 個の粒子であることを示しました。これらのファミリは、オクテットおよびデキュプレットと呼ばれます。同じファミリーに属する粒子は、似たような性質を持っています。
私が当時好きだった人気の本では、オクテットは図を使って描かれていました (図 1.4)。
図1.4.オクテッドのダイアグラム
図では、陽子はp + (プラス記号は正の電荷を示す)、中性子はn 0 (ゼロはこの粒子が電荷を持たないことを意味する) で表され、ギリシャ文字の奇妙な名前を持つ残りの 6 つの粒子があります。
しかし、なぜ 7 と 11 ではなく、8 と 10 の粒子なのでしょうか? 私が自由に使える本では、この現象の首尾一貫した説明を見つけることができませんでした。それは、ゲルマンによって開発された神秘的な理論に言及しています - ある種の「八正道」(仏教の聖なる八正道に似ています)。しかし、この理論が何であるかはどこにも述べられていませんでした。
この誤解は私を悲しくさせました。物語の重要な部分は、私の目から隠されたままでした。この謎を解明したかったのですが、方法がわかりませんでした。
幸いなことに、私たちの家族の古くからの友人から助けがありました。私は約 15 万人が住むコロムナという小さな工業都市で育ちました。コロムナはモスクワから約 115 キロ、電車で 2 時間強の場所にあります。私の両親は大規模な重工作機械工場でエンジニアとして働いていました。
コロムナは、2 つの川の合流地点に建設された古代都市です。それは1177年に設立されました(モスクワの設立からわずか30年後)。コロムナの建築遺産にはいくつかの美しい古い教会があり、コロムナ クレムリンの壁は今でも過去の歴史を思い起こさせます。しかし、コロムナは教育的または知的センターとは言えません。当時、市内には学校の教師を養成する小さな研究所が 1 つしかありませんでした。この教育機関の教授の 1 人である数学者の エフゲニー・エフゲニエビッチ・ペトロフは、私の両親の親友でした。ある日、母は通りで彼に会いました。彼らは長い間お互いに会っていなかったので、当然のことながら、彼らには多くの話題がありました。ママはいつも友達に私のことを話すのが好きだったので、彼らも私を無視して会話をすることはありませんでした。科学に興味があると聞いて、
- 私は彼に会わなければなりません。それを数学に置き換えてみます。
母は反対しました。彼は量子物理学を勉強したいと思っています。
「心配しないで」とエフゲニー・エフゲニエビッチは答えた。
彼らは会うことに同意した。私はあまり楽観的ではありませんでしたが、それでもエフゲニー・エフゲニエビッチと一緒に仕事をしました。
私はもうすぐ 15 歳になり、最後から 2 番目の 9 年生を終えようとしていました (1 年生をスキップしたため、クラスメートより 1 歳年下でした)。40代のエフゲニー・エフゲニエビッチは、フレンドリーで気取らない人物の印象を与えました。眼鏡をかけて無精ひげを生やした彼は、数学者という私の考えを具現化したものでしたが、彼の大きく開いた目の鑑定的な表情には、すぐに注目を集める何かがありました。彼らは好奇心を放ちました-彼は彼の周りで起こったことすべてに興味を持っていました。
エフゲニー・エフゲニエビッチは私を数学信仰に改宗させる狡猾な計画を本当に持っていました。私が彼のオフィスに入るとすぐに、彼は次の質問で私を驚かせました。
— 量子物理学が好きだと聞きました。ゲルマンの八正道とクォークモデルについて聞いたことがありますか?
はい、私はいくつかのポピュラー本で読んだことがあります.
しかし、このモデルが何に基づいているか知っていますか?
科学者はどのようにしてこれらのアイデアを思いつきましたか?
SU (3)群って何か知っていますか?
SU (3) 群に精通していない場合、どのようにクォークモデルを理解できますか?
*****************訳者注)*************
SU(3)群とは3次のユニタリー行列の作る群です。2次の行列が,パウリの4つの行列の線形結合で表現できるように,3次のユニタリー行列は8つのゲルマン行列の線形結合で表現できます。ここで登場する8という数字はSU(3)を生成する 8 つのゲルマン行列とかかわっています。
*****************************************
彼は本棚から数冊の本を取り出し、それらを開き、数式で満たされたページを見せてくれました。上記のようなおなじみのオクテット図に気付きましたが、それらは単なる美しい写真ではありませんでした。図は、一貫性のある詳細なプレゼンテーションの一部でした。
もちろん、式自体は何も理解していませんでしたが、これらのページで、私を真剣に悩ませていた質問への答えを見つけることができることがすぐにわかりました。気づきの瞬間でした。公式と言葉に魅了され、言葉では言い表せない、これまでなじみのない感覚に襲われました。エネルギー、インスピレーションが沸き起こるのを感じました。これは、音楽を聴いたり、なじみのない写真を見たりして、印象に残っているときに感じる方法です。「うわー!」という一つの考えが頭の中で渦巻いていた。
- 数学は学校で教えてくれるものだと思っていたでしょう - エフゲニー・エフゲニエビッチは続けました。彼は頭を振った。「いいえ、ここです」と彼は本の「真の数学」の公式を指さした。量子物理学を真に理解したい場合は、ここから始めるべきです。ゲルマンは美しい数学的理論でクォークの存在を予言しました。実際、それは数学的発見でした。
――でも、なかなか難しいですよね…。
式は本当に威圧的に見えました。
- 心配しないでください。最初に学ぶべきことは「対称群」です。ここからすべてが始まります。数学や理論物理学の大部分は、この概念に基づいています。私はあなたにいくつかの教科書をあげます。それらを読み始め、理解できない文に印を付けます。週に一度、あなたと会って、読んだ内容について話し合うことができます。
彼は私に対称群に関する本と数冊の本をくれました。彼らは、いわゆるp -進数 (私たちが子供の頃からよく知っている通常の数とはまったく異なる数体系) とトポロジー (基本的な幾何学的形状の科学) について話しました。エフゲニー・エフゲニエビッチは非の打ちどころのない趣味を持っていることが判明しました。彼はトピックの完璧な組み合わせを見つけたので、私はこの神秘的な怪物 -数学 -をまったく新しい視点から見て、恋に落ちました。
学校では、2次方程式、初歩の微分、基本的なユークリッド幾何学、三角法などを学びました。私には、すべての数学がどういうわけかこれを中心に展開しているように思えました-問題は時間の経過とともにより複雑になる可能性がありますが、それらは常に、私がすでに慣れ親しんでいるすべての同じ一般概念の枠組み内にとどまります。しかし、エフゲニー・エフゲニエビッチの本は、私にとってまったく異なる世界を開きました。
私はこの瞬間に転向しました。